应用回归分析(2)：一元线性回归

Oasis of the World

已于 2023-12-20 14:01:47 修改

阅读量1.7k

点赞数 3

分类专栏：应用回归分析及spss部分使用文章标签：回归 1024程序员节

于 2023-10-24 17:07:18 首次发布

本文链接：https://blog.csdn.net/qq_64279967/article/details/133764587

版权

应用回归分析及spss部分使用专栏收录该内容

6 篇文章 1 订阅

订阅专栏

2.1 回归模型

将两个变量通过一个线性方程联系起来。主要任务是：通过n组独立观测的数据对 $\beta_0,\beta_1$ 进行估计，得到一元线性经验回归方程： $\hat{y} = \hat{\beta_0} +\hat{\beta_1}x$

2.1.1 形式

$y = \beta _0 +\beta_1x +\varepsilon$

2.1.2 假设

1、因 $\varepsilon$ 不可观测，假设 $E(\varepsilon _i) = 0;var(\varepsilon _i)=\delta ^2;cov(\varepsilon_i, \varepsilon _j) = 0$ 。

2、n组数据时独立观测。

3、正态假设（在最大似然中和检验中用到）

2.1.3 结论

1、根据假设1两端求条件期望： $E(y|x)=E(y)=\beta _0 +\beta_1x$ ,这个称为（理论）回归方程

2、根据假设2： $y_1,y_2,y_3,.....,y_n$ 和 $\varepsilon _1 ,\varepsilon _2 ,...,\varepsilon _n$ 是相互独立的随机变量，而 $x_i$ 是确定性变量

3、根据结论2可得：对两端同时求期望和方差，得 $E(y_i) = \beta_0+\beta_1x;var(y_i)=\delta ^2$ 。表明 $y_1,y_2,...,y_n$ 的期望不相同，方差相等，因而 $y_1,y_2,...,y_n$ 是相互独立的随机变量但是不同分布。而 $\varepsilon _1 ,\varepsilon _2 ,...,\varepsilon _n$ 是独立同分布的随机向量！

4、根据结论3可得： $E(y_i) = \beta_0+\beta_1x$ 从平均意义上表达了变量y和x的统计规律性

2.1.4 不相关和独立

变量间的关系主要有互不相容、对立、独立和互不相关。
独立：有两随机事件 A、B 。 A、B 发生的概率分别为 P(A) 和 P(B) ， AB 事件同时发生的概率为 P(AB) 若 P(A)×P(B)=P(AB) ，则 A 与 B 相互独立。事件 A 发生的概率不影响事件 B 发生的概率，反应的是概率运算上的关系。
不相关：不相关是指两个变量的相关系数为0，两个变量之间没有线性关系的。

1.不相关是指的两个变量之间没有线性关系，并不一定没有其他关系。而独立指的是两个随机变量之间什么关系都没有。所以，独立一定不相关，不相关不一定独立。
2.特别的，当随机变量x,y是服从于二维正态分布时，不相关和独立等价！！！

原文链接：https://blog.csdn.net/qq_45126579/article/details/106397674

2.2 回归系数的估计

2.2.1 最小二乘法

（1）推导过程

[机器学习-回归算法]一元线性回归用最小二乘法的推导过程_一元线性回归最小二乘法推导-CSDN博客

（2）思想！！！！！

让残差的平方和SSE最小

（3）前提

$E(\varepsilon _i)=0; var(\varepsilon)=\delta ^2$

（4）结论

1、得到残差的性质： $\sum_{i=1}^{n}\varepsilon _i=0;\sum_{i=1}^{n}x_i\varepsilon _i=0$ ，即残差的平均值是0，残差以自变量 $x_i$ 的加权平均是0

2、

（5）最小二乘法的几何解释

详情见：（一文让你彻底搞懂最小二乘法（超详细推导）_最小二乘解-CSDN博客

通过图形可以看出， $a_1$ 和 $a_2$ 无论怎样组合不能得到 $b$ （不在同一个平面上/线性无关），这时无解，最小二乘法的含义是退而求其次的用距离 $b$ 最近的 $p$ 代替，这时求解 $Ax=p$ 。因为距离的最近： $\overrightarrow{e}$ 垂直于平面，因为： $\overrightarrow{e} = \overrightarrow{b}-Ax$ ,则 $a_1^T \cdot e = 0,a_2^T \cdot e = 0$ ,则写一起就是 $A^T(b-Ax)=0$ ,解出 $A^Tb=A^TAx \\x = (A^TA)^{-1}A^Tb$

2.2.2 最大似然估计

（1）推导过程

参考：

这时得到的 $\delta ^2$ 是有偏估计

（2）前提

1、最大似然估计是在 $\varepsilon _i \sim N(0,\delta ^2)$ ，且 $\varepsilon _i$ 相互独立！这个假设的前提下，但是最小二乘法无需要求

2、根据结论1的正态分布：随机变量 $y_i \sim N(\beta_0+\beta_1x_i,\delta ^2)$ 也服从正态分布

（3）结论

1、 $\beta _0,\beta_1$ 的结果与最小二乘法一样

2、得到 $\delta ^2$ 的有偏估计是: $\delta ^2= \frac{1}{n}\sum _{i=1}^{n}(y_i-\hat{y})^2$

3、 $\delta ^2$ 的无偏估计是: $\delta ^2= \frac{1}{n-2}\sum _{i=1}^{n}(y_i-\hat{y})^2$ ，注意在这里是n-2，但是在之前是n-1

关于之前方差的估计是n-1为分母的原因参考：为什么极大似然估计得到的方差是有偏估计_方差的极大似然估计-CSDN博客

关于现在的方差估计是n-2为分母的原因：

主要是 $y_i$ 的方差改变，将在以下部分进行阐述

2.3 最小二乘估计性质

一般讨论统计量的性质有以下几个维度：

（1）线性性

（2）无偏性

（3）方差

（4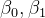） $\beta_0,\beta_1$ 协方差

！！！结论：

1、由方差可以得到的结论：x的取值尽量分散而且n尽量较大，这样估计值的稳定性会好

2、由协方差的式子可知： $\overline{x}=0$ 时， $\beta_0,\beta_1$ 不相关

3、高斯-马尔柯夫条件： $E(\varepsilon _i) = 0;var(\varepsilon _i)=\delta ^2;cov(\varepsilon_i, \varepsilon _j) = 0$ 。在此条件下可以证明出： $\hat{\beta_0},\hat{\beta_1}$ 分别时 $\beta_0,\beta_1$ 的最佳线性无偏估计（BLUE），也称为最小方差线性无偏估计。

4、对于固定的 $x_0$ 来说， $\hat{y_0}=\hat{\beta_0}+\hat{\beta_1}x_0$ 也是 $y_1,y_2,....,y_n$ 的线性组合，且 $\hat{y_0}\sim N(\beta_0+\beta_1x_0,(\frac{1}{n}+\frac{(x_0-\overline{x})^2}{L_{xx}})\delta ^2)$ ,由此可见 $\widehat{y_0}$ 是 $E(y_0)$ 的无偏估计。 $\widehat{y_0}$ 的波动和 $|x_0-\overline{x}|$ 有关，随着其增大而增大。这索命在实际应用回归方程进行控制和预测是，给定的 $x_0$ 不能离样本均值太远，否则用回归方程做因素分析和预测效果都不太理想。

2.4 回归方程显著性检验

常见的抽样分布：【Math】概率论常用分布大全 - 知乎 (zhihu.com)

样本方差服从卡方分布：概率统计笔记（十六）补1：样本方差服从卡方分布 - 知乎 (zhihu.com)

2.4.1 T检验

t检验构造：

2.4.2 F检验（判断方差齐性）

理论：

参考一文详解F检验 - 知乎 (zhihu.com)

对方差分析（ANOVA）的直观解释及计算 - 知乎 (zhihu.com)

之前学习的F检验在判断方差齐性：多个正态总体的均值是否相同

关于系数显著性检验的主要步骤如下：

2.2.3 相关系数的检验

一元线性回归方程讨论的是x,y之间的线性关系，所以可以通过相关系数检验回归方程的显著性。

（2）结论分析：r=0 只能说明没有线性关系但是不能说明没有关系

（3）缺点：相关系数接近1的程度和n的大小有关！当n较小时，相关系数的绝对值更容易接近1

特别是当n=2时，相关系数的绝对值等于1

2.2.4 三种检验之间的关系

对于一元线性回归来说，三种检验完全一样。（F检验是t检验的平方)

但是对于多元线性回归来说，三种检验表示的东西是不一样的！

2.2.5 决定系数（R方）

决定系数是反应回归直线和样本观测值拟合优度的相对指标。

在总离差平方和中回归平方和所占的比重越大，拟合效果越好。

所以： $r^2 = \frac{\sum _i^n (\widehat{y_i}-\overline{y})^2}{\sum _i^n (y_i-\overline{y})^2}$

其中 $r^2$ 正好是相关系数的 $r$ 的平方

2.5 残差分析

一个线性回归方程通过了t检验和f检验，只是表明变量x和y之间的线性关系是显著的，说明线性回归方程是有效的，但是不能保证数据拟合得很好！

2.5.1 残差的概念和残差图

残差 $e_i$ 可以看作是误差 $\varepsilon _i$ 的估计值， $e_i = y_i-\widehat{y_i}= y_i-\widehat{\beta_0}-\widehat{\beta_1}x_i$ ; $\varepsilon _i = y_i-\beta _0-\beta _1x_i$

以自变量x为横坐标，（或以因变量或回归值 $\widehat{y}$ 做横轴），以残差作纵轴，将相应的残差点画在图像上就可以得到，残差图。

检验通过时：所有的残差应该在 $e=0$ 附近随机变化，并在变化幅度不大在一个区域里。

2.5.2 有关残差的性质

1、 $E(e_i)=0$

2、 $var(e_i) = [1-\frac{1}{n}-\frac{(x_i-\overline{x})^2}{L_{xx}}]\delta ^2=(1-h_{ii})\delta^2$ ,其中 $h_{ii} =\frac{1}{n}+\frac{(x_i-\overline{x})^2}{L_{xx}}$

3、 $\sum _{i=1}^{n} e_i = 0, \sum _{i=1}^{n}x_i e_i = 0$

2.5.3 改进的残差

残差分析中，一般认为超过 $\pm 2\delta ^2$ 或 $\pm 3\delta ^2$ 的残差为异常值，考录到普通残差的方差不等，做判断时带来一定麻烦，所以引入改进的方差

标准化残差： $ZRE_i = \frac{e_i}{\widehat{\delta }}$

学生化残差： $SRE_i = \frac{e_i}{\widehat{\delta }\sqrt{1-h_{ii}}}$ ，其中 $h_{ii} =\frac{1}{n}+\frac{(x_i-\overline{x})^2}{L_{xx}}$

标准化残差使残差具有可比性， $\left | ZRE_i \right |>3$ 的相应观测值为异常值！！，简化判定工作但是没有解决方差不等的问题。学生化残差进一步解决了这个问题，认为 $\left | SRE_i \right |>3$

2.6 回归系数的区间估计

区间估计的相应概念：数理统计第19讲（区间估计概念，枢轴量法） - 知乎 (zhihu.com)

看一看还没有看！！！！！！！！！！！

这个区间包含这个真实值的概率是 $1-\alpha$ ，构造是运用枢轴量(有确定分布的！)

根据： $\beta _1 \sim N(\beta _1,\frac{\widehat{\delta }}{L_{xx}})$ 和 $\frac{(n-2)\widehat{\delta ^2}}{\delta ^2} \sim \chi ^2(n-2)$

得到：

其中 $\beta _1$ 的置信度为 $1-\alpha$ 的区间估计是： $(\widehat{\beta _1}-t_{\alpha /2}\frac{\widehat{\delta }}{\sqrt{L_{xx}}},\widehat{\beta _1}+t_{\alpha /2}\frac{\widehat{\delta }}{\sqrt{L_{xx}}})$