函数的单调性与曲线的凹凸性

目录

函数的单调性的判定方法

例题：                                                         

 曲线的凹凸性与拐点：

 函数的拐点：

 总结：

---

函数的单调性的判定方法

 我们给出定理：

 我们给出证明：

例题：

                                                             

 

 

 

 曲线的凹凸性与拐点：

如图所示：

 

 

 我们可以发现，对于凹的函数的图像，他们的斜率是在增大的，对于凸的图像的斜率是在减小的。

一阶导数表示函数图像的斜率，二阶导数表示函数图像的斜率的变化率，当二阶导数大于0时，表示函数图像的斜率在增加，表示函数图像是凹的，当二阶导数小于0时，表示函数图像的斜率在减小，表示函数图像是凸的。

 我们进行证明：

 

 

 函数的拐点：

 如图所示，在x0左侧的图像是凸的，在x0右侧的图像是凹的，我们把函数经过这一点，凹凸性发生改变，这一点就叫做拐点。

所以，我们称：

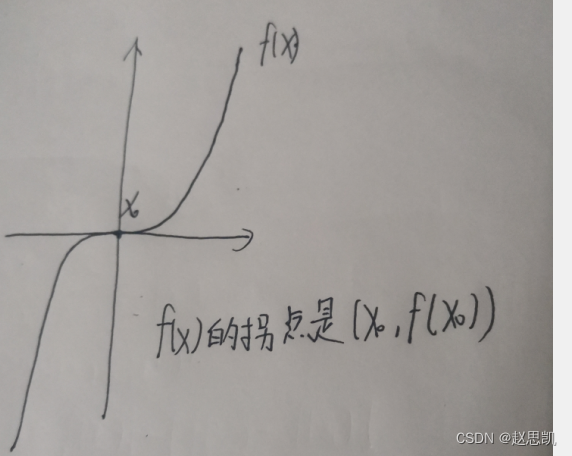
 我们发现，在这一点，函数的斜率的变化率为0，也就是说，函数的拐点对应的点的二阶导数为0.

函数的拐点对应的二阶导数为0，但是二阶导数为0的点并不一定是拐点。

例如：

 

 

 

 

 我们再举一个拐点的二阶导数不为0的点

 

 总结：