目录
4.2 基于Scikit-learn接口的XGBoost 二分类
一、 XGBoost简介
XGBoost(Extreme Gradient Boosting)是一种高效的梯度提升决策树算法,与lightgbm是目前表格型数据竞赛最主流的树模型。它在原有的GBDT(Gradient Boosting Decision Tree)基础上进行了改进,使得模型效果得到大大提升。XGBoost是由多棵CART(Classification And Regression Tree)组成,因此它不仅可以处理分类回归等问题。
XGBoost算法的核心是采用集成思想——Boosting思想,将多个弱学习器通过一定的方法整合为一个强学习器。它采用前向加法模型,用多棵树共同决策,每棵树的结果都是目标值与之前所有树的预测结果之差,并将所有的结果累加即得到最终的结果。这样可以大大提高整个模型的效果。
总之,XGBoost算法是一种基于梯度提升决策树的机器学习算法,具有高效、可扩展性、灵活性和鲁棒性等优点,被广泛应用于分类、回归、排序等任务中。
二、 XGBoost 数学原理
2.1 XGBoost 基本算法思想
XGBoost是boosting算法的其中一种。Boosting算法的思想是将许多弱分类器集成在一起形成一个强分类器。因为XGBoost是一种提升树模型,所以它是将许多树模型集成在一起,形成一个很强的分类器。该算法思想就是不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数,去拟合上次预测的残差。当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数,最后只需要将每棵树对应的分数加起来就是该样本的预测值。
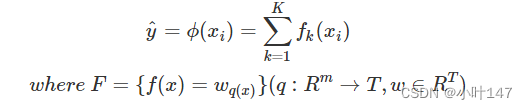
注:w_q(x)为叶子节点q的分数,f(x)为其中一棵回归树。
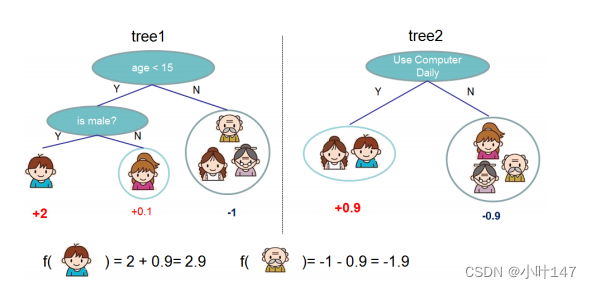
如下图例子,训练出了2棵决策树,小孩的预测分数就是两棵树中小孩所落到的结点的分数相加,爷爷的预测分数同理。
2.2 XGBoost 算法原理
2.2.1 XGBoost 预测原理
XGBoost是由 k个基模型组成的一个加法模型,假设我们第 t 次迭代要训练的树模型是ft(x) 则有:

2.2.2 XGBoost 目标函数

2.2.3 泰勒公式展开

2.2.4 定义基础树
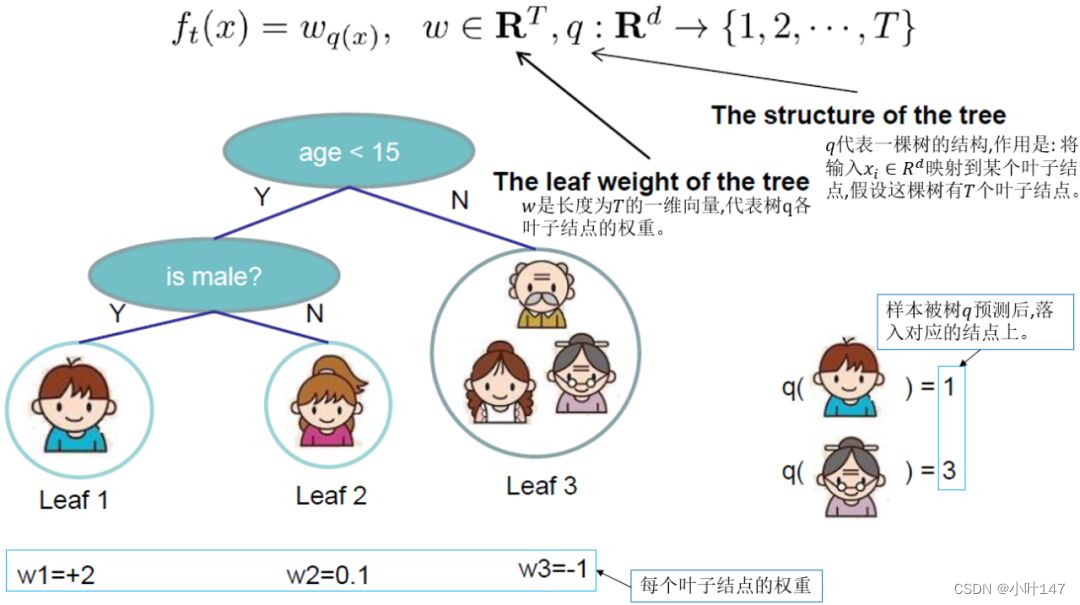
我们知道XGBoost的基模型不仅支持决策树,还支持线性模型,本文我们主要介绍基于决策树的目标函数。我们可以重新定义一棵决策树,其包括两个部分:
- L叶子结点的权重向量W ;
- 实例(样本)到叶子结点的映射关系q (本质是树的分支结构);
2.2.5 定义树的复杂度
决策树的复杂度 可由叶子数T组成,叶子节点越少模型越简单,此外叶子节点也不应该含有过高的权重
(类比 LR 的每个变量的权重),所以目标函数的正则项由生成的所有决策树的叶子节点数量,和所有节点权重所组成的向量的L2 范式共同决定。

2.2.6 叶子结点归组

2.2.7 树结构打分
回忆一下初中数学知识,假设有一个一元二次函数,形式如下:

我们可以套用一元二次函数的最值公式轻易地求出最值点:



上图给出目标函数计算的例子,求每个节点每个样本的一阶导数 gi和二阶导数hi,然后针对每个节点对所含样本求和得到Gi和Hi,最后遍历决策树的节点即可得到目标函数。
2.3 防止过拟合
XGBoost还提出了两种防止过拟合的方法:Shrinkage and Column Subsampling。Shrinkage方法就是在每次迭代中对树的每个叶子结点的分数乘上一个缩减权重η,这可以使得每一棵树的影响力不会太大,留下更大的空间给后面生成的树去优化模型。Column Subsampling类似于随机森林中的选取部分特征进行建树。其可分为两种,一种是按层随机采样,在对同一层内每个结点分裂之前,先随机选择一部分特征,然后只需要遍历这部分的特征,来确定最优的分割点。另一种是随机选择特征,则建树前随机选择一部分特征然后分裂就只遍历这些特征。一般情况下前者效果更好。
2.4 XGBoost 近似算法
对于连续型特征值,当样本数量非常大,该特征取值过多时,遍历所有取值会花费很多时间,且容易过拟合。因此XGBoost思想是对特征进行分桶,即找到l个划分点,将位于相邻分位点之间的样本分在一个桶中。在遍历该特征的时候,只需要遍历各个分位点,从而计算最优划分。从算法伪代码中该流程还可以分为两种,全局的近似是在新生成一棵树之前就对各个特征计算分位点并划分样本,之后在每次分裂过程中都采用近似划分,而局部近似就是在具体的某一次分裂节点的过程中采用近似算法。
三、 XGBoost 优缺点
3.1 优点
-
精度更高: GBDT 只用到一阶泰勒展开,而 XGBoost 对损失函数进行了二阶泰勒展开。XGBoost 引入二阶导一方面是为了增加精度,另一方面也是为了能够自定义损失函数,二阶泰勒展开可以近似大量损失函数;
-
灵活性更强: GBDT 以 CART 作为基分类器,XGBoost 不仅支持 CART 还支持线性分类器,使用线性分类器的 XGBoost 相当于带 L1和 L2正则化项的逻辑斯蒂回归(分类问题)或者线性回归(回归问题)。此外,XGBoost 工具支持自定义损失函数,只需函数支持一阶和二阶求导;
-
正则化: XGBoost 在目标函数中加入了正则项,用于控制模型的复杂度。正则项里包含了树的叶子节点个数、叶子节点权重的 范式。正则项降低了模型的方差,使学习出来的模型更加简单,有助于防止过拟合,这也是XGBoost优于传统GBDT的一个特性。
-
Shrinkage(缩减): 相当于学习速率。XGBoost 在进行完一次迭代后,会将叶子节点的权重乘上该系数,主要是为了削弱每棵树的影响,让后面有更大的学习空间。传统GBDT的实现也有学习速率;
-
列抽样: XGBoost 借鉴了随机森林的做法,支持列抽样,不仅能降低过拟合,还能减少计算。这也是XGBoost异于传统GBDT的一个特性;
-
缺失值处理: 对于特征的值有缺失的样本,XGBoost 采用的稀疏感知算法可以自动学习出它的分裂方向;
-
XGBoost工具支持并行: boosting不是一种串行的结构吗?怎么并行的?注意XGBoost的并行不是tree粒度的并行,XGBoost也是一次迭代完才能进行下一次迭代的(第 t 次迭代的代价函数里包含了前面 t-1 次迭代的预测值)。XGBoost的并行是在特征粒度上的。我们知道,决策树的学习最耗时的一个步骤就是对特征的值进行排序(因为要确定最佳分割点),XGBoost在训练之前,预先对数据进行了排序,然后保存为block结构,后面的迭代中重复地使用这个结构,大大减小计算量。这个block结构也使得并行成为了可能,在进行节点的分裂时,需要计算每个特征的增益,最终选增益最大的那个特征去做分裂,那么各个特征的增益计算就可以开多线程进行。
-
可并行的近似算法: 树节点在进行分裂时,我们需要计算每个特征的每个分割点对应的增益,即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下,贪心算法效率就会变得很低,所以XGBoost还提出了一种可并行的近似算法,用于高效地生成候选的分割点。
3.1 缺点
-
虽然利用预排序和近似算法可以降低寻找最佳分裂点的计算量,但在节点分裂过程中仍需要遍历数据集;
-
预排序过程的空间复杂度过高,不仅需要存储特征值,还需要存储特征对应样本的梯度统计值的索引,相当于消耗了两倍的内存。
四、 XGBoost 详细实现过程 (基于python)
4.1 安装XGBoost依赖包
pip install xgboostpip install sklearn4.2 基于Scikit-learn接口的XGBoost 二分类
实现XGBoost算法有两大接口,分别是XGBoost原生接口 和 scikit-learn接口,我比较常用 scikit-learn 接口,因此本文采用 scikit-learn 风格实现XGBoost二分类任务,由于鸢尾花数据集是一个多分类任务,这里为了实现更加简单,易懂,将多分类转化成二分类,具体实现过程及代码如下:
- 导入必要的库,包括Pandas、NumPy、load_iris函数从sklearn.datasets中导入鸢尾花数据集,以及XGBoost相关的库和一些评估和交叉验证的工具。
- 使用load_iris函数加载鸢尾花数据集,该数据包括特征和目标。
- 将数据和目标合并成一个DataFrame,并为列分配了新的名称(feat1、feat2、feat3、feat4和target)。
- 将多类分类问题转换为二分类问题,其中目标列target的值为2的实例被映射为1,其余的值保持不变,这将用于二元分类。
- 定义了特征列feature_cols,这些列将用于训练模型。
- 构建了一个XGBoost模型,并使用交叉验证进行训练。具体步骤包括:
- 定义了一组随机数种子(seeds)以用于不同的交叉验证折叠。
- 使用StratifiedKFold分层交叉验证将数据划分为若干折。
- 对每个折叠进行了训练和评估,打印了每个折叠的训练开始信息。
- 定义了XGBoost模型的超参数(xgb_params),如booster类型、目标、评估指标、树的深度、正则化参数等。
- 在每个折叠中,使用xgb.XGBClassifier训练XGBoost模型,使用早停策略并记录特征重要性。
- 评估模型的性能,计算准确度(accuracy_score)并打印。
#导入科学计算库
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
#导入机器学习库
import xgboost as xgb
from sklearn.model_selection import StratifiedKFold,KFold
from sklearn.metrics import accuracy_score
import warnings
warnings.filterwarnings('ignore')
# 读取尾花卉数据集
iris = load_iris()
#数据集合并
df_all = pd.concat([pd.DataFrame(iris.data),pd.DataFrame(iris.target)],axis=1,ignore_index=True)
df_all.columns=['feat1','feat2','feat3','feat4','target']
#转化为二分类问题
df_all['target'] = df_all['target'].apply(lambda x: 1 if x ==2 else x)
#训练特征
feature_cols=[col for col in df_all if col != 'target']
#构建模型
def xgb_model(train_x, train_y):
seeds=[512]
oof = np.zeros([train_x.shape[0],])
feat_imp_df = pd.DataFrame()
feat_imp_df['feature'] = train_x.columns
feat_imp_df['imp'] = 0
#5折交叉验证
for seed in seeds:
print('Seed:',seed)
folds = 5
kf = StratifiedKFold(n_splits=folds, shuffle=True, random_state=seed)
acc_scores = []
for i, (train_index, valid_index) in enumerate(kf.split(train_x, train_y)):
print("|-----------------------------------------|")
print("| XGB Fold {} Training Start |".format(str(i + 1)))
print("|-----------------------------------------|")
trn_x, trn_y, val_x, val_y = train_x.values[train_index], train_y.values[train_index], train_x.values[valid_index], \
train_y.values[valid_index]
xgb_params = {
'booster': 'gbtree',
'objective': 'binary:logistic',
'eval_metric': 'logloss',
'n_estimators':500,
'max_depth': 8,
'lambda': 10,
'subsample': 0.7,
'colsample_bytree': 0.8,
'colsample_bylevel': 0.7,
'eta': 0.1,
'tree_method': 'hist',
'seed': seed,
'nthread': 16
}
#训练模型
xgb_model = xgb.XGBClassifier(**xgb_params)
xgb_model.fit(trn_x,trn_y,eval_set=[(trn_x, trn_y),(val_x,val_y)],early_stopping_rounds=20,verbose=20)
#模型预测
val_pred = xgb_model.predict(val_x)
feat_imp_df['imp'] += xgb_model.feature_importances_ / folds/ len(seeds)
feat_imp_df = feat_imp_df.sort_values(by='imp', ascending=False).reset_index(drop=True)
feat_imp_df['rank'] = range(feat_imp_df.shape[0])
oof[valid_index] = val_pred / kf.n_splits / len(seeds)
#模型评价
acc_score = accuracy_score(val_y, val_pred)
print(acc_score)
acc_scores.append(acc_score)
print('AVG_acc:',sum(acc_scores)/len(acc_scores))
return oof,feat_imp_df
# 训练 XGB模型
xgb_oof, xgb_imp_df = xgb_model(df_all[feature_cols], df_all['target'])五、 XGBoost 参数详解
5.1 一般参数
n_estimators :n_estimators表示集成的弱评估器的个数,n_estimators越大,模型的学习能力就会越强,模型也越容易过拟合。 在随机森林中,调整的第一个参数就是n_estimators,这个参数非常强大,常常能够一次性将模型调整到极限。
booster:弱评估器,可以是gbtree,gblinear,dart,默认是gbtree
disable_default_eval_metric:是否禁用默认的(验证集的)评估指标,注意如果你要用自定义的评估指标,需要将这一项设为True
nthread:训练模型时用的并行线程数
verbosity:控制训练过程中输出信息的多少,取值为0, 1, 2, 3,默认为1
validate_parameters:是否检查参数
5.2 基学习器参数
基于树的弱评估器(gbtree, dart)的参数主要有以下几个:
eta:学习率,默认为0.3
gamma:叶节点继续分裂所需的最小损失函数下降值,默认为0,即不断增加树的深度直到损失函数不再下降
max_depth:树的最大深度,默认为6
min_child_weight:叶节点继续分裂所需的最小样本权重, 默认为1
subsample:训练样本的采样率,默认为1,即每次都用所有样本做提升
sampling_method:样本采样方法,默认为均匀采样
colsample_bytree, colsample_bylevel, colsample_bynode:特征采样率,colsample_bytree决定构建每一棵树的时候的采样率,colsample_bylevel决定树的深度每增加一层时的采样率,colsample_bynode决定每次叶节点分裂时的采样率,这三个参数默认都为1;在训练模型时三个参数的作用是累积的,例如数据共128个特征,colsample_bytree=colsample_bylevel=colsample_bynode=0.5,那么每个叶节点分裂时用到的特征数就是16
lambda:L2正则化系数,默认为1
alpha:L1正则化系数,默认为0
tree_method:构建树采用的算法,可选值有:auto, exact, approx, hist, gpu_hist,默认为auto
5.3 任务参数
objective:学习目标,默认为reg:squarederror,即以平方损失为损失函数的回归模型;除此之外还有:
| 参数 | 对应的学习目标 |
| reg:squaredlogerror | 以均方对数损失为损失函数的回归模型 |
| reg:logistic | 逻辑回归模型 |
| binary:logistic | 二分类逻辑回归模型(输出为概率,即Sigmoid函数值) |
| binary:logitraw | 二分类逻辑回归模型(输出为wTx,Sigmoid函数的参数) |
| binary:hinge | 使用合页损失函数(hinge loss)的二分类模型(输出为0或1) |
| multi:softmax | XGBoost采用softmax目标函数处理多分类问题,同时需要设置参数num_class(类别个数) |
| multi:softprob | 同softmax一样,只是输出为属于每个类别的概率 |
base_score:所有样本的初始偏置值,默认0.5
eval_metric:验证数据集的评估指标,对于回归问题,默认值是rmse,对于分类问题,默认是error,除此之外还有:
| 参数 | 对应的评估函数含义 |
| rmse | 均方根误差(∑Ni=1ϵ2N‾‾‾‾‾‾‾√) |
| mae | 平均绝对误差(∑Ni=1|ϵ|N) |
| logloss | 负对数似然函数值 |
| error | 二分类错误率(阈值为0.5) |
| merror | 多分类错误率 |
| mlogloss | 多分类logloss损失函数 |
| auc | 曲线下面积 |
seed:随机数种子(默认0),设置它可以复现随机数据的结果,也可以用于调整参数
5.4 训练参数
early_stopping_rounds:控制训练速度;如果在验证数据集上迭代early_stopping_rounds次后损失函数没有下降就停止训练;要求evals参数不能为空。
verbose_eval:控制评估模型过程中的输出数量,bool类型或int类型,默认为True,即每个提升阶段都输出相应信息;要求evals参数非空。
callbacks:回调函数(列表),在每轮迭代结束后调用
六、XGBoost 问题与思考
6.1 XGBoost与GBDT的联系和区别有哪些?
(1)GBDT是机器学习算法,XGBoost是该算法的工程实现。
(2)正则项: 在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。
(3)导数信息: GBDT在模型训练时只使用了代价函数的一阶导数信息,XGBoost对代价函数进行二阶泰勒展开,可以同时使用一阶和二阶导数。
(4)基分类器: 传统的GBDT采用CART作为基分类器,XGBoost支持多种类型的基分类器,比如线性分类器。
(5)子采样: 传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用了与随机森林相似的策略,支持对数据进行采样。
(6)缺失值处理: 传统GBDT没有设计对缺失值进行处理,XGBoost能够自动学习出缺失值的处理策略。
(7)并行化: 传统GBDT没有进行并行化设计,注意不是tree维度的并行,而是特征维度的并行。XGBoost预先将每个特征按特征值排好序,存储为块结构,分裂结点时可以采用多线程并行查找每个特征的最佳分割点,极大提升训练速度。
6.2 为什么XGBoost泰勒二阶展开后效果就比较好呢?
(1)从为什么会想到引入泰勒二阶的角度来说(可扩展性): XGBoost官网上有说,当目标函数是MSE时,展开是一阶项(残差)+二阶项的形式,而其它目标函数,如logistic loss的展开式就没有这样的形式。为了能有个统一的形式,所以采用泰勒展开来得到二阶项,这样就能把MSE推导的那套直接复用到其它自定义损失函数上。简短来说,就是为了统一损失函数求导的形式以支持自定义损失函数。至于为什么要在形式上与MSE统一?是因为MSE是最普遍且常用的损失函数,而且求导最容易,求导后的形式也十分简单。所以理论上只要损失函数形式与MSE统一了,那就只用推导MSE就好了。
(2)从二阶导本身的性质,也就是从为什么要用泰勒二阶展开的角度来说(精准性): 二阶信息本身就能让梯度收敛更快更准确。这一点在优化算法里的牛顿法中已经证实。可以简单认为一阶导指引梯度方向,二阶导指引梯度方向如何变化。简单来说,相对于GBDT的一阶泰勒展开,XGBoost采用二阶泰勒展开,可以更为精准的逼近真实的损失函数。
6.3 XGBoost对缺失值是怎么处理的?
在普通的GBDT策略中,对于缺失值的方法是先手动对缺失值进行填充,然后当做有值的特征进行处理,但是这样人工填充不一定准确,而且没有什么理论依据。而XGBoost采取的策略是先不处理那些值缺失的样本,采用那些有值的样本搞出分裂点,在遍历每个有值特征的时候,尝试将缺失样本划入左子树和右子树,选择使损失最优的值作为分裂点。
6.4 XGBoost为什么可以并行训练?
(1)XGBoost的并行,并不是说每棵树可以并行训练,XGBoost本质上仍然采用boosting思想,每棵树训练前需要等前面的树训练完成才能开始训练。
(2)XGBoost的并行,指的是特征维度的并行:在训练之前,每个特征按特征值对样本进行预排序,并存储为Block结构,在后面查找特征分割点时可以重复使用,而且特征已经被存储为一个个block结构,那么在寻找每个特征的最佳分割点时,可以利用多线程对每个block并行计算。
参考文献:
一文读懂XGBoost(含公式推导)_讲懂xgboost_one-莫烦的博客-CSDN博客
XGBoost算法梳理[通俗易懂]-腾讯云开发者社区-腾讯云 (tencent.com)























 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








