CGAN(Conditional GAN)和GAN的不同（原理版）

不知道取什么名字的Ag+

已于 2023-06-15 20:33:31 修改

阅读量1.6k

点赞数 2

分类专栏： Study 文章标签：生成对抗网络深度学习神经网络

于 2023-06-15 17:01:08 首次发布

本文链接：https://blog.csdn.net/qq_74179195/article/details/131031500

版权

Study 专栏收录该内容

1 篇文章

订阅专栏

一、前言

本文基于GAN(Generative Adversarial Nets)和CGAN(Conditional Generative Adversarial Nets)两篇论文来阐述二者的不同。

GAN有两篇论文，一篇是2014年发布在arXiv的(linking:https://arxiv.org/pdf/1406.2661.pdf)，另一篇稍微新一点，是发布在NeurIPS上的最终版本(linking:https://papers.nips.cc/paper_files/paper/2014/file/5ca3e9b122f61f8f06494c97b1afccf3-Paper.pdf)。这两个版本主要的区别就是两篇论文中Related work是不一样的，arXiv版本的Related work我感觉没有那么related，本文基于NeurIPS版本阐述。

~~（手机端好像点开会报错）~~

CGAN：linking:https://arxiv.org/pdf/1411.1784.pdf

二、为什么需要CGAN？

我们都知道GAN是生成对抗网络，可以生成各种图片，但问题就在它生成的图片有很多，也就是很宽泛，但有时候我们需要它生成特定的图片，比如在动物数据集中，我希望它生成猫的图片；0~9数字中，我希望生成9这个数字，甚至是生成一串我输入的特定数字，比如1357。基于这个需求，CGAN应运而生。

那么GAN就从原来的无监督学习“摇身一变”，变成了监督学习CGAN。

而无监督学习和监督学习最大的不同就是，是否有标签（或者说，是否人为地告诉了模型一些规律），所以说，CGAN模型与GAN模型也没有什么不同嘛，不就多加了一个label。但是，就是这一个多了标签的不同，引起了很多东西的不同，落实到代码中去，也会有很多不一样的东西。

三、CGAN在GAN的基础上添加了什么？

（一）生成器G和判别器D的输入

we wish to condition on to both the generator and discriminator.

GAN中生成器G的输入只有噪声z，而在CGAN中生成器G的输入包含噪声z和标签y,也就是说，我们在输入一个noise时，还要额外告诉生成器，这个noise是什么标签的（限制生成器生成图像的范围），比如说，这个噪声是1，这个噪声是2，这个噪声是3，那么生成器就会根据y来生成图像。

判别器的输入是生成器生成的图像x和标签y(相较于GAN，也是多了一个标签y)。我的理解是，根据提供的标签y，判别器对图像x判别（判断图片x是来自真实的数据集图像还是合成的，大白话解释就是警察D要判断这个嫌疑人x是真的小偷还是悲惨的背锅侠）。

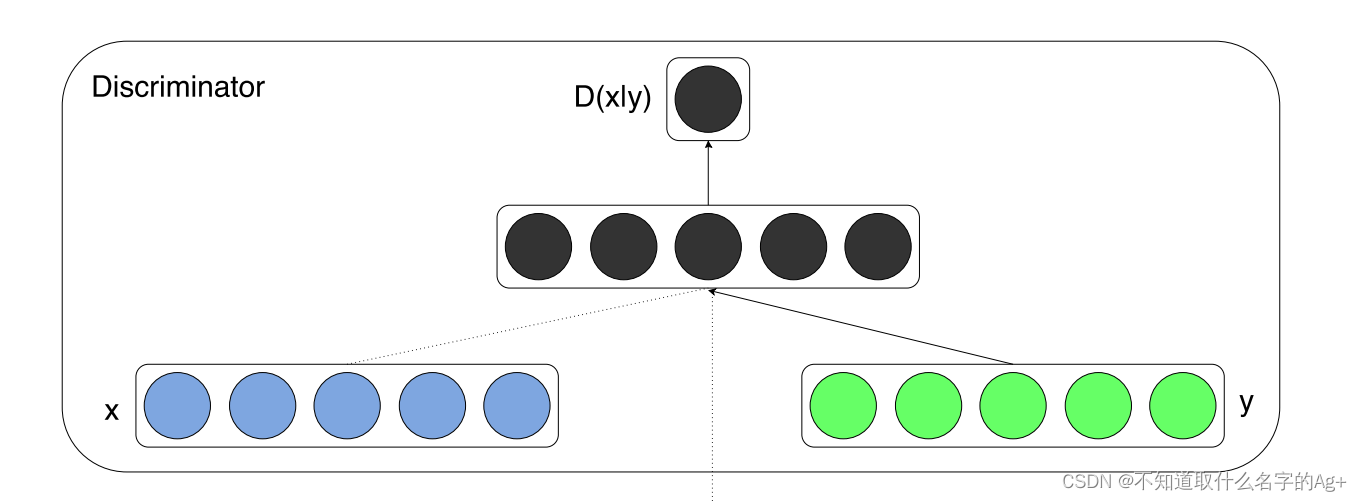
（二）那么标签怎么表示呢？

上文提到标签，可是计算机又看不懂我们人类的语言,那如何将我们的语言转换为计算机的语言？这就涉及到论文中所说的one-hot编码。

We trained a conditional adversarial net on MNIST images conditioned on their class labels, encoded as one-hot vectors.

One-hot Encoding:独热编码，又称一位有效编码，是数据预处理的方法之一。其方法是使用 N位状态寄存器来对 N个状态进行编码，每个状态都有它独立的寄存器位，并且在任意时候，其中只有一位有效。

(One-hot Encoding在NLP中更为常见)

比如数字，我用[1 0 0 0]表示1，[0 1 0 0]表示2，[0 0 1 0]表示3，[0 0 0 1]表示4，那么需要表示3124时，就会是这样一个矩阵（下图），可以利用pytorch中的one_hot()函数进行转换，由于该函数如无自己设定参数则默认以需要编码中的最大的数字（这里是4）+1作为编码长度（4+1=5），所以图片中的编码会比我们刚刚解释的多一列。

由于本文重点在GAN和CGAN上，所以不过多解释one-hot编码(one-hot是个神奇的东西，博大精深)。

（三）损失函数

GAN模型的损失函数是这样的：

而CGAN模型的损失函数是这样：

发现有什么不一样了吗？

log()内部的D(x)变成了D(x|y),D(G(Z))变成了D(G(z|y)，也就是从普通的概率变成了条件概率。

“条件”，可以理解为限制，我们将损失函数中的普通概率更换成条件概率，也就进一步缩小判断的范围，使得模型不仅是判断是真的图像还是生成的图像，还要判断这个图像是不是当前这个标签y的图像，从而达到conditional。

关于损失函数的理解：

随机掉落的碎片之损失函数不是越小越好吗，不是求最小值吗，为什么这里对G求min,对D求max?

Explanation:

首先，我们需要明确，判别器判断输入图像为真实图像，输出1；判断为生成的图像，则输出0。

（注意：虽然生成器和判别器是同时训练的，但是训练生成器时，函数中不含G的那部分为“常数”，我的表白对象不一样，关注的对象也就不一样，跟我们求偏导的道理是一样的。训练判别器时，同理。）

对于生成器G，它的目的就是骗过判别器D，也就是让判别器判断生成的图片为真实，输出为1。

（小偷要使劲提高自己的话术，让警察D以为他是好人。）

D(G(z|y))趋近1，那么函数中第二部分的log()内部也就趋近于0，对于log而言就是趋近于负无穷。此时由于表白对象是G，函数第一部分为常数，常数减去一个趋于负无穷的数，结果趋近负无穷。所以，想要G的效果越来越好，就要对G求min。

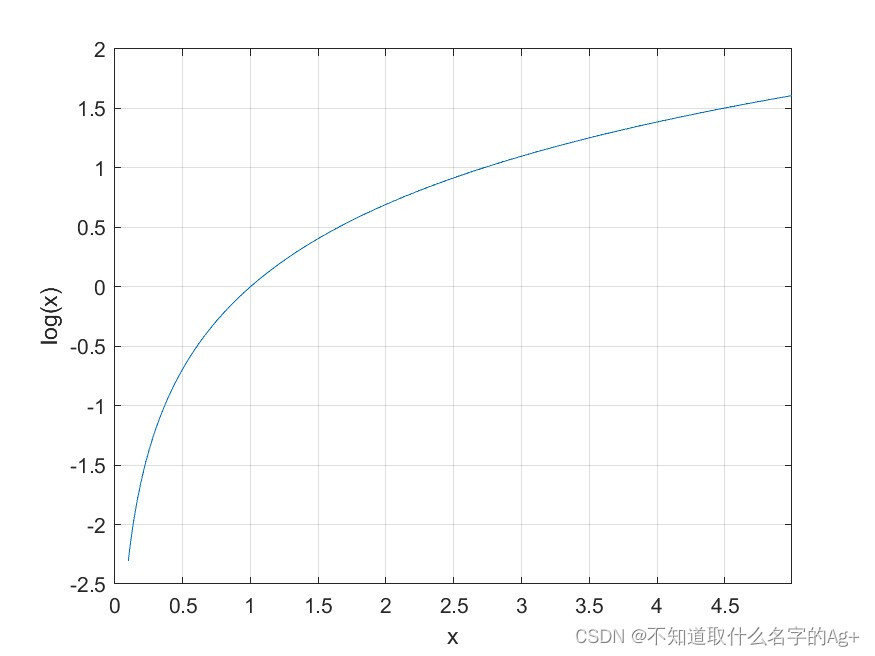
~~（趁机玩玩MATLAB）~~

对于判别器D，它的目的就是精确地判断出哪些图像是来自真实数据集的，哪些是来自生成器生成的。跟函数结合起来就是，D(x)要趋近1，D(G(z|y))要趋近0（真实的尽量判断为1，生成的尽量判断为0）。根据log函数的特点，D(x)趋近1，D(G(z|y))趋近0时，整个函数在X轴下方逐渐趋近0，也就是求max值。所以，判别器做得很好时，函数值应为0。

所以根据我们对损失函数的刻板印象，这个似乎不是损失函数，（所以作者在论文中称其为value function，但大家还是习惯模型一定有个损失函数），那我的理解，损失函数本质上是为了使模型效果更好，所以只要模型效果变好（overfitting另说），损失函数不一定是要减小的。

以上就是我在学习两个模型时的一些总结，欢迎大家评论区在评论区补充和指出不足之处，大家一起变得更强！

（以上图片除了l矩阵和og函数图片，其余均来自官方论文）