普林斯顿微积分(四) 如何求解涉及多项式的极限问题

---

前言

上一节，主要是从概念的角度学习了极限。
现在，是时候来看一看求解极限的技巧了。

---

4.1 包含当 x -> a 时的有理函数的极限

• 让我们以如下形式（有理函数）的极限开始： $\underset{x\to a}{\lim }\frac{p(x)}{q(x)}$
  • $p、q$ 都是多项式
  • $a$ 是一个有限的数

举例

代入

• 求 $\underset{x\to -1}{\lim }\frac{x^2-3x+2}{x-2}$
• 将 x = -1 代入，可得 $\frac{(-1{)}^2-3(-1)+2}{(-1)-2}=\frac{6}{-3}=-2$
• 因为其分母不为零，因此 -2 就是极限值

不定式

• 求 $\underset{x\to 2}{\lim }\frac{x^2-3x+2}{x-2}$
• 因为代入 x = 2 回将式子简化为 $\frac{0}{0}$，这被称作 不定式
• 使用代入法并得到零比零的形式，什么都可能发生：极限或许是有限的，极限或许是 ∞ 或 -∞，又或者，极限根本不存在。
• 这时，我们使用 因式分解
  • $\underset{x\to 2}{\lim }\frac{x^2-3x+2}{x-2}=\underset{x\to 2}{\lim }\frac{(x-2)(x-1)}{x-2}=\underset{x\to 2}{\lim }(x-1)$
  • 得到极限为 1

立方差公式

• $a^3-b^3=(a-b)(a^2+ab+b^2)$
• 求 $\underset{x\to 3}{\lim }\frac{x^3-27}{x^4-5x^3+6x^2}$
• 应用立方差公式 $\underset{x\to 3}{\lim }\frac{x^3-27}{x^4-5x^3+6x^2}=\underset{x\to 3}{\lim }\frac{(x-3)(x^2+3x+9)}{x^2(x-3)(x-2)}=\underset{x\to 3}{\lim }\frac{(x^2+3x+9)}{x^2(x-2)}=3$

分母为 0 但分子不为 0

• 不定式是形如 $\frac{0}{0}$，那如果分母为 0 但分子不为 0 会怎么样
• 在这种情况下，将总会涉及一条垂直渐近线
  • 即，有理函数的图像在你感兴趣的 x 值会有一条垂直渐近线
  • 但是会有四类行为出现

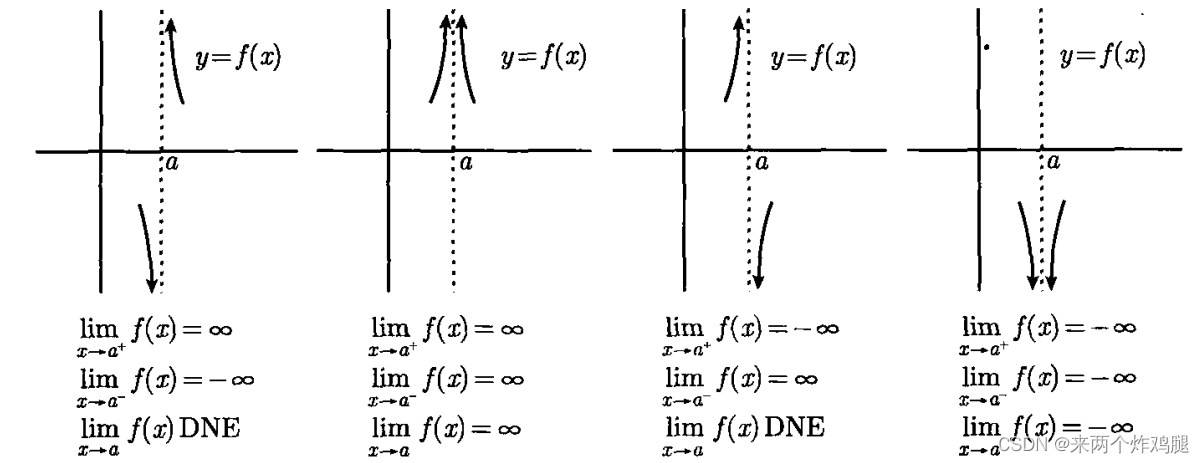
• 如何分辨出在处理这四种情形中的哪一种呢
  • 只需要查看一下 f(x) 在 x = a 两边的符号就可以了

举例

• 求 $\underset{x\to 1}{\lim }\frac{2x^2-x-6}{x(x-1{)}^3}$
• 我们指定 $f(x)=\frac{2x^2-x-6}{x(x-1{)}^3}$
• 并观察当移到 $x$ 到 $1$ 的附近时会有什么情况发生
  • 首先要注意的是，当 $x=1$ 时，分子 $f(x)=(2x^2-x-6)=-5$，因此，当在1的附近移动一下 x，它也保持为正的
  • 关键因子是 $x(x-1{)}^3$，当 $x>1$ 时为正，而当 $x<1$ 时为负
    • 即 $x>1\frac{(-)}{(+)\cdot (+)}=(-)$; $x<1\frac{(-)}{(+)\cdot (-)}=(+)$
• 所以符合上图中第三幅图
  • 可以看到双侧极限并不存在，而单侧极限存在

---

4.2 当 x -> a 时的涉及平方根的极限

举例

• 求 $\underset{x\to 5}{\lim }\frac{\sqrt{x^2-9}-4}{x-5}$
• 代入 $x=5$，得到 0/0 型的不定式，而进行因式分解好像不太管用
• 需要做的是，用 $\sqrt{x^2-9}+4$ 和分子相乘并相除，这被称作 $\sqrt{x^2-9}-4$ 的 共轭表达式
  • $\underset{x\to 5}{\lim }\frac{\sqrt{x^2-9}-4}{x-5}=\underset{x\to 5}{\lim }\frac{\sqrt{x^2-9}-4}{x-5}\times \frac{\sqrt{x^2-9}+4}{\sqrt{x^2-9}+4}=\underset{x\to 5}{\lim }\frac{x^2-25}{(x-5)(\sqrt{x^2-9}+4)}=\underset{x\to 5}{\lim }\frac{x+5}{(\sqrt{x^2-9}+4)}$
  • 现在就可以代入 $x=5$

---

4.3 当 x -> ∞ 时涉及的有理函数的极限

• 想求如下形式的极限： $\underset{x\to \infty }{\lim }\frac{p(x)}{q(x)}$

• 这有一个非常重要的多项式的性质： 当 x 很大时，首项决定一切

  • 也就是说，如果有一个多项式 $p$，那么，当 $x$ 变得越来越大时，$p(x)$ 的表现就好像只有它的首项存在一样
  • 设 $p_L(x$) 是 $p$ 的首项
    • 当 $x$ 变得非常非常大时， $\underset{x\to \infty }{\lim }\frac{p(x)}{p_L(x)}=1$

• 为了证明上式，需要一个定理： 对于任意的 $n>0$，只要 $C$ 是常数，就有 $\underset{x\to \infty }{\lim }\frac{C}{x^n}=0$

• 因此，当考虑极限 $\underset{x\to \infty }{\lim }\frac{p(x)}{q(x)}$

  • 如果 $p$ 的次数 = $q$ 的次数，则极限是有限的且非零
  • 如果 $p$ 的次数 > $q$ 的次数，则极限是 ∞ 或 -∞
  • 如果 $p$ 的次数 < $q$ 的次数，则极限是 0

---

4.4 当 x -> ∞ 时的多项式型函数的极限

• 考虑函数 $f$， $g$ ， $h$
  • $f(x)=x^3+4x^2-5x^{2/3}+1$
  • $g(x)=\sqrt{x^9-7x^2+2}$
  • $h(x)=x^4-\sqrt{x^3+\sqrt[5]{x^2-2x+3}}$
• 这些都不是多项式，因为它们含有分数次数或 n 次根，但是它们看起来有点像多项式
• 称它们为 多项式型函数

举例

第一种情况

• 求 $\underset{x\to \infty }{\lim }\frac{\sqrt{16x^4+8+3x}}{2x^2+6x+1}$
  • 分母是一个带有首项 $2x^2$ 的多项式，因此使用下式替换它
    • $\frac{2x^2+6x+1}{2x^2}\times (2x^2)$
  • 分子的首项为 $16x^4$，如果对其取平方根，会得到 $4x^2$，因此使用下式替换分子
    • $\frac{\sqrt{16x^4+8+3x}}{4x^2}\times (4x^2)$
• 把所有放在一起
  • $\underset{x\to \infty }{\lim }\frac{\sqrt{16x^4+8+3x}}{2x^2+6x+1}=\underset{x\to \infty }{\lim }\frac{\frac{\sqrt{16x^4+8+3x}}{4x^2}\times (4x^2)}{\frac{2x^2+6x+1}{2x^2}\times (2x^2)}$
  • $=\underset{x\to \infty }{\lim }\frac{\sqrt{\frac{16x^4+8}{16x^4}}+\frac{3x}{4x^2}}{\frac{2x^2+6x+1}{2x^2}}\times \frac{4x^2}{2x^2}=\underset{x\to \infty }{\lim }\frac{\sqrt{1+\frac{8}{16x^4}}+\frac{3}{4x}}{1+\frac{6}{2x}+\frac{1}{2x^2}}\times \frac{4}{2}=\frac{\sqrt{1+0}+0}{1+0+0}\times 2=2$

第二种情况

• 我们对上式稍加修改， 求 $\underset{x\to \infty }{\lim }\frac{\sqrt{16x^4+8}+3x^3}{2x^2+6x+1}$
  • 分母方法不变
  • 分子的首项为 $16x^4$，如果对其取平方根，会得到 $4x^2$，但是更高次数的项 $3x^3$ 将它淹没了
    • 因此必须使用下式替换分子
      • $\frac{\sqrt{16x^4+8}+3x^3}{3x^3}\times (3x^3)$
• 把所有放在一起
  • $\underset{x\to \infty }{\lim }\frac{\sqrt{16x^4+8}+3x^3}{2x^2+6x+1}=\underset{x\to \infty }{\lim }\frac{\frac{\sqrt{16x^4+8}+3x^3}{3x^3}\times (3x^3)}{\frac{2x^2+6x+1}{2x^2}\times (2x^2)}$
  • $=\underset{x\to \infty }{\lim }\frac{\sqrt{\frac{16x^4+8}{9x^6}}+\frac{3x^3}{3x^3}}{\frac{2x^2+6x+1}{2x^2}}\times \frac{3x^3}{2x^2}=\underset{x\to \infty }{\lim }\frac{\sqrt{\frac{16}{x^2}+\frac{8}{9x^6}}+1}{1+\frac{6}{2x}+\frac{1}{2x^2}}\times \frac{3x}{2}=\frac{\sqrt{0+0}+1}{1+0+0}\times \underset{x\to \infty }{\lim }\frac{3x}{2}=\infty$

第三种情况

• 如果多项式根和外面最高次项相等会怎样呢？
• 求 $\underset{x\to \infty }{\lim }\frac{\sqrt{4x^6-5x^5}-2x^3}{\sqrt[3]{27x^6+8x}}$
  • 分母还好，可是分子在平方根符号下，表现就像是首项 $\sqrt{4x^6}$，也就是 $2x^3$，但是后面也有一个 $-2x^3$，抵消之后好像就什么都没有了
  • 这里我们采用共轭表达式
    • $\underset{x\to \infty }{\lim }\frac{\sqrt{4x^6-5x^5}-2x^3}{\sqrt[3]{27x^6+8x}}=\underset{x\to \infty }{\lim }\frac{\sqrt{4x^6-5x^5}-2x^3}{\sqrt[3]{27x^6+8x}}\times \frac{\sqrt{4x^6-5x^5}-2x^3}{\sqrt{4x^6-5x^5}+2x^3}$

---

4.5 当 x -> -∞ 时的有理函数的极限

• 花点时间来看看形如： $\underset{x\to \infty }{\lim }\frac{p(x)}{q(x)}$ 的极限

• 之前使用的所有的原理在这里也使用

  • 当 x 是一个非常大的负数时，在任意和中的最高次数项仍然会占主导地位
  • 当 $x\to -\infty$ 时，只要 $C$ 是常数，并且 $n$ 是一个正整数， $C/x^n$ 仍然趋于 0

• 但有时候，只有在最后取极限的时候， $x\to \infty$ 和 $x\to -\infty$ 是不同的

• 还要注意，当 $x\to -\infty$ 时，$\sqrt{x^2}=-x$

• 即，如果 x < 0，并且想写 $\sqrt[n]{x^{\text{某}次幂}=x^m}$， 需要在 $x^m$ 之前加一个负号的唯一的情形是，当 $n$ 是偶的而 $m$ 是奇的

---

4.6 包含绝对值的极限

• 考虑： $\underset{x\to 0}{\lim }\frac{|x|}{x}$
• 设 $f(x)=|x|/x$
  • 首先，注意到 0 不可能在函数 $f$ 的定义域中
  • 当 $x$ 为正时，$|x|$ 这个量就是 $x$，$f(x)=1$
  • 另一方面，如果 $x$ 为负，那么 $|x|=-x$， $f(x)=-1$

• 因此，求左极限，需要从左侧接近 x = 0 ，有 $\underset{x\to 0^{-}}{\lim }\frac{|x|}{x}=-1$
• 同时， $\underset{x\to 0^{+}}{\lim }\frac{|x|}{x}=1$
• 由于左极限和右极限不相等，因此，双侧极限不存在，$\underset{x\to 0}{\lim }\frac{|x|}{x}$ DNE