对于优化算法的简单介绍

最新推荐文章于 2024-04-29 20:15:00 发布

rexyang97

最新推荐文章于 2024-04-29 20:15:00 发布

阅读量1.2k

点赞数 2

分类专栏：数学基础文章标签：算法

本文链接：https://blog.csdn.net/rexyang97/article/details/117815481

版权

数学基础专栏收录该内容

3 篇文章 0 订阅

订阅专栏

在平常的生活活着工作中，我们经常会遇到各种各样的最优化问题。比如每个企业和个人都要考虑的一个问题“在一定成本下，如何使利润最大化”，以及之前提到的下山，如何才能找到一条最短的路，使下山的时间最短。最优化方法是一种数学方法，它是研究在没有约束或者给定约束之下如何寻求某些因素(的量)，以使某一(或某些)指标达到最优的一些学科的总称。

优化问题一般可分为两大类：无约束优化问题和约束优化问题，约束优化问题又可分为含等式约束优化问题和含不等式约束优化问题。

1.无约束优化问题

2.含等式约束的优化问题

3.含不等式约束的优化问题

针对以上三种情形，各有不同的处理策略：

1.无约束的优化问题：可直接对其求导，并使其为0，这样便能得到最终的最优解。

2.含等式约束的优化问题：主要通过拉格朗日乘数法将含等式约束的优化问题转换成为无约束优化问题求解。

3.含有不等式约束的优化问题：主要通过KKT条件(Karush-Kuhn-Tucker Condition)将其转化成无约束优化问题求解。

无约束优化算法：

梯度下降法（Gradient Descent）：

梯度下降法是最早最简单，也是最为常用的最优化方法。就是之前提的下山问题，每一步都找出下山最快，即斜率最大的一条路走。对于多元函数，即用梯度。梯度下降法实现简单，当目标函数是凸函数时，梯度下降法的解是全局解。一般情况下，其解不保证是全局最优解，梯度下降法的速度也未必是最快的。梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向，因为该方向为当前位置的最快下降方向，所以也被称为是”最速下降法“。最速下降法越接近目标值，步长越小，前进越慢。

梯度下降法在靠近极小值时收敛速度会变慢，因为此时梯度可能会不够明显，而且容易陷入局部最优。例如你在下山使，最陡的那条路是通往山中的一个山谷的。而你到达山谷之后发现没有向下的路了，已经是最低点了。

而针对于这种会陷入局部最优的情况。后来提出了随机梯度下降法，即Stochastic Gradient Descent（SGD），它的基本思路与梯度下降法一样。不过每次计算时，只随机提取一部分训练样本进行计算，计算的结果运用在整体所有样本上，这样可以保证每次可能不会朝着下降最快的方向走，但整体方向还是大差不差的。SGD还有一个优点是计算量会较小，虽然可能迭代的次数会比原来多，但是每次迭代需要的计算量大大减小。

共轭梯度法（Conjugate Gradient）：

在上面的梯度下降法，我们会发现在某些情况下收敛的会很慢，即会走重复的路线，类似于螺旋下降或者“之”字路线。针对于这种情况便提出了共轭梯度法。共轭梯度法是在梯度下降法的基础上，每次计算下一次方向的时候的时候梯度与上一次进行改变的方向相结合。它仅需利用一阶导数信息，但克服了最速下降法收敛慢的缺点，又不需要存储和计算Hesse矩阵，共轭梯度法不仅是解决大型线性方程组最有用的方法之一，也是解大型非线性最优化最有效的算法之一。在各种优化算法中，共轭梯度法是非常重要的一种。其优点是所需存储量小，具有步收敛性，稳定性高，而且不需要任何外来参数。

具体的推导细节有兴趣的可以自己查阅https://en.wikipedia.org/wiki/Conjugate_gradient_method 本文就不细致描述了。

牛顿法与拟牛顿法：

原理是利用泰勒公式，在 $x_{0}$ 处展开，且展开到一阶, 即 $f(x)=f(x_{0})+f'(x_{0})(x-x_{0})$ 。求解方程 $f(x)=0$ ，等价于 $f(x_{0})+f'(x_{0})(x-x_{0})=0$ ，求解 $x_{1}=x_{0}-f(x_{0})/f'(x_{0})$ 。因为这是利用泰勒公式的一阶展开， $f(x)=f(x_{0})+f'(x_{0})(x-x_{0})$ 处并不是完全相等，而是近似相等，这里求得的 $x_{1}$ 并不能让 $f(x)=0$ ，只能说 $f(x_{1})$ 的值比 $f(x_{0})$ 的值更接近于0，于是迭代的想法就很自然了。

因为最小值是导数（梯度）为0的点，所以这里的f(x)=0其实指的是梯度为0，f'(x)就是二阶导，即Hessian矩阵。

从本质上看，梯度下降法是一阶收敛。牛顿法即是二阶收敛，比如下山问题中，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。所以一般牛顿法会收敛得更快。

而因为牛顿法的每一次迭代都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂。所以为了简化计算，便有了拟牛顿法。考虑用一个n阶矩阵 $B_{k}$ 来近似代替Hessian矩阵的逆矩阵。这就是拟牛顿法的基本想法。

我们尽可能地利用上一步的信息来选取 $B_{k}$ 。具体地，我们要求

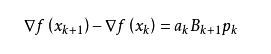
从而

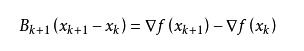
这个公式被称为割线方程。常用的拟牛顿法有DFP算法和BFGS算法。感兴趣的可以自己查阅

https://en.wikipedia.org/wiki/Quasi-Newton_method

约束优化算法：

关于拉格朗日乘数法在之前的数学基础章节中已经学习过了。主要就是在有约束即g(x)=0的情况下求多元函数方程式的极值。那么其实在最优化问题里我们也可以看做求多元函数方程式的极值，必定可以借助Lagrange乘子完成梯度合成，然后再使用牛顿法来迭代求解方程。

而拉格朗日乘子法适用于约束为g(x)=0的情况。针对于约束为不等式类似g(x)<=0的情况，便通过KKT条件解决。KKT条件通俗来说便是一种拉格朗日乘数法的泛华。对于优化问题：

$minf(x)$

$s.t.g_{j}(x)\leq 0$

$h_{k}(x)=0$

只需要满足于KKT条件，x*即为最优解：

$\left\{\begin{matrix} \frac{\partial f}{\partial x_{i}}+\sum_{k=1}^{l}\lambda _{k}\frac{\partial h_{k}}{\partial x_{i}}=0,(i=1,2...n) \\ h_{k}(x)=0 \\ \mu _{j}g _{j}(x)=0 \\ \mu _{j}\geq 0 \end{matrix}\right.$