“模式识别与机器学习”学习笔记no3.几种主要梯度下降方法的性能比较（一元函数求最值）

梯度下降方法是求目标函数最值的重要方法之一。借助它可以求解复杂的，超越的函数的优化问题。其主要思想在于，根据当前位置的梯度来决定下一步迭代的自变量取值，从而慢慢接近极小值。为了编程和计算的方便，本篇讨论在一元函数求最值背景下，几种梯度下降法的代码实现及性能比较。
Q：求函数$$x\ast cos(\pi \ast x/4)$$
的最小值。要求从x=-4开始迭代，迭代次数取50步。各超参数见代码。
参数设置及驱动程序：

import matplotlib.pyplot as plt
import numpy as np

# hyperparameters
iterations = 50
eta = 0.4  # initial learning rate
epsilon = 1e-6  # in case gradient==0
alpha = 0.9  # for RMSProp
lamda = 0.9  # for momentum
beta1 = 0.99  # for Adam
beta2 = 0.999

history_x = []
plot_x = np.linspace(-4.5, 4, 200)
plot_y = plot_x * np.cos(0.25 * np.pi * plot_x)
......
last_x, last_y = GradientDescent(-4)
print(last_x, last_y)
plt.show()
history_x.clear()
last_x, last_y = AdagradOptimization(-4)
print(last_x, last_y)
plt.show()
history_x.clear()
last_x, last_y = RMSPropOptimization(-4)
print(last_x, last_y)
plt.show()
history_x.clear()
last_x, last_y = MomentumOptimization(-4)
print(last_x, last_y)
plt.show()
history_x.clear()
last_x, last_y = AdamOptimization(-4)
print(last_x, last_y)
plt.show()

1.梯度下降法
参数更新公式：𝒘𝑡+1 ← 𝒘𝑡 − 𝜂∇𝐿𝑖𝑛(𝒘𝑡）
代码实现：

history_x.append(x)
    for i in range(0, iterations):
        x = x - eta * TargetFunctionGradient(x)
        history_x.append(x)
    print(history_x)
    plt.plot(plot_x, plot_y)
    plt.plot(np.array(history_x), TargetFunction(np.array(history_x)), markersize=3, color='r', marker='o')
    return x, TargetFunction(x)

除了给出最后停止时的x和函数值，也在图中标出迭代进行的轨迹。
表现：

2.Adagrad
自适应学习率，将在学习过程中根据梯度的大小来相应的调整学习率，使得算法在比较平滑的地方能够大踏步前进，在比较陡峭的地方能够放慢脚步，避免冲过极值点。
参数更新方式:

这里的epsilon是一个很小的正常数，用来避免分母为0.

def AdagradOptimization(x):
    history_x.append(x)
    sigma = TargetFunctionGradient(x) * TargetFunctionGradient(x)
    for i in range(0, iterations):
        x = x - eta / (np.sqrt(sigma / (i + 1)) + epsilon) * TargetFunctionGradient(x)
        sigma = sigma + TargetFunctionGradient(x) * TargetFunctionGradient(x)
        history_x.append(x)
    print(history_x)
    plt.plot(plot_x, plot_y)
    plt.plot(np.array(history_x), TargetFunction(np.array(history_x)), markersize=3, color='r', marker='o')
    return x, TargetFunction(x)

表现：

3.RMSProp
为了避免Adagrad学习率衰减太快的缺点而发明的改进版adagrad。均方根的引入可以减少学习率的摆动，更适合处理不平稳的目标模型，比adagrad更加常用。
参数更新方式:(这里只写出分母sigma更新的方式，可以比较其相对于adagrad更完善的地方)

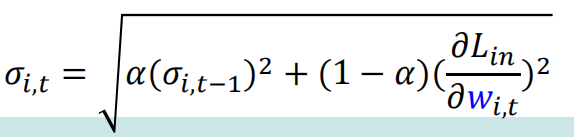
def RMSPropOptimization(x):
    history_x.append(x)
    sigma = TargetFunctionGradient(x) * TargetFunctionGradient(x)
    x = x - eta / np.sqrt(sigma) * TargetFunctionGradient(x)
    history_x.append(x)
    for i in range(1, iterations):
        sigma = alpha * sigma + (1 - alpha) * TargetFunctionGradient(x) * TargetFunctionGradient(x)
        x = x - eta / np.sqrt(sigma) * TargetFunctionGradient(x)
        history_x.append(x)
    print(history_x)
    plt.plot(plot_x, plot_y)
    plt.plot(np.array(history_x), TargetFunction(np.array(history_x)), markersize=3, color='r', marker='o')
    return x, TargetFunction(x)

表现：

这三种算法都没有脱离常规梯度下降法的形式，只是在学习率上想办法进行优化。可以发现adagrad在这道题的环境下用了更多的步骤，因为-4处梯度较大，一开始迭代进行的较慢。这个例子对于区分上面三种算法的优势效果不明显，但却非常明显的揭露了他们共同的劣势（这是由梯度下降法本身决定的)：会陷入局部极值而不能出来。无论选取哪种方法，在陷入局部极值或鞍点时，算法都不能提供足够的动力使迭代跳出局部极小，因为局部极小的梯度实在是太小了(分母的高阶无穷小)。动量法和adam法则提供了这种“动力”。
4.momentum法：
动量法，我认为更贴切的说法是“惯性法”。利用从山坡上冲下来的惯性，在达到局部极小的时候不停住，而是借助惯性冲上对侧的山坡，从而跳出局部极小，寻找可能的全局最小。
参数更新方式：

history_x.append(x)
    momentum = 0
    for i in range(0, iterations):
        momentum = lamda * momentum - eta * TargetFunctionGradient(x)
        x = x + momentum
        history_x.append(x)
    print(history_x)
    plt.plot(plot_x, plot_y)
    plt.plot(np.array(history_x), TargetFunction(np.array(history_x)), markersize=3, color='r', marker='o')
    return x, TargetFunction(x)

表现：

可以发现动量法冲过了第一个局部极小，并在全局最小附近发生了剧烈扰动，最后稳定在谷底。在这个例子中，动量法表现是最为优异的，但我认为他仍不是最优的优化方法。在图像的右半边扰动非常剧烈，如果函数的梯度不符合动量法的“胃口”，可能会带来无休止的往复扰动，无法继续向谷底进行迭代。但动量法为我们提供了冲出局部极小的可行思路，现在可以将前三种方法中表现最好的RMSProp法和动量法进行组合，得到一种强大的优化器。
5.Adam法
结合了RMSProp和Momentum两者之长。既用动量来累积“惯性”不至于陷入局部极小，又使得收敛速度更快同时使得波动的幅度更小（RMSProp的主要优点），并进行了偏差修正。参数更新过程比较复杂不好用少量的式子表示，直接上代码。

def AdamOptimization(x):
    m = 0
    v = 0
    history_x.append(x)
    for i in range(0, iterations):
        g = TargetFunctionGradient(x)
        m = beta1 * m + (1 - beta1) * g
        v = beta2 * v + (1 - beta2) * g * g
        m_hat = m / (1 - np.power(beta1, i + 1))
        v_hat = v / (1 - np.power(beta2, i + 1))
        x = x - alpha * m_hat / (np.sqrt(v_hat) + epsilon)
        history_x.append(x)
    print(history_x)
    plt.plot(plot_x, plot_y)
    plt.plot(np.array(history_x), TargetFunction(np.array(history_x)), markersize=3, color='r', marker='o')
    return x, TargetFunction(x)

表现：

迭代过程成功跳出局部极小（注意这里与momentum的不同，它已经十分接近局部极小的谷底，但是仍然几步冲出，体现了该算法对局部极小的优良抗性）。本例中它找出的最小值不如动量法，但在逼近最小值的迭代过程中显现了较强的稳定性，没有出现反复摆动的情况，做到了收敛速度快同时波动较小，总体上来说是相对最优的优化算法，在实际应用过程中也是使用最广泛的。但该算法牵扯到大量参数，想使该算法体现出最优性能，需要程序员进行大量的调参，十分依赖程序员的经验和耐心（我直接使用练习题提供的参数）。
总结：
该实验其实是模式识别与机器学习课的一道课后编程作业题，使得我们对几种算法的编写，调试，结果可视化有了动手操作的机会，体会了几种算法的异同和优劣。但该实验也存在不足，函数没有很好的体现出前三种算法的性能差异。（也是我做数据可视化的经验不足）
另一个不足是参数调试方面，为了我们的编程方便而直接给出了参数。当然后期可以对参数进行调整，这里不在展开。(注：笔者对迭代次数进行过一些调整，发现50次是整体表现比较好的，算法的各个参数调整之后在进行拓展研究)。