库存管理中的 (s, S) 策略，K convex，K 凸

当需求随机时，常见的库存管理中的订货策略有 (s, S) 策略：当库存水平低于或等于 s 时，订货到 S； 当库存水平高于 s 时，不订货。

若库存成本的递推函数是 k-凸，则 (s, S) 策略为最有订货策略，可以得到最小的期望总成本。

k-convex 的定义1：对于任何 x, 以及任何正数 a, b，满足如下条件：

\begin{equation}K+f(a+x)-f(x)-a\Big\{\frac{f(x)-f(x-b)}{b}\Big\}\geq 0\end{equation}

则为 k-convex.

或写为（定义2）：

\begin{equation}K+f(a+x)-f(x)-af'(x)\geq 0\end{equation}

或写为（定义3）：

\begin{equation}\mu f(x_1)+(1-\mu)(f(x_2)+K)\geq f(\mu x_1+(1-\mu)x_2)\end{equation}

证明 k-convex 要用到数学归纳法。

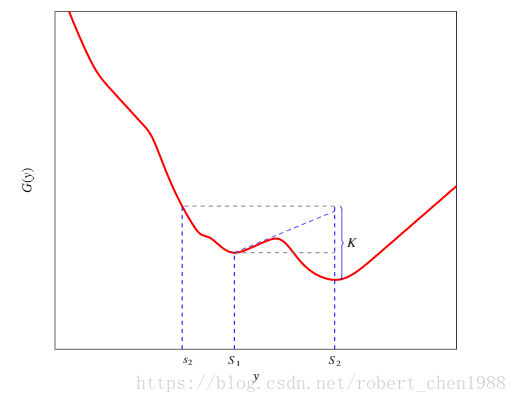
一个 K 凸函数的图形如下所示：

这个例子的各参数取值为：

% example: double fixedOrderingCost = 500; 
%      double proportionalOrderingCost = 0; 
%      double penaltyCost = 10;
%      double[] meanDemand = {9, 23, 53, 29}; //Poisson;
%      double holdingCost = 2;
%      int maxOrderQuantity = 100; 

个人认为：

K 凸函数的几何意义是，图形的波动不超过 K；

即任意两个点 x 与 x+a (a>0)， f(x) 与 f(x+a)+K 的连线一定高于 [x, x+a] 区域内的 f(x)图像。

下面的图形反映了定义2的几何意义：

下面的图形反映了定义1的几何意义：

猜想：两个 K 凸函数的最大值仍为 K 凸函数。