拉普拉斯变换/傅立叶变换/欧拉公式/泰勒级数的关联

背景：

这篇文章，就是整理看懂拉普拉斯变换需要用到的各种知识点，无它。

要看懂拉普拉斯变换，要先知道傅立叶变换，

要看懂傅立叶变换，要先知道复指数函数，

要看懂复指数函数，就先知道欧拉公式。

要看懂欧拉公式，就要先知道复指数函数的泰勒展开式。

要看懂复指数函数的泰勒展开式，就要先知道泰勒级数。

所以：

在了解拉普拉斯变换之前，先要了解欧拉公式，泰勒级数展开，指数函数的泰勒展开式。

知识从来不是孤立存在的，总有着千丝万缕的联系，这大概就是以点带面的含义吧。

泰勒级数：

指数函数泰勒展开：

按泰勒级数公式展开指数，所以：

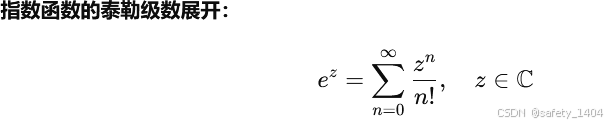
欧拉公式：

将复指数函数按泰勒级数展开，就能得到欧拉公式。

知道欧拉公式后，把θ换为ωt。变为，就能知道复指数函数为啥是连续的旋转运动了。

• ω 决定了旋转的快慢（频率）。单位是 弧度每秒（rad/s）。
• 如果 ω>0，向量逆时针旋转；如果 ω<0，则顺时针旋转

 复指数函数:

知道欧拉公式，再看复指数函数的形象表示如下图（注意横坐标、纵坐标的含义）：取不同的时间t，在复平面画出来，复指数最后表现出来的现象：就是一个连续旋转的圆，直径1，旋转的快慢就是w决定。

傅利叶变换：

先上公式，如下：

听的最多的就是：是自然界的很多函数曲线，都可以用三角函数进行分解。但是分解之后能干啥可能就不知道了。

傅立叶变换，就是把时间函数f(t)变成频率函数F(w)。就是横坐标由时间t，变成了w了(或者变成频率f，w=2πf)，从w的方向来看函数f(t)。

根据欧拉公式，复指数在复平面的表现形式是圆，加上时间轴，就成3维的，就是沿时间轴拉伸的螺旋线，旋转的快慢，就看频率大小。频率大，就旋转快，频率小就旋转的慢。

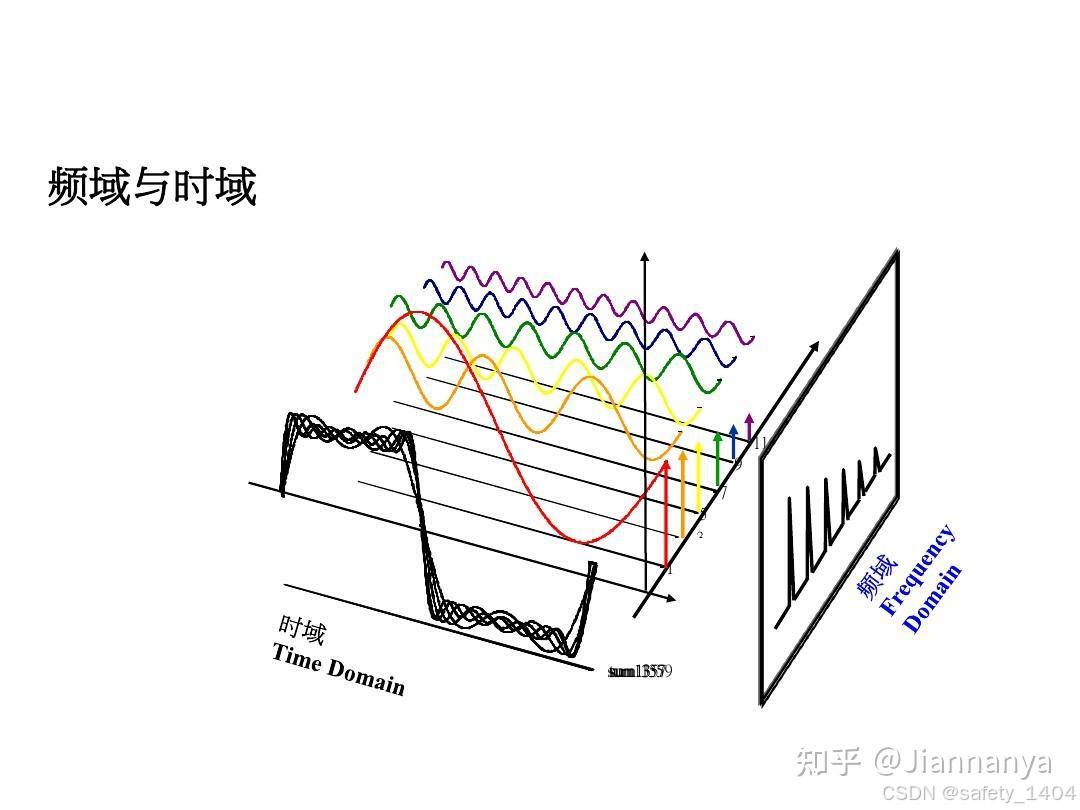
再看傅利叶变换公式。它就是有无数个这种不同旋转速度的螺旋组成的。只是，在不同的视角，你看的形状就不一样了，比如从上往下看，从左往右看，从右往左看这3个方向，在同一时刻，3个视角看到的图像肯定是不一样的。有无数个这个的螺旋。

想像一下，下图（频率域那个方向，省略了的螺旋，我不会画，画出来也会很乱，估计要动画才好看，只能靠想像了），频率域方向就是无数个螺旋（彩色曲线绕时间轴旋转，沿时间轴前进），在垂直时间轴这个侧面（左侧），看到的就是一条条正弦或余弦曲线。

从这里窃的一张图，里面有动画，便不是很完美，https://zhuanlan.zhihu.com/p/428783752

全部叠加后，就是我们看到一条函数曲线f(t)（图中最前面的黑色，一坨曲线，当然，实际我们只看到一条线，这里只是为了表示它是很多叠加的）。黑色背后的彩色曲线，就是傅立叶变换分分析出来的不同频率点的曲线。就是所谓的时域-频域转换。

既然有个傅立叶变换，可以用三角函数进行分解所有的函数，为啥还要拉普拉斯变换？因为这个结论不对，它不能分析所有的函数，只能对符合一定条件的函数才能进行傅立叶变换。不符合条件的就不行。拉普拉斯变换的本质意义（好文！通俗易懂）-CSDN博客

它要满足狗粮利赫里条件的函数，才可以用傅立叶转换，比如f(x）=x^2，就不满足第3个条件，就不能用傅立叶变换。

所以就有的拉普拉斯变换。

拉普拉斯变换

先上公式：

 是不是和傅立叶变换公式很像，但又说不出来，哪里不一样，对比一下。

至于拉普拉斯做了啥，可以再看这个文档，https://zhuanlan.zhihu.com/p/40783304有动画，形象一些。

总结来说就是：傅里叶变换有局限性，必须满足狄利赫里条件，特别是那个绝对可积的条件，一下子就拦截掉了一大批函数。比如函数f(x）=x^2 就无法进行傅里叶变换。聪明的数学家们，他们想到了一个绝佳的主意：把不满足绝对的可积的函数乘以一个快速衰减的函数，这样在趋于 时原函数也衰减到零了，从而满足绝对可积。

至于拉普拉斯变换用在什么地方，解决什么问题，可能还是不知道。