时间序列论文: NeuralProphet: Explainable Forecasting at Scale

mingo_敏

已于 2022-08-30 11:18:56 修改

阅读量2.1k

点赞数 2

分类专栏： TimeSeries Python 文章标签： python 人工智能 pandas

于 2022-08-24 09:47:45 首次发布

本文链接：https://blog.csdn.net/shanglianlm/article/details/126489531

版权

Python 同时被 2 个专栏收录

44 篇文章

订阅专栏

TimeSeries

13 篇文章

订阅专栏

时间序列论文: NeuralProphet: Explainable Forecasting at Scale
NeuralProphet之一：安装与使用
 NeuralProphet之二：季节性(Seasonality)
NeuralProphet之三：回归(Regressors)
NeuralProphet之四：事件(Events)
NeuralProphet之五：多时序预测模型
 NeuralProphet之六：多元时间序列预测
 NeuralProphet之七：NeuralProphet + Optuna
NeuralProphet之八：NeuralProphet部署
 NeuralProphet官方示例一：建筑物用电量预测(Building load forecasting)
NeuralProphet官方示例二：日照辐射强度预测(Forecasting hourly solar irradiance)

时间序列论文: NeuralProphet: Explainable Forecasting at Scale
NeuralProphet: Explainable Forecasting at Scale
PDF: https://arxiv.org/pdf/2111.15397.pdf
PyTorch代码: https://github.com/shanglianlm0525/TimeSeries

1 概述

NeuralProphet是一个基于PyTorch实现的客户友好型时间序列预测工具，延续了2018年Facebook开源预测工具Prophet的主要功能，主要用于时序数据分析（个人使用体验：最好是具备显著时序特征的数据）。NeuralProphet是在一个完全模块化的架构中开发的，这使得它可以在未来增加额外组件，可扩展性很强。项目意在保留Prophet的原始特性，如Classic AR模型可解释性、可配置性，并使用了PyTorch后台进行优化，如Gradient Descent，另外还引入了AR-Net建模时间序列自相关、自己设置损失和指标、具备前馈神经网络的可配置非线性层等等特性。

2 NeuralProphet

NeuralProphet是一个可分解的时间序列模型，和Prophet相比，类似的组成部分有趋势(trend)、季节性(seasonality)、自回归(auto-regression)、特殊事件(special events)，不同之处在于引入了未来回归项(future regressors)和滞后回归项(lagged regressors)。

未来回归项（future-known regressors）是指在预测期有已知未来值的外部变量，而滞后回归项（lagged covariates）是指那些只有观察期值的外部变量。趋势trend可以通过设置变化点来建立线性或者组合多个线性趋势的模型。季节性seasonality使用傅里叶项建模，因而可以解决高频率数据的多种季节性。自回归项（auto-regression）使用AR-Net的实现来解决，这是一个用于时间序列的自回归前馈神经网络(Auto-Regressive Feed-Forward Neural Network)。滞后回归项也使用单独的前馈神经网络进行建模。未来回归项和特殊事件都是作为模型的协变量，只要要single weight进行建模。

2-1 Model Components

NeuralProphet模型模型由多个模块组成，每个模块都有各自的输入和建模过程。每个模块都有自己的个人输入和建模过程。但是，所有模块都必须产生 h 个输出，其中h 定义了一次预测未来的步数。
在这里插入图片描述
其中：
T(t) = 时间 t 的趋势
S(t) = 时间 t 的季节性影响
E(t) = 时间 t 的事件和假日效应
F(t) = 未来已知外生变量在时间 t 的回归效应
A(t) = 基于过去观察的时间 t 的自回归效应
L(t) = t 时刻外生变量滞后观测的回归效应

所有模型组件模块都可以单独配置和组合以组成模型。如果所有模块都关闭，则仅安装一个静态偏移参数作为趋势分量。默认情况下，仅激活 trend 和 seasonality 模块。

2-1-1 Trend

建模趋势的经典方法是将其建模为偏移量 m 和增长率 k。 t1 时刻的趋势效应由增长率乘以从偏移量 m 顶部的起点 t0 开始的时间差。
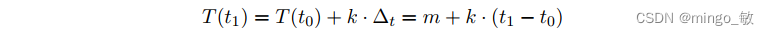
在这里插入图片描述

2-1-2 Seasonality

类似Prophet，NeuralProphet也使用傅立叶项（Fourier terms）来处理Seasonality。傅立叶项定义为正弦、余弦对并允许对多个季节性以及具有非整数周期的季节性进行建模。每个季节性可以定义为多个傅里叶项。
在这里插入图片描述
其中 k 具有周期性p的季节性的傅立叶的数量。每一个季节性对应 2k 个系数。在 t 时刻，模型涉及的所有季节性效应可以表示为：

每个季节周期性可以单独表示为 additive 或者 multiplicative 的形式：

NeuralProphet根据数据频率和长度自动激活每日、每周或每年的季节性。既周期大于2个季节性，激活对应季节性。默认每个季节性的傅立叶项数为：年：k=6，p=365.25，周： k=3，p=7，日：p=1，k=6。

2-1-3 Auto-Regression

Auto-regression (AR) 主要根据历史值来预测将来的值。经典的AR 模型可以表示为：
在这里插入图片描述
其中系数 $θ_{i}$ 控制特定的历史值 $y_{i-1}$ 的方向和幅度， $c$ 是常数， $e_{t}$ 为白噪声项， $p$ 为历史值个数。
当预测范围（forecast horizon）h大于1，滞后p 个历史值时，

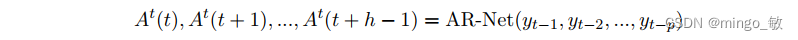
**AR order：**历史值的长度p，通常设置为最内周期或者预测范围两倍。

2-1-4 Lagged Regressors

滞后回归用于为我们的时间序列预测目标加入其他观察变量。在 t 时刻，我们只知道t-1时刻（包括t-1）前的观察值。
在这里插入图片描述

2-1-5 Future Regressors

对于future regressors，在t时刻，过去和未来的回归因子（regressor）都是知道的。
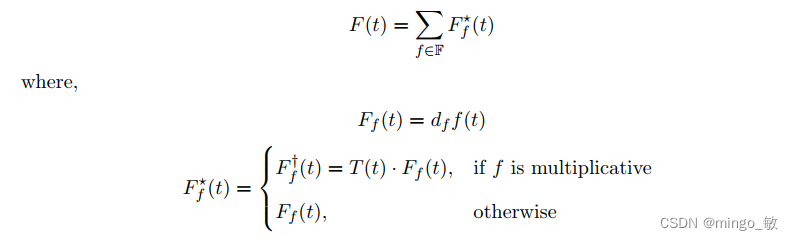
在这里插入图片描述

2-1-6 Events and Holidays

特殊事件或假日的影响可能偶尔发生。每个事件 $e$ 建模为一个二值变量 $\in [0, 1]$ , 表示事件在某天是否存在。对于一系列长度为 $T$ 和数量为 $n_{e}$ ，在时间 $t$ 时刻 , 所有事件的影响可以表示为 $E (t)$
在这里插入图片描述
其中 $z_{e}$ 为对应于事件 $e$ 的系数。
NeuralProphet可以建模两种类型的事件：1)用户定义; 2) 指定国家。对于指定的日期 $t_{e}$ ，前后 $i + j$ 天的时间窗口 $t_{e}−i, t_{e}+j]$ 也可以设定为特定事件。如Christmas可以通过设置 [−1, 0] 的时间窗口使得Christmas的前一天会对当前预测产生影响；

2-2 Preprocessing

2-2-1 Missing Data

当没有滞后变量的时候，直接丢掉缺失值就好。有滞后变量的情况下，每个缺失值会导致h + p被丢弃，因此引入数据插值机制；如果不特别指定的话，缺失值用 0 填充。
数据插值： 当Auto-regression 或者 lagged regressor使用的时候，主要采取三个步骤

1 对于不超过10个值的缺失，使用前后已知的值线性插值；
2 对于小于20个值的缺失，使用一个滑动窗口大小为30的计算平均值；
3 如果超过连续30个值缺失的话，不插值，直接丢弃这部分值；

2-2-2 Data Normalization

用户可以设定归一化的参数，如果不设定，对于二值化数值使用minmax，其他默认使用soft。
在这里插入图片描述

2-2-3 Tabularization

为了便于训练，时间序列数据表格化为一个伪独立且相同分布的数据集。

2-3 Training

Prophet 使用Stan 实现的 L-BFGS 拟合模型，NeuralProphet依赖PyTorch实现的SGD拟合模型；

2-3-1 Loss Function

NeuralProphet默认使用Huber loss，即smooth L1-loss，如下
在这里插入图片描述
对于给定的阈值 $β$ , 低于阈值 $β$ ，损失函数变为mean squared error (MSE)；高于阈值 $β$ ，损失函数变为mean absolute error (MAE)。用户可以设定MSE， MAE 或者其他PyTorch实现的函数；

2-3-2 Regularization

NeuralProphet使用权重绝对值的缩放和对数变换偏移作为一般正则化函数。
在这里插入图片描述
其中 $\epsilon \in (0, \infty )$ 为偏移的倒数， $\alpha \in (0, \infty )$ 为对数变换的比例。 $\epsilon$ 控制权重参数的稀疏程度， $\alpha$ 控制权重值的大小；

默认情况下，设置 $\epsilon =1$ ， $\alpha = 1$
在这里插入图片描述

2-3-3 Optimizer

默认使用AdamW

AdamW(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0.0001, maximize=False, capturable=False)

也可以选用SGD

SGD(params, lr=0.01, momentum=0.9, dampening=0, weight_decay=0.001, nesterov=False)

同时也可以使用PyTorch支持的其他 optimizer。

2-3-4 Learning Rate

通过测试的方式来估计一个学习率，针对特定的数据集大小，测试 $100 + l o g 10 (10 + T) * 50)$ 次, 测试区间从 $η = 1 e - 7$ 到 $η = 1 e + 2$ 之间。为了稳定性，分别测试三次求平均：
在这里插入图片描述

2-3-5 Batch Size

如果未指定，根据数据量T来决定，
在这里插入图片描述

2-3-6 Epochs

如果未指定，根据数据量T来决定，
在这里插入图片描述

2-3-7 Scheduler

采用’1cycle’ policy，学习率在最初的30%训练时间内从 $\frac{η}{100}$ 上升到 $η$ ，接着cosine曲线下降到 $\frac{η}{5000}$ ，直到训练结束。

2-4 Postprocessing

2-4-1 Metrics

可配置的metrics为RMSE,和 MAE，以及其他自定义的metrics。
在这里插入图片描述

2-4-2 Forecast Presentation

每次预测，model返回一个dataframe，每个dataframe包含一列预测的值，如 ’yhat3’ 表示基于三步前的数据为当前位置的预测值。

3 Data

https://github.com/ourownstory/neuralprophet-data
在这里插入图片描述