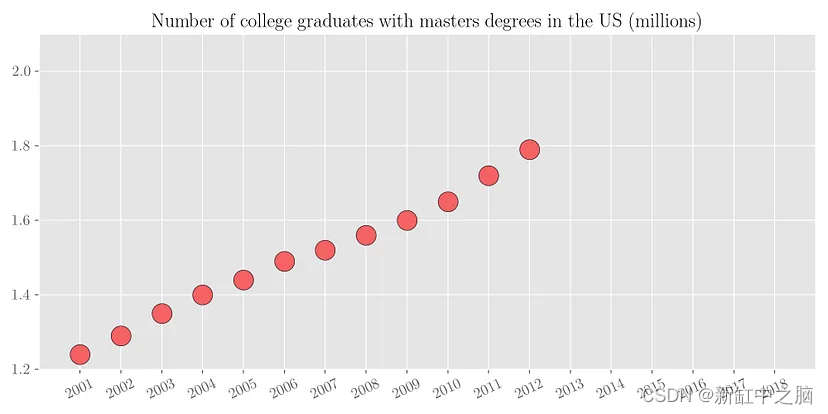
为了理解回归背后的动机,让我们考虑以下简单的例子。 下面的散点图显示了2001年至2012年美国大学毕业生的数量。
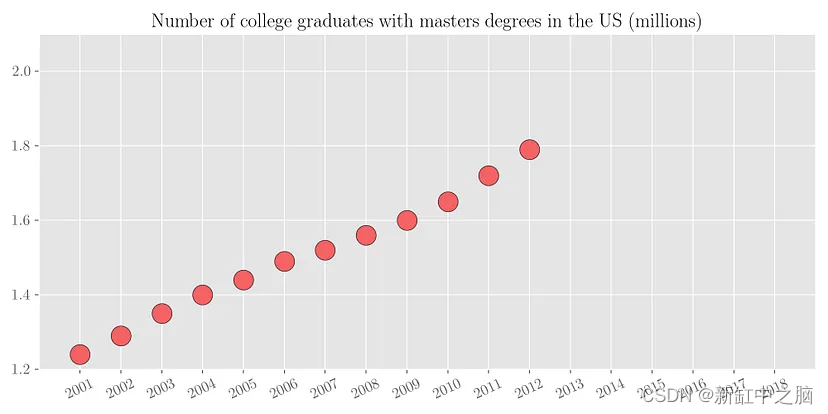
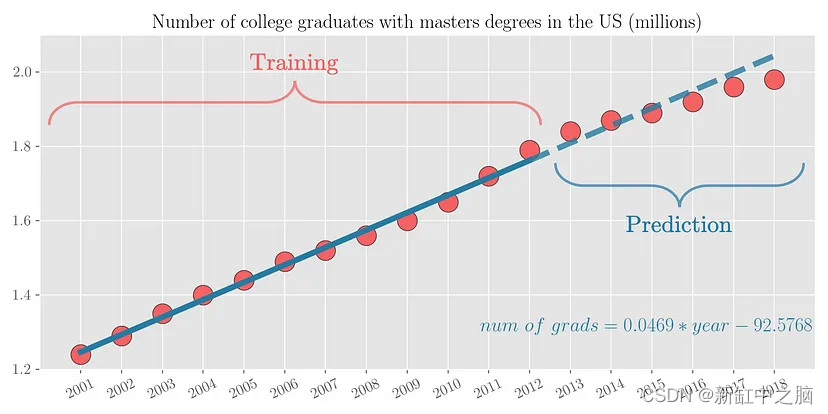
现在根据现有的数据,如果有人问你2018年有多少名大学毕业生获得硕士学位呢? 可以看出,具有硕士学位的大学毕业生数量几乎与年份呈线性增长。 因此,通过简单的视觉分析,我们可以粗略估计该数字在 200万 到 210 万之间。 我们来看看实际数字。 下图绘制了从 2001 年到 2018 年的同一变量。可以看出,我们的预测数字与实际值大致相符。
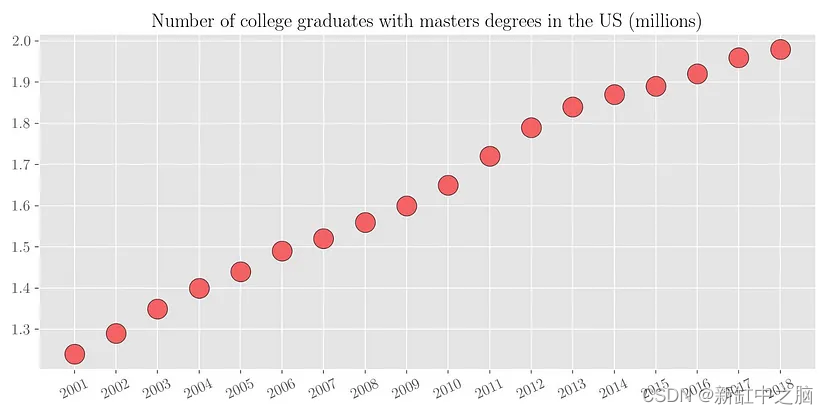
由于这是一个比较简单的问题(将一条线拟合到数据),我们的大脑很容易就能做到这一点。 这种将函数拟合到一组数据点的过程称为回归分析(regression analysis)。
1、什么是回归分析?
回归分析是估计因变量和自变量之间关系的过程。 简而言之,这意味着将选定函数族中的函数拟合到某个误差函数下的采样数据。 回归分析是机器学习领域用于预测的最基本工具之一。 使用回归,你可以在可用数据上拟合函数,并尝试预测未来或保留数据点的结果。 这种功能拟合有两个目的。
- 可以估计数据范围内的缺失数据(插值)
- 可以估计数据范围之外的未来数据(外推法)
回归分析的一些现实示例包括根据房屋特征预测房屋价格、预测 SAT/GRE 分数对大学录取的影响、根据输入参数预测销售、预测天气等。
让我们考虑一下前面大学毕业生的例子。
- 插值(interpolation):假设我们可以访问一些稀疏的数据,其中我们知道每 4 年大学毕业生的数量,如下面的散点图所示。
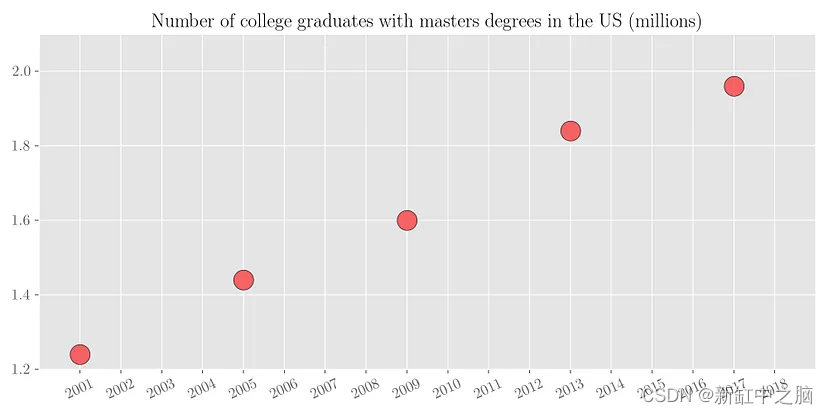
我们想要估计其间所有缺失年份的大学毕业生人数。 我们可以通过将一条线拟合到有限的可用数据点来做到这一点。 这个过程称为插值(interpolation)。
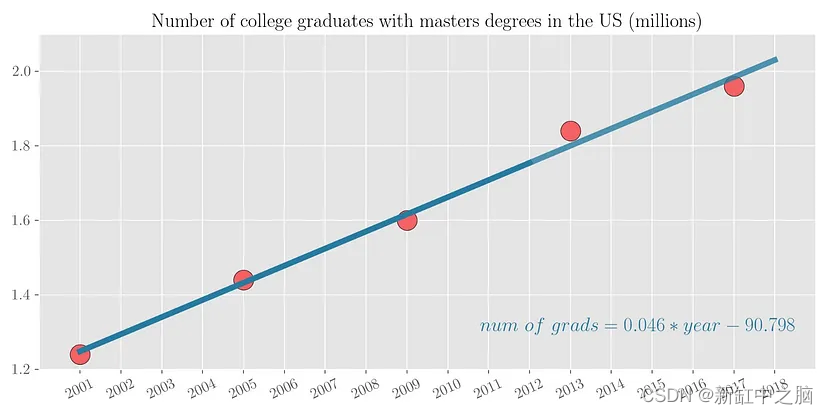
- 外推(extrapolation):假设我们只能获取 2001 年到 2012 年的有限数据,并且我们想要预测 2013 年到 2018 年的大学毕业生人数。
可以看出,具有硕士学位的大学毕业生数量几乎与年份呈线性增长。 因此,将一条线拟合到数据集中是有意义的。 用这12个点拟合一条线,然后在未来6个点上测试这条线的预测,可以看出预测非常接近。
用数学语言定义回归分析,就是用指定的数据点在一定的损失函数约束下估计某个函数的参数:
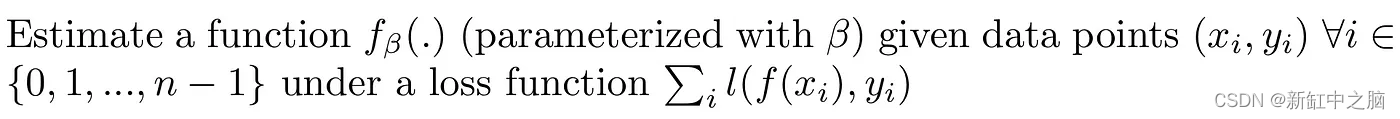
2、回归分析的类型
现在我们来谈谈进行回归的不同方法。 根据函数族 (f_beta) 和使用的损失函数 (l),我们可以将回归分为以下几类。
- 线性回归
- 多项式回归
- 岭回归
- Lasso回归
- ElasticNet回归
- 贝叶斯回归
- 逻辑回归
3、线性回归
在线性回归中,目标是通过最小化每个数据点的均方误差之和来拟合超平面(二维数据点的线)。
从数学上来说,线性回归解决了以下问题:
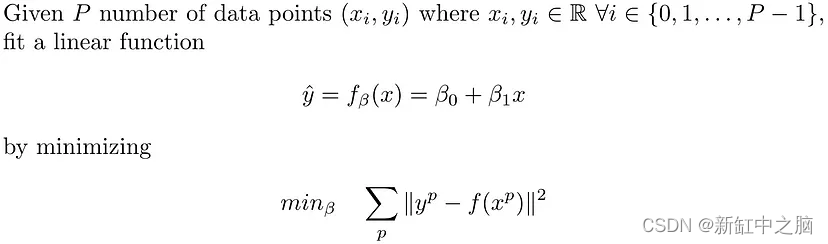
因此,我们需要找到 2 个用 beta 表示的变量来参数化线性函数 f(.)。 线性回归的示例如上图 4 所示,其中 P=5。 该图还显示了 beta_0 = -90.798 和 beta_1 = 0.046 的拟合线性函数
4、多项式回归
线性回归假设因变量 (y) 和自变量 (x) 之间的关系是线性的。 当数据点之间的关系不是线性时,它无法拟合数据点。 多项式回归通过将 m 次多项式拟合到数据点来扩展线性回归的拟合能力。 所考虑的函数越丰富,(一般来说)其拟合能力就越好。 从数学上来说,多项式回归解决了以下问题。
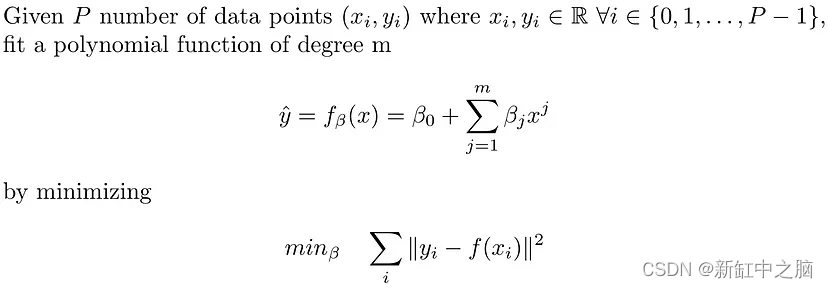
因此我们需要找到 (m+1) 个用 beta_0, …,beta_m 表示的变量。 可见,线性回归是2次多项式回归的特例。
考虑以下绘制为散点图的数据点集。 如果我们使用线性回归,我们得到的拟合显然无法估计数据点。 但如果我们使用 6 次多项式回归,我们会得到更好的拟合,如下所示:

[左] 数据散点图 — [中] 线性回归 — [右] 6 次多项式回归
由于数据点在因变量和自变量之间不存在线性关系,因此线性回归无法估计良好的拟合函数。 另一方面,多项式回归能够捕捉非线性关系。
5、岭回归
岭回归(Ridge Regression)解决了回归分析中的过度拟合问题。 要理解这一点,请考虑与上面相同的示例。 当25次多项式对10个训练点的数据进行拟合时,可以看到它完美地拟合了红色数据点(下中图)。 但这样做会损害中间的其他点(最后两个数据点之间的峰值)。 这可以从下图中看出。 岭回归试图解决这个问题。 它试图通过破坏训练点的拟合来最小化泛化误差。

[左] 数据散点图 — [中] 25 次多项式回归 — [右] 25 次多项式岭回归
从数学上来说,岭回归通过修改损失函数来解决以下问题:
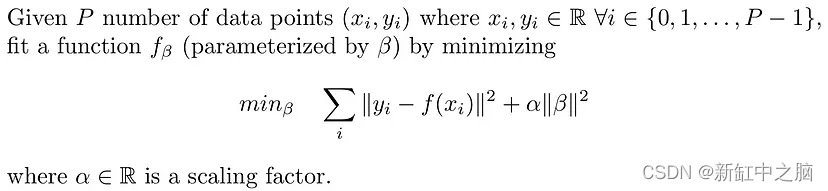
函数 f(x) 可以是线性函数或多项式函数。 在没有岭回归的情况下,当函数过度拟合数据点时,学习到的权重往往会相当高。 岭回归通过在损失函数中引入权重 (beta) 的缩放 L2 范数来限制所学习的权重范数,从而避免过度拟合。
因此,训练模型在完美拟合数据点(学习权重的大范数)和限制权重范数之间进行权衡。 缩放常数 alpha>0 用于控制这种权衡。 较小的 alpha 值将导致较高的范数权重并过度拟合训练数据点。 另一方面,较大的 alpha 值将导致函数与训练数据点拟合较差,但权重范数非常小。 仔细选择 alpha 值将产生最佳权衡。
6、LASSO回归
LASSO 回归与 Ridge 回归类似,因为它们都用作防止训练数据点过度拟合的正则化器。 但 LASSO 还有一个额外的好处。 它强制学习权重的稀疏性。
岭回归强制学习权重的范数变小,从而产生一组总范数减少的权重。 大多数权重(如果不是全部)将不为零。 另一方面,LASSO 试图通过使大部分权重接近于零来找到一组权重。 这会产生一个稀疏权重矩阵,其实现比非稀疏权重矩阵更加节能,同时在拟合数据点方面保持相似的精度。
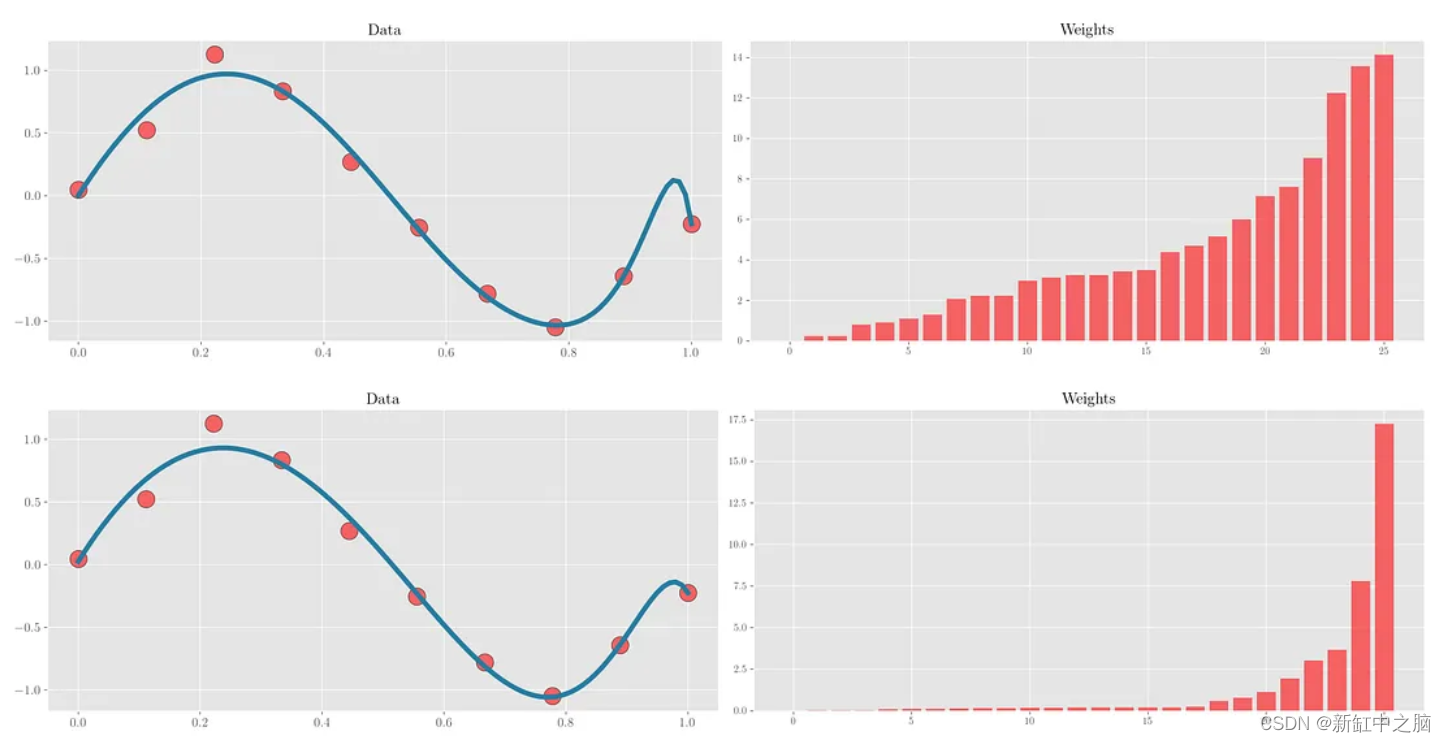
下图试图在与上面相同的示例中形象化这个想法。 使用 Ridge 和 Lasso 回归对数据点进行拟合,并按升序绘制相应的拟合和权重。 可以看出,LASSO回归中的大部分权重确实接近于零。
从数学上来说,LASSO回归通过修改损失函数来解决以下问题:
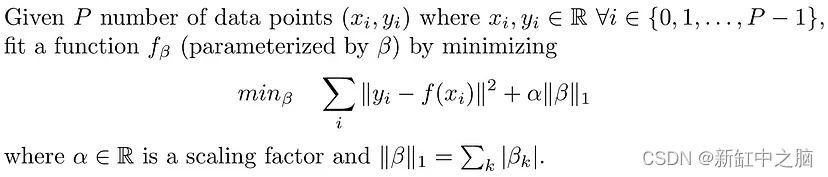
LASSO 和岭回归之间的区别在于 LASSO 使用权重的 L1 范数而不是 L2 范数。 损失函数中的 L1 范数往往会增加学习权重的稀疏性。 有关如何强制稀疏性的更多详细信息,请参阅这篇文章的 L1 正则化部分。
常数 alpha>0 用于控制学习权重的拟合度和稀疏度之间的权衡。 较大的 alpha 值会导致拟合效果不佳,但学习到的权重集会更稀疏。 另一方面,较小的 alpha 值会导致训练数据点紧密拟合(可能导致过度拟合),但权重集较少稀疏。
7、ElasticNet回归
ElasticNet 回归是 Ridge 回归和 LASSO 回归的组合。 损失项包括权重的 L1 和 L2 范数及其各自的缩放常数。 它通常用于解决 LASSO 回归的局限性,例如非凸性质。 ElasticNet 添加了权重的二次惩罚,使其主要是凸的。
从数学上来说,ElasticNet回归通过修改损失函数来解决以下问题:
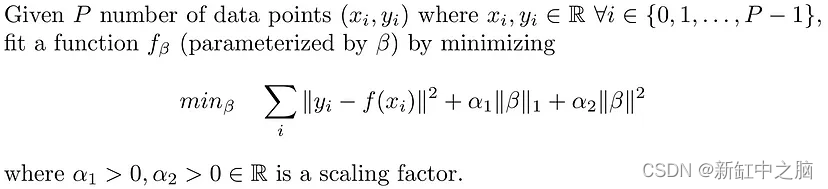
8、贝叶斯回归
对于上面讨论的回归(频率论方法),目标是找到一组解释数据的确定性权重值(β)。 在贝叶斯回归中,我们不是为每个权重找到一个值,而是尝试在假设先验的情况下找到这些权重的分布。
因此,我们从权重的初始分布开始,并根据数据,利用贝叶斯定理将先验分布与基于可能性和证据的后验分布联系起来,将分布推向正确的方向。
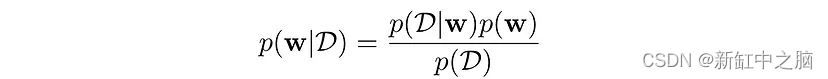
当我们有无限数据点时,权重的后验分布在普通最小二乘解的解中变成脉冲,即方差接近于零。
寻找权重分布而不是一组确定性值有两个目的
- 它自然地防止过度拟合的问题,因此充当正则化器
- 它提供了置信度和权重范围,这比仅返回一个值更具逻辑意义。
让我们用数学方式表述这个问题并给出它的解决方案:
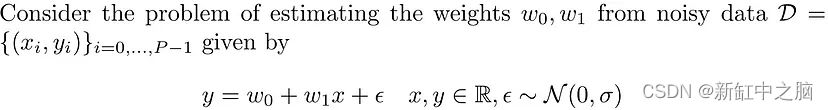
让我们对具有均值 μ 和协方差 Σ 的权重进行高斯先验,即:
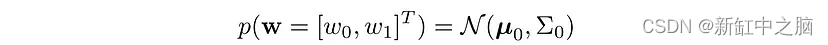
根据可用数据 D,我们更新此分布。 对于当前的问题,后验将是具有以下参数的高斯分布:
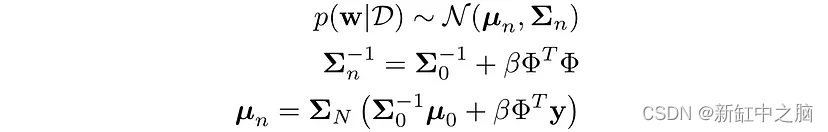
详细的数学解释可以在这里找到。
让我们通过每次更新一个数据点的权重分布来查看顺序贝叶斯线性回归,直观地尝试理解它。 如下图:
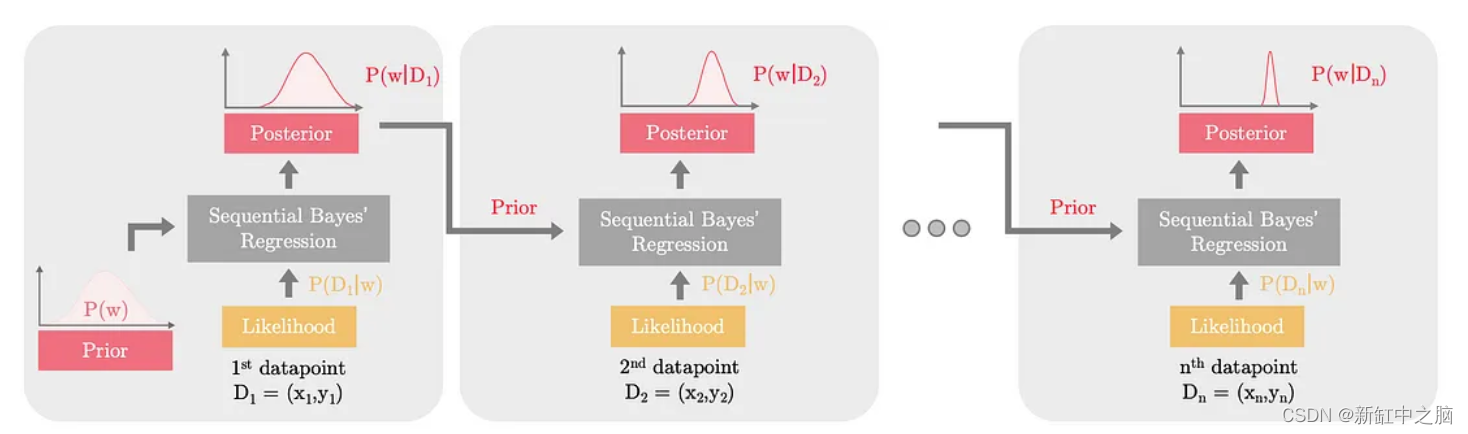
贝叶斯回归根据输入数据 (x, y) 将后验分布推向正确的方向
随着每个数据点的包含,权重的分布变得更接近实际的基础分布。
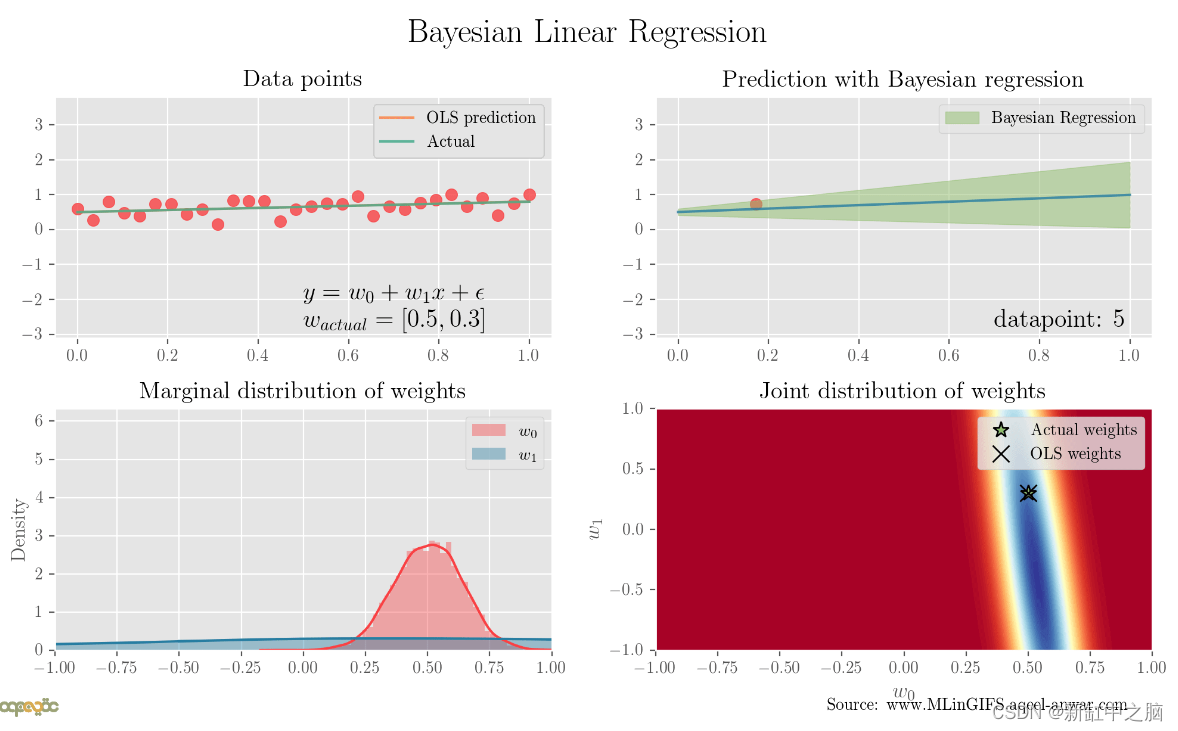
下面的动画绘制了考虑单个新数据点时每个时间步的原始数据、预测的四分位数范围、权重的边际后验分布以及权重的联合分布。 可以看出,随着包含的点越多,四分位数范围就越窄(绿色阴影区域),边际分布围绕两个权重参数分布,方差接近于零,并且联合分布收敛于实际权重。
9、逻辑回归
逻辑回归在分类任务中派上用场,其中输出需要是给定输入的输出的条件概率。 从数学上来说,逻辑回归解决了以下问题:

考虑以下示例,其中数据点属于两个类别之一:{0(红色),1(黄色)},如下面的散点图所示。
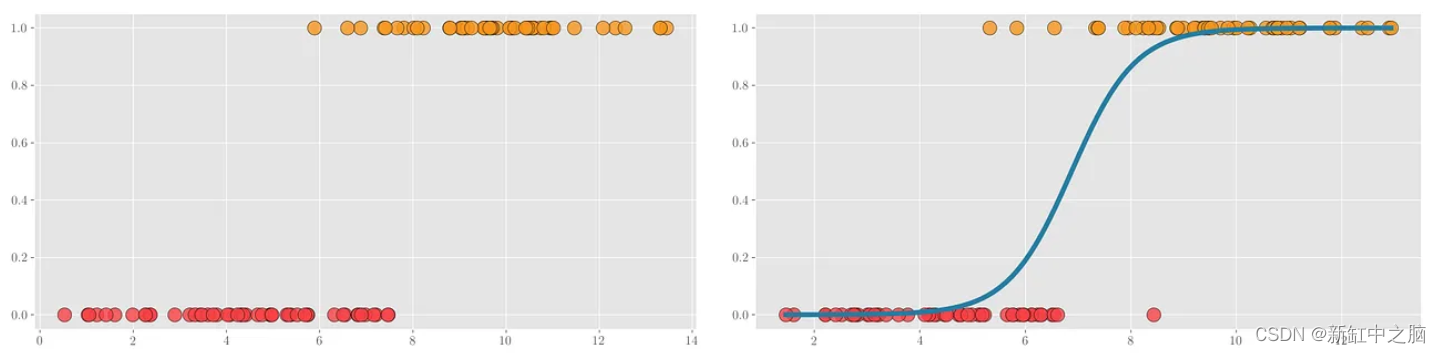
[左] 数据点散点图 - [右] 在蓝色绘制的数据点上训练的逻辑回归
逻辑回归在线性或多项式函数的输出处使用 sigmoid 函数将输出从 (-♾️, ♾️) 映射到 (0, 1)。 然后使用阈值(通常为 0.5)将测试数据分类为两个类别之一。
看起来似乎逻辑回归不是回归,而是一种分类算法。 但事实并非如此。 你可以在 Adrian 的帖子中找到更多相关信息。
10、结束语
在本文中,我们研究了回归分析中的各种方法、它们的动机是什么以及如何使用它们。 下面的表格和备忘单总结了上面讨论的不同方法。


原文链接:回归分析简明教程 — BimAnt





















 130
130











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








