1. 简介
本部分内容以一个伺服控制系统为对象,介绍了基于模型的故障诊断方法在一个实时控制系统上实现在线故障诊断的工作架构,并用奇偶空间诊断方法在EMA伺服控制系统上实现在线诊断为案例详细说明基于模型的控制系统实时故障诊断的工作原理。本文目的在于辨析物理系统的控制模型与诊断模型,并给出控制系统的模型诊断一般流程,为相关工作者提供参考。
2. 控制系统架构
给定一个控制模型一般架构,如图1所示。通过特定的控制器和传感器,该架构能实现对某一具体的物理对象的伺服控制。控制系统为一闭环架构。

图 1 控制模型一般架构
3. 基于模型的故障诊断架构
基于模型的故障诊断架构如图2所示。通过对物理对象进行建模,并认为数学模型是永远无故障的。在给物理对象和数学模型同样的控制指令的情况下,将物理对象的输出与数学模型的输出进行一定的数学变换构建诊断残差,并认为故障特征信息隐藏在残差中,从而利用评价函数和分类函数对结构化残差进行判断和分类实现基于模型的故障诊断。诊断系统为一开环架构。

图 2 基于模型的故障诊断架构
4. 基于模型的控制系统在线故障诊断架构
基于模型的控制系统在线故障诊断架构如图 3所示。黑色架构为伺服控制系统原有架构,其伺服工作不依赖于红色的诊断架构。红色为实现诊断功能时在原有控制架构上增添模块,其存在不影响伺服控制架构的正常工作。

图 3 基于模型的控制系统在线故障诊断架构
基于此架构,控制系统在实际工作时,控制器在不同工况的动态环境下始终致力于减小控制残差e, 基于模型的诊断系统在实时工作时以生成包含足够故障特征信息的高信噪比诊断残差r为首要目标。其中,r反映的是实际系统与无故障的数学模型在处理相同输入时的响应差异,而诊断系统以此为表征寻找故障特征进一步完成后续工作。
基于模型的控制系统故障诊断方法有很多种,比如系统辨识的方法、状态观测器的方法,包括常用的龙伯格观测器、未知输入观测器,H∞观测器、卡尔曼滤波器及其变种,还有奇偶方程的方法等。这里我们以奇偶空间方法为例,介绍基于模型的控制系统故障诊断的过程。
5. 案例实现:基于奇偶空间的EMA系统在线故障诊断
5.1 案例伺服系统简介
EMA为飞机上典型的伺服作动单元(图 4)。


图 4 EMA作动器
现给出某一个EMA控制系统架构如图 5所示。

图 5 EMA控制系统模型
其物理对象包含电机,减速器和舵面三部分;传感器包含位置、速度、电流三个独立测量单元;控制器包含典型的伺服系统位置速度电流三环PID控制。其中物理对象的参数如表 1。本案例中,实际的物理模型由考虑动态负载动态指令和所有测量噪声的10000Hz高精度仿真代替。
给定EMA的物理对象参数如表1所示。
表 1 物理对象参数表
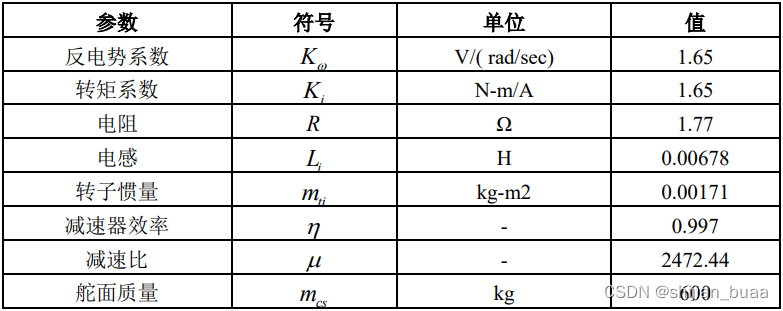
5.2 构建EMA数学模型
现针对该控制系统建立物理对象的数学模型。电机电气模型:
其中,为输入电压,
为反电势,
为电机绕组电阻,
为电机电流,以及
为电机绕组电感。电机转速为
。基于物理关系, 反电势
可表示为:
其中,是反电势系数。已知转矩系数
,可推导出电机的电磁转矩
:
电机的电磁转矩经过减速器传递到舵面,功率传递效率为以及减速比为
. 因此EMA的动力学模型可表示为:
其中 是舵面质量,
是舵面负载力的大小以及
是减速器的惯性质量。舵面的位移最终可表示为
引入状态方程来描述整个物理对象:
三个传感器的测量矩阵为:

要实现实时在线诊断,整个模型需离散化然后再计算机运行,其离散模型表示为:

其中 是诊断系统的采样和运行频率。由此,数学模型构造完毕。本案例中,诊断系统的工作频率为8Hz。
5.3 奇偶空间方法生成诊断残差
通用奇偶空间方法考虑诊断对象的物理模型如图 6所示,

图 6 诊断对象数学通用模型
其一般化表达为

其中,A、B、C、D为通用模型系统参数(EMA数学模型已推导出),x为系统多维状态(案例中为位置转速电流),u为多维输入(案例中为控制器输出电压,舵面负载力),y为舵面输出(案例中同多维状态一致)。
奇偶空间方法考虑模型和传感器可能存在着噪声和故障如图 7所示。

图 7 奇偶空间方法通用模型
其中,f为故障,v为过程噪声,n为测量噪声。L、V、M、N为故障和噪声作用到对象和传感器上的传递矩阵。此时,奇偶空间方法表示的通用模型可表示为
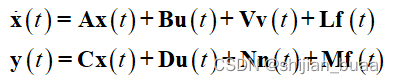
通过多阶微分(差分)可构造新的奇偶空间方程如下:

矩阵化表达后简化为
![]()
其中,

奇偶空间方程可进一步调整为
![]()
数学上可证明,能够构造若干向量w使得 ,
,因此可根据具体情况选择多个w构造矩阵
,左乘到奇偶空间方程后得到构造的多维诊断残差:
![]()
其中, 表示奇偶空间方法产生的残差只与故障
和传感器测量噪声
有关。而传感器噪声可通过进一步的信号处理方法消除,故最后得到能表征故障的有用特征。 本案例的诊断残差是数学构造产生,故没有直接的物理意义。(本部分推导较为简略,详细证明可进一步查阅奇偶空间方法相关资料)。
5.4 案例运行
EMA数学模型

奇偶空间生成三维残差的矩阵配置(此部分作者已将上述理论编入软件直接完成,如图 8):

图 8 奇偶空间生成
搭建完整的EMA故障诊断模型如图9所示。
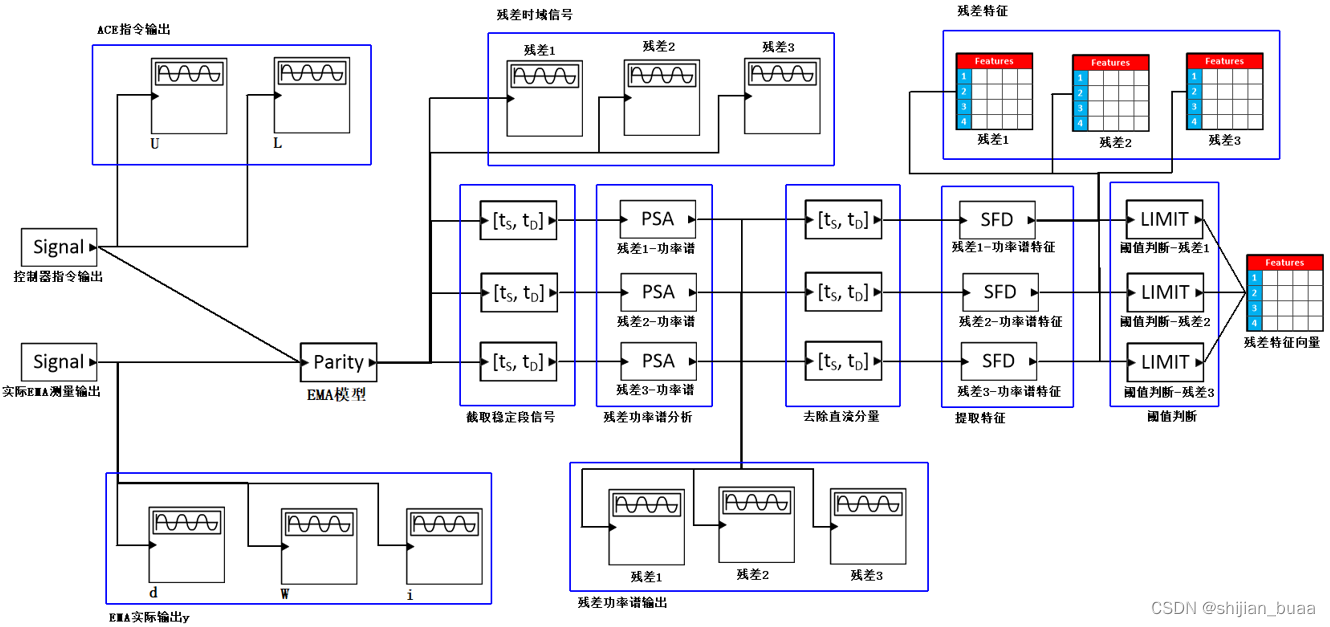
图 9 EMA故障诊断模型
EMA控制系统运行情况

图 10 EMA控制系统位置参考与位置测量信号
蓝线为飞控给出的动态舵面参考值ref,红线为传感器测出的实时舵面位置。

图 11 转速、位置和电流传感器测量值
注:该仿真工况下动态舵面参考值ref和实际负载都在实时变化,且整个过程包含噪声。
控制系统诊断的三维残差情况
残差1

图 12 正常工况诊断残差1输出

图 13 位置传感器周期性(每隔5秒)故障后残差1输出
残差2

图 14 正常工况诊断残差2输出

图 15 电机渐进退磁故障诊断残差2输出
残差3

图 16 正常工况诊断残差3输出

图 17 注入间歇性(每隔5秒)减速器故障后诊断残差3输出
残差特征提取及诊断
无故障情况
残差时域信号

残差功率谱信号

残差特征向量

位移传感器周期性故障
残差时域信号

残差功率谱信号
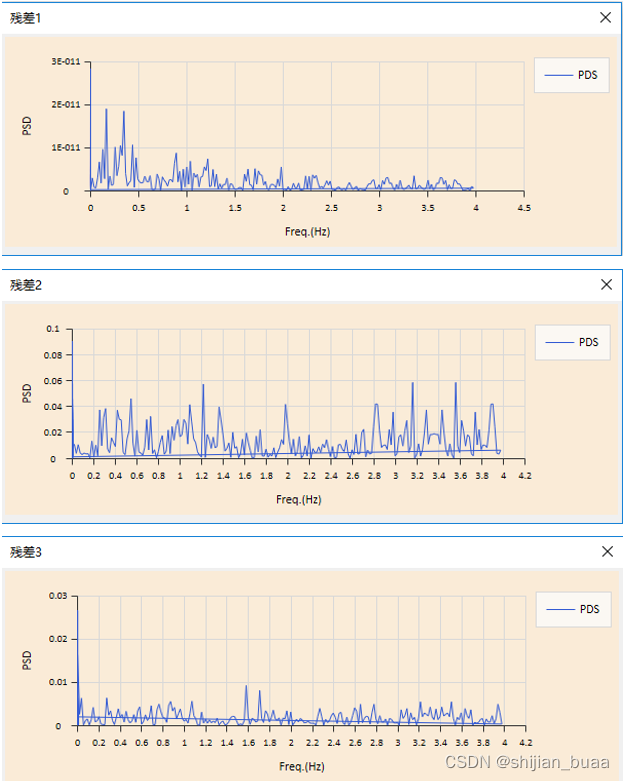
残差特征向量








 本文探讨了基于模型的故障诊断方法在实时伺服控制系统中的应用,通过奇偶空间诊断在EMA伺服系统中的实例,详细阐述了模型诊断流程,涉及控制系统架构、模型构建、在线诊断架构以及奇偶空间生成诊断残差的过程。
本文探讨了基于模型的故障诊断方法在实时伺服控制系统中的应用,通过奇偶空间诊断在EMA伺服系统中的实例,详细阐述了模型诊断流程,涉及控制系统架构、模型构建、在线诊断架构以及奇偶空间生成诊断残差的过程。
















 1654
1654

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








