通信原理-确知信号的最佳接收

写在前面：本文截屏自西安电子科技大学曹丽娜
视频学习地址：https://www.bilibili.com/video/BV1B7411o7Jo?p=34
仅供个人学习和构建知识体系所用。

确知信号：一旦某个码元波形出现时，它的所有参数都是确知的。比如：通过衡参信道到达接收机输入端的数字信号。
注意：接收机预先并不知道在每个码元时间内出现的是哪个波形。

主要内容
最佳接收机结构
误码性能和信号设计

最佳接收机结构

二进制发送码元和噪声信号的信息

接收信号为

我们的任务是：按照似然准则构造最佳接收机结构，使得误码率最小

根据似然准则

并且把似然函数代入

并且利用E0=E1

这里的W0和W1分别与发送概率P(0)和P(1)有关

构造出最佳接收机的结构

在等概率时，W0和W1相等，可以消掉，最佳接收机结构可以简化为

这里的相乘积分运算也称为相关运算，器件叫做相关器。

原理：将接收信号r(t)与可能发送的两个样本信号进行相关性比较。

注意：相关接收要求接收端提供与发送信号完全相同的信号，和相关解调需要提供本地载波一样。

能否用匹配滤波器等效相关器？
答案是对啊
在抽样时刻TB,相关器的输出：
$$y(T_B)={\int }_0^{T_B}r(u)s_i(u)du$$
i=0是上支路,i=1是下支路
匹配滤波器的输出
$$y(t)=r(t)\ast h_i(t)$$
而$$h_i(t)=s_i(T_B-t)$$
所以，此处进行了变量代换$$y(t)={\int }_{t-T_B}^{t}r(u)s_i(T_B-t+u)du$$
当t=TB时，
$$y(T_B)={\int }_0^{T_B}r(u)s_i(u)du$$i=0是上支路,i=1是下支路

可以发现相关器和匹配滤波器是等效的。等效的条件是：两者的输出在抽样时刻(t=TB)相等

误码性能和信号设计

二进制通信系统的误码率

在二进制最佳接收机的判决如下图

则错误转移概率

下面看发送码元1使，错判为0的转移概率

简写为

同理，发送码元为0，错判为1的转移概率

我们求出了误码率为

其中，积分上限分别为a和b，

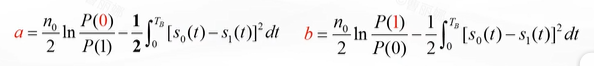
当先验概率P(0)=P(1)时，误码率可以简写

可见，当P(0)=P(1)，并给定噪声功率谱密度n0时，误码率Pe仅与两种码元波形之差的能量有关，而与波形本身无关。差别越大，c值越小，误码率越小。

下面：如何设计$s_0(t)和s_1(t)$使得误码率Pe最小？
两个码元的差异性可定量用互相关程度ρ描述

当E0=E1时，记为E0=E1=Eb，表示$s_0(t)和s_1(t)$的平均能量，此时互相关系数可以表示为

$s_0(t)和s_1(t)$的不同关系

下面建立误码率Pe和互相关系数ρ的关系

最终关系为：互补误差形式

当Eb/n0一定时，Pe时相关系数ρ的函数
由于互补误差函数是自变量的单调递减函数，所以ρ越小，自变量越大，误码率越小。所以当ρ=-1时，误码率最小。

误码率Pe通过互相关系数ρ与信号码元$s_0(t)和s_1(t)$建立关系
总结如下图

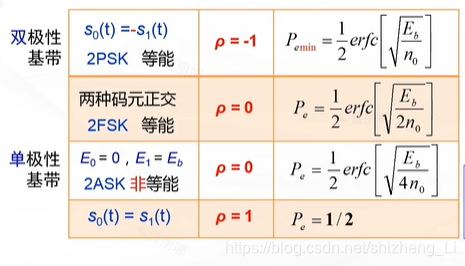
归纳

结论
$\frac{E_b}{n_0}$一定时，误码率取决于ρ（码元差异性）
ρ=-1的信号时最佳信号形式
2PSK的信号性能最佳，2FSK次之，2ASK最差