np.linalg.eigh特征值、特征向量的对应关系

import numpy as np
a=np.array([[1,2,2],[2,1,2],[2,2,1]])
w,v=np.linalg.eigh(a)
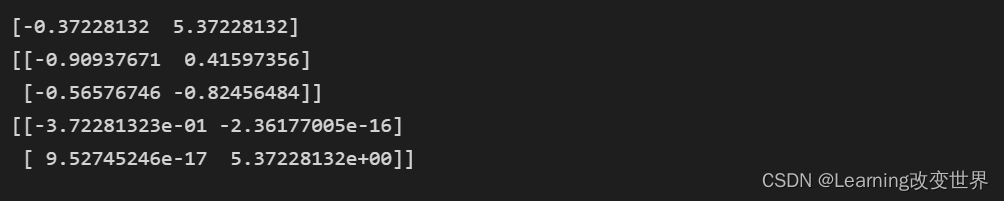
print(w)
print(v)
print(v.T.dot(a.dot(v)))

可见得到的v的每一列为一个特征向量，
$v^T\cdot a\cdot v=diag({\lambda }_1,...,{\lambda }_n)$

!!!注意只有a为对称阵结果才为对角矩阵,反例如下

import numpy as np
import numpy.linalg as LA
a=np.array([[1,3],[2,4]],dtype=float)
w,v=np.linalg.eigh(a)
print(c)
print(v.T.dot(a.dot(v)))

这是因为$A\cdot v=v\cdot diag({\lambda }_1,{\lambda }_n),v^{-1}\cdot A\cdot v=diag({\lambda }_1,...,{\lambda }_n),但对一般的矩阵v^T\ne v^{-1}$

import numpy as np
import numpy.linalg as LA
a=np.array([[1,3],[2,4]],dtype=float)
c,b=np.linalg.eig(a)
print(c)
print(b.T);   
print(LA.inv(b).dot(a.dot(b)))