第二课 监督学习应用 梯度下降

1. 最小均方误差算法

$h(x)$ 为目标函数
$\theta$ 为参数parameters
$x_{n}$为特征
$n$为特征个数
$m$为训练集的个数
则在线性假设下

$$h(x)=h_{\theta }(x)=\theta _{0}+\theta _{1}*x_{1}+\theta _{2}*x_{2}+...+\theta_{n}*x_{n}$$
即
$$h(x)=h_{\theta }(x)=\sum_{i=0}^{n}\theta _i*x_{i}=\Theta ^TX$$
根据训练集（training sets）求出 $\Theta$
其中一种方法为最小二乘方（LMS，least mean squares）：
$$min_{\theta}\ \ J(\theta)$$
其中
$$J(\theta)=\frac{1}{2}\sum_{i=1}^{n}(h_{\theta}(x^i)-y^i)^2$$
表示估计值与真实值之间的误差

计算求解$\theta$的一种方法为梯度下降法：

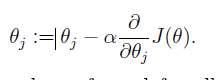
考虑只有一个样本点时


重复对上式计算，直到$\theta$值不变时，结果收敛。
其中，$\alpha$为调整收敛速度大小的参数，该算法结果与初始值的设定有关，结果可能是局部最优解（local optimal）。在线性假设下，该结果为全局最优解。

将该方法拓展到对个训练对象时，有两种梯度下降方法，第一种叫做批量梯度下降(batch gradient descent)：

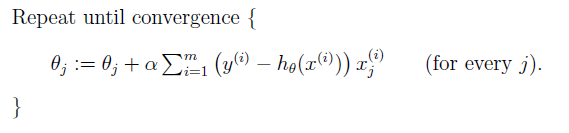
该方法最小化所有训练样本的损失函数，使得最终求解的是全局的最优解，即求解的参数是使得风险函数最小。计算量大

另外一种叫做随机梯度下降(stochastic gradient descent)：

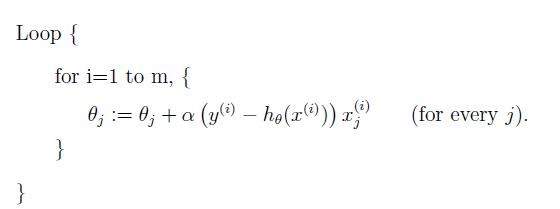
该方法最小化每条样本的损失函数，虽然不是每次迭代得到的损失函数都向着全局最优方向， 但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。计算量小

2.一些常见方程

2.1矩阵微分

矩阵微分的符号为：

迹的符号为

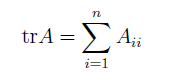
关于矩阵迹的一些性质




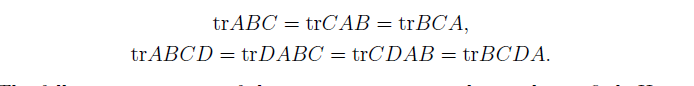
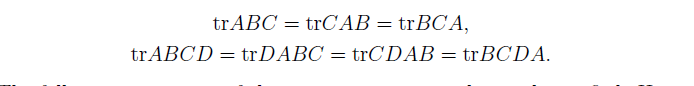
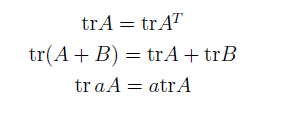
这些性质可以自己证明

2.2再探最小均方差

下面将用矩阵运算的思想来求解最小均方差的解
首先把目标函数使用矩阵形式表示



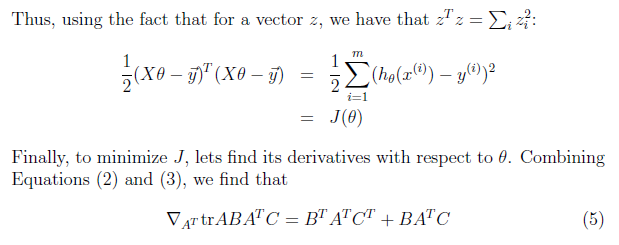
上式证明，将问题矩阵化后，导数为0，可以求出$\theta$的值