电机控制系列模块解析（第八篇）—— 高频注入法

一、基本原理

在电机控制领域，高频方波注入法常用于估计转子的位置和转速。其工作原理是每隔一定的时间间隔在电机输出电压上叠加一个电压脉冲。然后，在两相静止坐标系下或者同步旋转坐标系下对采样时刻的电压和电流进行相应的计算，以实现对转子位置和转速的估计。

方波电压注入的方式可以有两种：一种是将方波信号注入到直轴电压上（同步旋转坐标系），另一种是将方波信号注入到 α-β 轴电压上（两相静止坐标系）。这两种方式都能将方波信号注入到电机的定子电压中，并通过控制策略（如FOC）控制逆变器来最终作用于电机或其他设备。

高频方波注入法的原理还涉及到信号处理和控制理论。通过调节方波的频率、占空比等参数，可以改变电路中的高频电流或电压波形，从而实现对电路或设备的精确控制。同时，需要考虑到逆变器非线性、以及不同类型电机结构带来的非线性等因素对高频注入法的影响，需要进行相应的补偿。

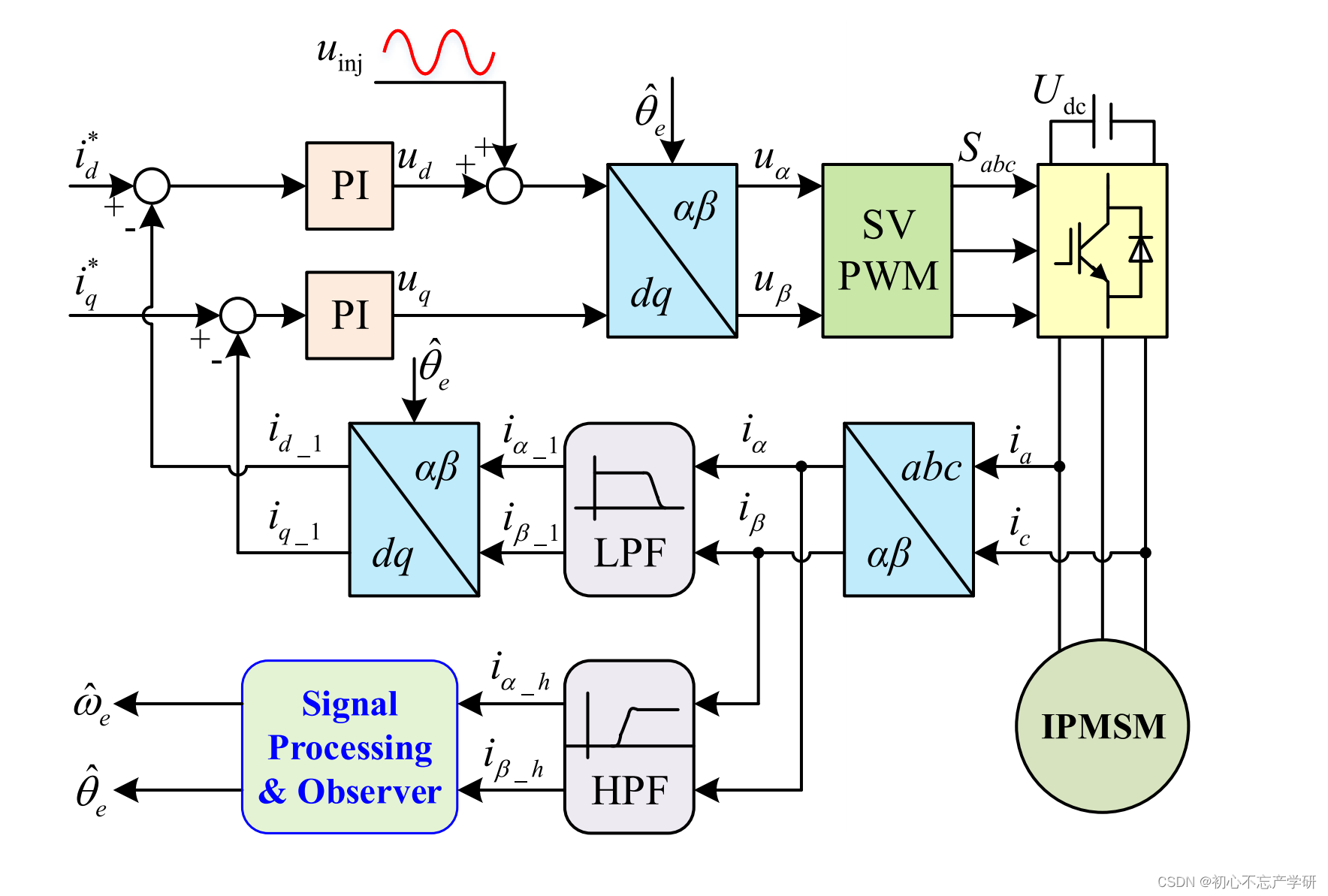
 此图片来源于网络

此图片来源于网络

脉振高频注入法，顾名思义，就是在假想的直轴电压（此处控制策略主要以基于转子磁场定向的矢量控制（FOC）为例）上叠加高频分量，该分量可以是高频方波或者弦波以及其他类型高频信号，高频注入法的原理公式表达比较简单：

此图片来源于网络

其中 Rs、 ωe 和 ψ pm 分别是定子电阻、电气角速度和永磁体磁链，Ld 和 Lq 是表观 d 轴和 q 轴电感，Ldh 和 Lqh 是增量 d 轴和 q 轴电感，Ldqh 和 Lqdh 是交叉耦合电感，它们的值相等。与描述磁链与电流之比的视在电感不同，高频电感（又称为增量电感）描述了磁链与电流之比的变化率。Ur d，ur q，ir d 和 i r q 是 dq 轴的电压和电流，“ p”表示微分算子，上标“ r”表示 SRRF（假想的同步旋转坐标系，又称为估计的同步旋转坐标系）。

针对高频电压注入永磁同步电动机的无位置传感器控制问题，通过忽略上述公式中的速度依赖项和电阻项（这个假设带来的问题以后讨论），SRRF 中高频电压方程如下：

代入要注入的高频信号，再进行坐标变换就可以得到高频电流的表达式如下：

假设交叉饱和效应带来的角度误差被补偿（在线或者离线），那就可以通过最小化交轴电流的高频分量来得到电机转子角度，具体方法可以是观测器或者锁相环以及其他方法。此处涉及的电机多为IPMSM或者SRM（同步磁阻电机），SPMSM及其他电机的高频注入法还没有正式的商用产品。

二、转矩表达式

此处参考相关文献的推导，利用增量电感求取电磁转矩：

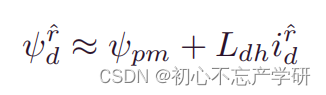
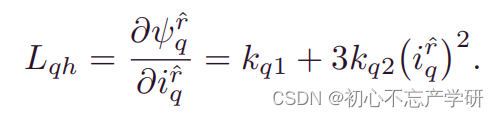
此处的三阶多项式展开是精确性和实现简单性之间的一个很好的折衷，其中第一个系数为交轴电流等于0附近时的增量电感。

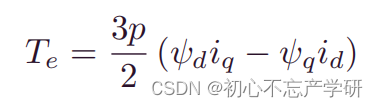
三、安全区域分析

高频注入法的安全运行区域定义为有一定信噪比的可测量的高频信号可以用来可靠地提取电机的转子位置的电机运行区域。该运行区域可以是以交直轴电流坐标系或者交直轴定子磁链坐标系来表示（后续分析高频注入可行性以及改进方法时进行详述）。另外，此处仅考虑零低速。

通过参考文献，此处分析特定工作点（某一个平衡点）的高频注入的收敛性，高频电流表达式：

ΔIε 由高频电感决定，高频电感随实际电流的变化而变化。如果电流基准的幅值是固定的，实际的基波电流随着位置估计误差的变化而变化。因此，信号 ΔIε 也随估计误差而变化，可以表示为上式所示。

为了获得可靠的收敛性，观测器输入信号 ΔIε 应该具有与位置误差 Δθr = (θr-θr)相对的正斜率过零点，这保证了闭环位置观测器的负反馈特性（此处以锁相环为例，其通过负反馈机制来实现对电机转子位置的估计）。

在电流参考下的轨迹图 （ΔIε-Δθr坐标系），条件为：i * d =-0.9 A，i * q = 3.7 A ，对高频电感进行有限元分析可得：

 此图片来源于网络

在这个电流参考下，可以得出几个关于稳定性的结果。

首先，由于轨迹在 Δθr = 0 ° 时具有正斜率，因此可以实现收敛。位置观测器过零点的斜率 Slew0表示负反馈效应的强弱程度，其与位置观测器的动态性能密切相关。

然后，Hθ 表示正斜率收敛区域的宽度是动态过程中允许的最大误差。如果位置误差由于大的干扰而超过这个极限，估计值可能会发生偏差，从而可能导致估计无法收敛。

第三，收敛区域的高度 Ha 表示可能导致不稳定的扰动的最小要求值。这个高度与注入电压的幅值成正比。而由图可知该高度越小，估计算法的收敛区域就越小。

用于评估观测器稳定性和收敛性的误差轨迹随电流参考的不同而变化，可用基于磁链MAP的方法计算，待后续进行讨论。 

四、应用场合简述

高频注入法主要针对需要精确控制电机位置和转速的应用场合。具体来说，它在以下领域中得到了广泛应用：

1. 低速和零速运行场合：在电机处于低速或零速时，传统的基于反电动势的位置估计方法往往失效。高频注入法能够在这些情况下有效工作，通过注入高频信号并观测其响应，从而准确估计电机的位置和转速。

2. 无传感器控制：在某些应用中，由于空间限制、成本考虑或维护方便性，使用物理传感器进行电机位置和转速检测可能不切实际。高频注入法作为一种无传感器技术，可以在不使用物理传感器的情况下实现精确的电机控制。

3. 凸极效应明显的电机：最初，高频注入法主要适用于凸极效应较为明显的内嵌式永磁同步电机。然而，随着技术的不断发展，高频注入法也逐渐扩展到部分表贴式永磁同步电机的应用中。

4. 对控制精度要求高的场合：如电动汽车、风力发电、工业自动化设备、航空航天等领域，这些场合对电机的控制精度和稳定性有较高要求，高频注入法能够提供精确的位置和转速估计，从而满足这些要求。

总的来说，高频注入法适用于那些需要精确控制电机位置和转速，且可能面临低速、无传感器或特定电机类型挑战的应用场合。

五、方法缺点总结

高频注入法在电机控制领域的应用虽然具有诸多优点，除了高频噪声外，也存在一些明显的缺点：

1. 电流控制器带宽要求高（仅针对高频电流注入法而言）：高频注入法需要电流控制器的带宽很大，这增加了系统的复杂性和成本。较宽的带宽要求可能限制了电流控制器的设计灵活性，同时也可能对系统的稳定性产生不利影响。

2. 磁场角度检测受负载工况影响（指电机电感的非线性影响）：高频注入法检测的磁场角度可能受到负载工况的影响，这导致检测到的角度并非完全准确的转子磁链位置角。为了补偿这种误差，需要依赖电机的参数（如查表），这在一定程度上削弱了高频注入法的鲁棒性。

3. 降低逆变器电压利用率：为了产生高频信号响应，需要施加足够大幅值的电压或电流激励。这可能导致逆变器的电压利用率降低，进而影响到整个电机驱动系统的效率。

4. 产生额外电磁转矩：注入的高频信号会在电机中产生额外的电磁转矩，这可能对电机的正常运行产生干扰，甚至导致电机性能下降。

5. 信号处理复杂：高频信号与其他高频谐波信号可能会混在一起，需要采用复杂的信号处理方法和滤波器来有效地采样高频信号。滤波器的使用可能带来电流相移和幅值畸变等问题，增加了系统设计的难度和成本。

6. 影响电流控制器的动态性能：电流信号的滤波会对电流控制器的动态性能产生影响，这在一定程度上限制了高频注入法在需要快速响应的应用场景中的使用。

虽然高频方波注入法的动态性能较好，但是方法本身还是存在上述若干个缺点，在产品中可以采用一些工程手段（标定、查表、补偿、以及随机注入等）来减小这些缺点对产品性能规格指标的影响（比如提高参数鲁棒性、减小估计误差、扩展安全运行区域、削弱高频噪声等等）。目前还有一些厂商是通过同时改进电机本体的设计、主电路的设计以及估计算法来增强高频注入法的性能。

六 、附录

以某个中低速电机为例（IPMSM），电机参数表：

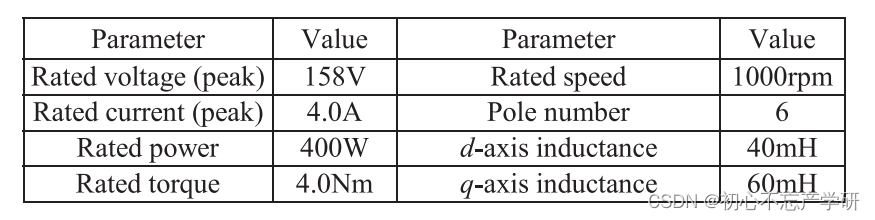
 增量电感可为磁链MAP的局部导数: