回归和分类损失函数（MSE、MAE、Huber、Exponential、Deviance、Hinge）

机器学习任务通过最小化 “目标函数” 求解，这种目标函数也称为损失函数，损失函数用于衡量模型预测期望输出的能力，损失越小，模型的预测能力越强。

损失函数大致可分为两类：分类损失和回归损失。

Regression loss

常见的回归损失：

Mean Square Error, Quadratic loss, L2 Loss

Mean Square Error (MSE) 是回归任务中最通用的损失函数，MSE是目标值与预测值之间差值平方和的均值：
$${\ell }_{\text{mse}}(f)=\frac{1}{m}[Y-f(X){]}^2$$
MSE在均值处取极小值：
$$c=\arg \underset{c}{\min }\sum _i\frac{1}{m}(y_i-c{)}^2=\text{mean}(y)$$

Mean Absolute Error, L1 Loss

Mean Absolute Error (MAE) 是目标值与预测值绝对差之和的均值，MAE不考虑误差方向，。
$${\ell }_{\text{abs}}=|y-f(\mathbf{x})|$$
MAE在中位数处取极小值：
$$c=\arg \underset{c}{\min }\sum _{y\ge c}(y-c)+\sum _{y<c}(c-y)=\text{median}(y)$$
考虑方向的损失叫做 Mean Bias Error (MBE)，是所有目标值与预测值残差之和的均值，显然小于MAE。

MSE and MAE

简而言之，使用MSE更容易拟合数据，但使用MAE模型对异常值的鲁棒性更强，让我们看看为什么？

MSE损失在错分样本的损失随目标函数值以平方级变化，而MAE损失以线性级变化，对异常值敏感度低。另一个角度是，MSE最优解位于均值处，MAE最优解位于中位数处，显然中位数解比均值解对异常值的鲁棒性更强。

MSE和MAE的选择

如果异常值对业务很重要，应该使用MSE尽可能的拟合异常值，如果异常值只是噪声数据，则应该用MAE损失。

MSE和MAE均无法拟合的情况

考虑这种情景的数据：90%数据的目标值是150，10%数据的目标值位于0-30之间。MAE可能会把全部目标值预测为150（倾向于中位数），MSE可能预测较多的值位于0-30之间（倾向于异常值），这两种情况我们都不希望看到。

那如何解决这种问题呢？一种简单的方法是转换目标变量（？？？），另一种方法是使用其它损失函数，如Huber Loss。

Huber Loss, Smooth Mean Absolute Error

Huber损失对异常值没有MSE损失敏感，通过超参数$\delta$控制多小的误差使用平方损失、多大的误差使用绝对损失，即真值附近$\delta$区间使用MAE损失，否则使用MSE损失：
$${\ell }_{\text{hub}}=\{\begin{array}{ll}|y-f(\mathbf{x}){|}^2,& |y-f(\mathbf{x})|\le \delta \\ 2\delta |y-f(\mathbf{x})|-{\delta }^2,& \text{otherwise}\end{array}$$

为什么使用Huber损失？

MAE损失在极值点附近梯度非常大，在极值点处非常不稳定，但对异常点不敏感；MSE对异常点敏感，但在接近极值点时梯度逐渐减小至0，可以得到精确极值。

Huber Loss对于包含异常点的数据集一般表现由于以上两者，异常值以MAE方式处理，极值点以MSE方式处理。

Log-Cosh Loss and Quantile Loss

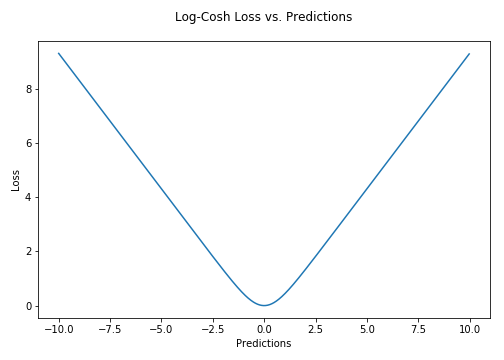Classification loss

常见的分类损失：

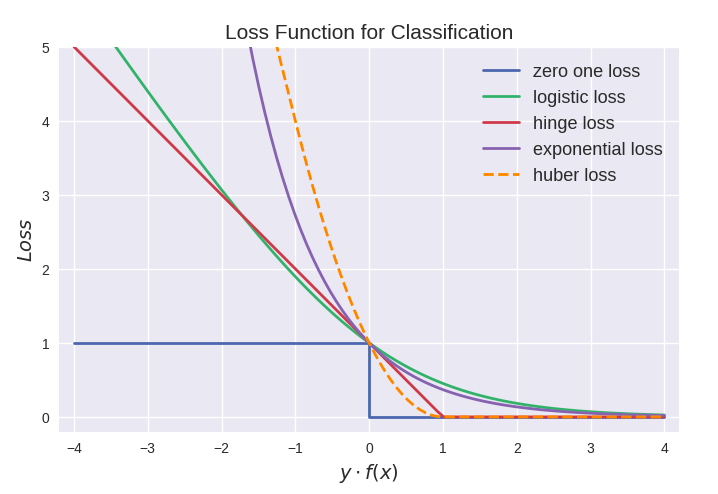
Binomial Deviance (Logistic)

令$p(x)$表示样本$\mathbf{x}$的类1概率，logistic的对数似然损失为
$$L(y^{\prime },p)=-[y^{\prime }\ln p(\mathbf{x})+(1-y^{\prime })\ln (1-p(\mathbf{x}))],p(\mathbf{x})=\frac{1}{1+\exp (-f(\mathbf{x}))}$$
则损失函数的负梯度为（sklearn-binomial deviance）
$$L(y^{\prime },f)=-y^{\prime }f(\mathbf{x})+\ln (1+\exp (f(\mathbf{x}))),-{\nabla }_{f}L=y^{\prime }-\frac{1}{1+\exp (-f(\mathbf{x}))}$$
（GBDT二分类使用Deviance损失，参数初值）模型初始值满足$c=\arg {\min }_c{\sum }_i{w}_{i}L(y_i,c)$，得
$$\sum _i{w}_i(y_i-\frac{1}{1+e^{-c}})=0⟹c=\ln \frac{{\sum }_i{w}_i{y}_i}{{\sum }_i{w}_i(1-y_i)}$$

Multinomial Deviance (Softmax)

softmax的对数似然损失
$$L(y,f_1,\cdots ,f_K)=-\sum _{k=1}^K{y}_k\ln p_k(\mathbf{x}),p_k(\mathbf{x})=\frac{\exp f_k(\mathbf{x})}{{\sum }_i\exp f_i(\mathbf{x})}$$

$y_k$表示样本$\mathbf{x}$的真实类k概率. 可令上式一个冗余目标函数为0，如$f_K(\mathbf{x})=0$.

第k个目标函数的负梯度
$$g_k=-\frac{\partial L(y,f_1,\cdots ,f_K)}{\partial f_k}=y_k-\frac{\exp f_k(\mathbf{x})}{{\sum }_i\exp f_i(\mathbf{x})}$$

Exponential Loss and Binomial Deviance Loss

给定样本$\mathbf{x}$，类别 y ∈ { − 1 , + 1 } y\in\{-1,+1\} y∈{−1,+1}，类别另一种表示 y ′ = ( y + 1 ) / 2 ∈ { 0 , 1 } y'=(y+1)/2\in\{0,1\} y′=(y+1)/2∈{0,1}.

二项偏差（Binomial Deviance）的类1概率为
$$p(\mathbf{x})=P(y=1|\mathbf{x})=\frac{\exp (f(\mathbf{x}))}{\exp (-f(\mathbf{x}))+\exp (f(\mathbf{x}))}=\frac{1}{1+\exp (-2f(\mathbf{x}))}$$
二项偏差的对数似然损失（极大化似然概率等于极小化交叉熵）
$$-[y^{\prime }\ln p(\mathbf{x})+(1-y^{\prime })\ln (1-p(\mathbf{x}))]=-\ln (1+\exp (-2yf(\mathbf{x})))$$
基于经验风险最小化求解模型，则指数损失和二项偏差损失的解具有一致性，以下公式给出
$$\begin{array}{rl}f(\mathbf{x})& =\arg \underset{f}{\min }{\mathbb{E}}_{y|\mathbf{x}}[\exp (-yf(\mathbf{x}))]\\ & =\arg \underset{f}{\min }P(y=1|\mathbf{x})\cdot \exp (-f(\mathbf{x}))+P(y=-1|\mathbf{x})\cdot \exp (f(\mathbf{x}))\\ & =\frac{1}{2}\ln \frac{P(y=1|x)}{P(y=-1|x)}\\ & =\arg \underset{f}{\min }{\mathbb{E}}_{y|\mathbf{x}}[-\ln (1+\exp (-2yf(\mathbf{x})))]\end{array}$$

但两者在错分样本上损失程度不同，指数损失在错分样本的损失随目标函数取值以指数级变化（对异常值敏感如类标错误数据），而二项偏差损失以线性级变化.

Hinge Loss (SVM)

合页损失是SVM的损失函数，对于$yf(x)>1$的点，合页损失都是0，由此带来了稀疏解，使得SVM仅通过少量的支持向量就能确定最终分类超平面。

SVM的损失函数是合页损失 + L2正则化。

Reference

1. Regression Loss Functions All Machine Learners Should Know
2. 常见回归和分类损失函数比较