离散特征之间的相关性

  在数据挖掘的时候，有时候我们会想计算不同特征之间的相关，比如在建模时用来减少冗余特征。连续特征之间的相关性很简单，用皮尔逊相关就可以了，是非常通用且有效的方法。但是在实践里面，大部分时候我们处理的是离散特征，所以这里想提出一个离散特征之间的相关计算办法。这是之前在看决策树C4.5的时候想到的一个思路，就是离散特征之间的相关，可以用决策树的经典算法中的信息增益和信息增益比来描述。

  假定有一组数据集S，两个离散特征分别为A和B。Entropy(SA)表示使用特征A对数据集S进行分类后，所对应的信息熵（如果是在分类问题里，那么这个特征A就是希望学会的分类）。信息熵的形式为

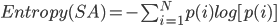
p(i)是特征A中，样品属于第i类的概率。如果样品都属于一个类别，那么Entropy(SA)=0，相反，样品类别越多，分布越均匀，则信息熵越大，也可以说这组数据的不纯度越高。比如A代表是否会打篮球这个特征，如果样品都是会打的，那么纯度就很高。

  决策树算法中的信息增益，被定义为

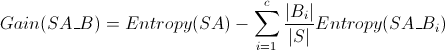
这个式子看起来有点复杂，其中Gain(SA_B)表示加入特征B分类之后的信息增益，i是根据特征B来分类的第i个类别，Bi是第i个类别的样品集合&#x