前言
最近论文快deadline了,一直没空更新…今天复习一下多尺度特征融合的常用操作。
1. FPN 特征金字塔
论文:feature pyramid networks for object detection 论文链接
设计思路:
- 底层的特征语义信息比较少,但是目标位置准确。
- 高层的特征
语义信息比较丰富,但是目标位置比较粗略。
模型设计:自底向上Bottom-up,自顶向下Top-down,横向连接Lateral connection。

- 自底向上:特征图随着左半部分的网络的加深,尺寸会不断变小,语义信息会更加丰富,这里是将每个stage(尺寸不变的网络集合为一个stage)的最后一个特征图构成特征金字塔。
- 自顶向下:通过upsampling的方法,不断放大特征图,使得低层特征也包含丰富的语义信息。
- 横向连接:将上采样的结果和自底向上生成的相同大小的特征图进行融合。即:从左边过来的特征图,先经过1*1的卷积操作,然后与上面下来的特征图相加(element-wise addition),之后再经过3*3的卷积能得到本层的特征输出(消除上采样产生的混叠效应aliasing effect:插值生成的图像灰度不连续,在灰度变化的地方可能出现明显的锯齿状)。
FPN+RPN
原先的RPN网络,输入的是经过主干网络提取的特征图(单尺度),设置的anchor有3种尺寸,3种宽高比,故有9种anchor:
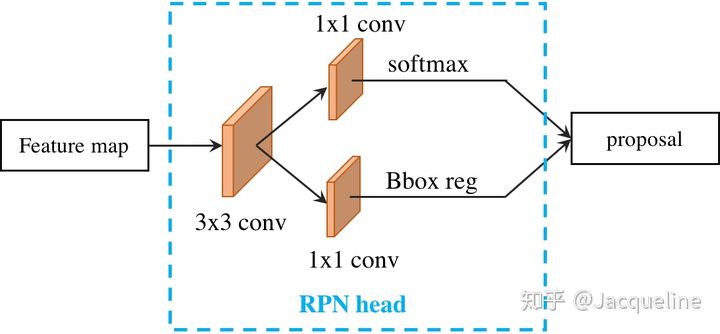
加入了FPN后,RPN的输入是多尺度特征图,也就是每一层特征图后连接一个RPN head,因为已经有多尺度特征图了,就不需要设置另外3种尺寸,故有15种anchor:

FPN+ROI
ROI的作用是将输入的(检测框,整特征图)进行pooling,得到相同尺寸的目标特征图。使用了FPN之后,就有了多尺度特征图,考虑到实际目标有大有小,所以使用下公式判断将哪一层的特征图输入到ROI中:
k
=
⌊
k
0
+
l
o
g
2
(
w
∗
h
224
)
⌋
k=\lfloor{k_0+log_2(\frac{\sqrt{w*h}}{224})}\rfloor
k=⌊k0+log2(224w∗h)⌋
其中,
k
k
k代表特征图的层数编号。
2. PANet
Pyramid Attention Networks for Image Restoration
论文地址
PANet是FPN(图a)的拓展,PANet创新点在于:
- 加入了自底向上路线增强;
- 加入了自适应特征池化。

-
Bottom-up Path Augmentation
可以看到图(a)的FPN是自顶向下路线,通过侧向连接,将高层的强语义特征传递下来,只增强了特征金字塔的语义信息。例如,当底层特征到到P5时(红线),中间经过非常多层的网络(100+),此时底层的目标信息已经非常模糊了,因此扩展了FPN,加入了自底向上的路线(绿色路线,底层->P2->N2~N5,其中经过的路径少于10层),弥补并加强了定位信息。 -
Adaptive Feature Pooling
前文中,使用FPN+ROI的方法是使用公式来选择FPN的特征图(P2~P5)的其中之一(例如小尺寸选择P2,大尺寸选择了P5)作为ROI的输入,而这种方法实际上也是单层的特征图。在这里,作者对多个特征图(N2~N5)和目标框进行ROI,然后对多个ROI结果(4个),分别经过全连接(fc1)后,再进行融合(sum、max、product等),如图所示:

参考
https://zhuanlan.zhihu.com/p/62604038



























 700
700

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










