数理统计笔记6：假设检验

最新推荐文章于 2024-06-11 10:59:59 发布

小林up

最新推荐文章于 2024-06-11 10:59:59 发布

阅读量1.3k

点赞数 3

分类专栏： # 概率论文章标签：假设检验置信区间 p值数理统计

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/subtitle_/article/details/128011934

版权

概率论专栏收录该内容

12 篇文章

订阅专栏

引言

数理统计笔记的第6篇先介绍了假设检验，给出了各种常用的假设检验的方法，最后介绍了用置信区间和p值来进行假设检验的方法。

假设检验描述

什么是假设

在这里插入图片描述

什么是假设检验

在这里插入图片描述

假设检验的基本思想

在这里插入图片描述

假设检验的步骤

在这里插入图片描述

注意：要接受的结论放在备择假设，要拒绝的结论放在原假设，我们的目的是要看能不能拒绝原假设。
在这里插入图片描述

在这里插入图片描述

当计算的统计量出现在拒绝域上时，这种情况出现的概率本应该特别小，基本不可能出现，但还是出现了，所以我们就有很大的可能性去猜测原假设是错误的，但是我们最后的结论是原假设以一定概率( $1-\alpha$ )不被接受，而不是直接接受备择假设。这是一种否定对立面的方式，但是也不代表着肯定（这个地方有点绕）。

举个栗子，比如我要验证你一天玩手机的时间T小于6小时，原假设是T>=6，备择假设就是T<6（拒绝域）。检验出来计算结果在拒绝域内（置信度比如说是5%），我们结论就是有95%的概率认为你一天玩手机的时间T不小于6小时。

假设检验的原理

在这里插入图片描述

假设检验的两类错误

在这里插入图片描述

双侧检验和单侧检验

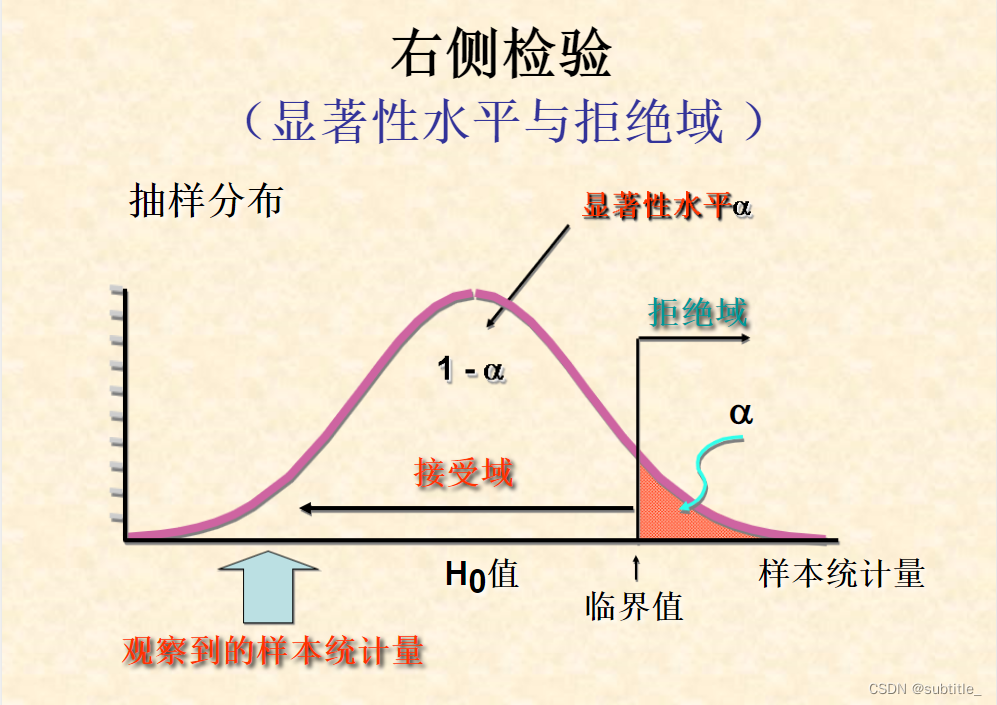
在这里插入图片描述

单个正态总体的参数检验

在这里插入图片描述

总体方差已知的均值检验-双尾Z检验

在这里插入图片描述

例子

在这里插入图片描述

在这里插入图片描述

总体方差已知的均值检验-单尾Z检验

在这里插入图片描述

在这里插入图片描述

例子

在这里插入图片描述

在这里插入图片描述

总体方差未知的均值检验-双尾t检验

在这里插入图片描述

例子

在这里插入图片描述

在这里插入图片描述

总体方差未知的均值检验-单尾t检验

统计量和双尾t检验一样，原假设和备择假设换一下，参考前面的总体方差已知的均值检验-单尾Z检验的假设。

例子

在这里插入图片描述

总体比例的假设检验-Z检验

在这里插入图片描述

例子

在这里插入图片描述

单个总体方差的检验- $\chi^2$ 检验

在这里插入图片描述

例子

在这里插入图片描述

两个正态总体的参数检验

在这里插入图片描述

在这里插入图片描述

总体方差已知的两个总体均值之差的检验-Z检验

在这里插入图片描述

在这里插入图片描述

例子

在这里插入图片描述

总体方差未知但相等的两个总体均值之差的检验-t检验

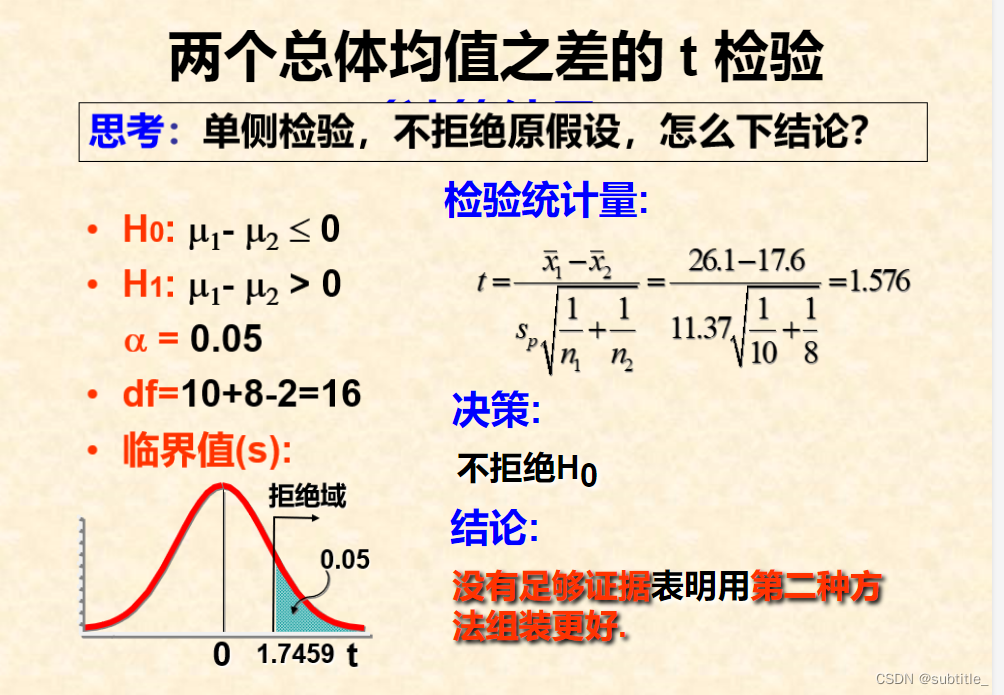
在这里插入图片描述

例子

在这里插入图片描述

假设检验中的其他问题

在这里插入图片描述

使用置信区间进行假设检验

在这里插入图片描述

例子

在这里插入图片描述

使用p值进行假设检验

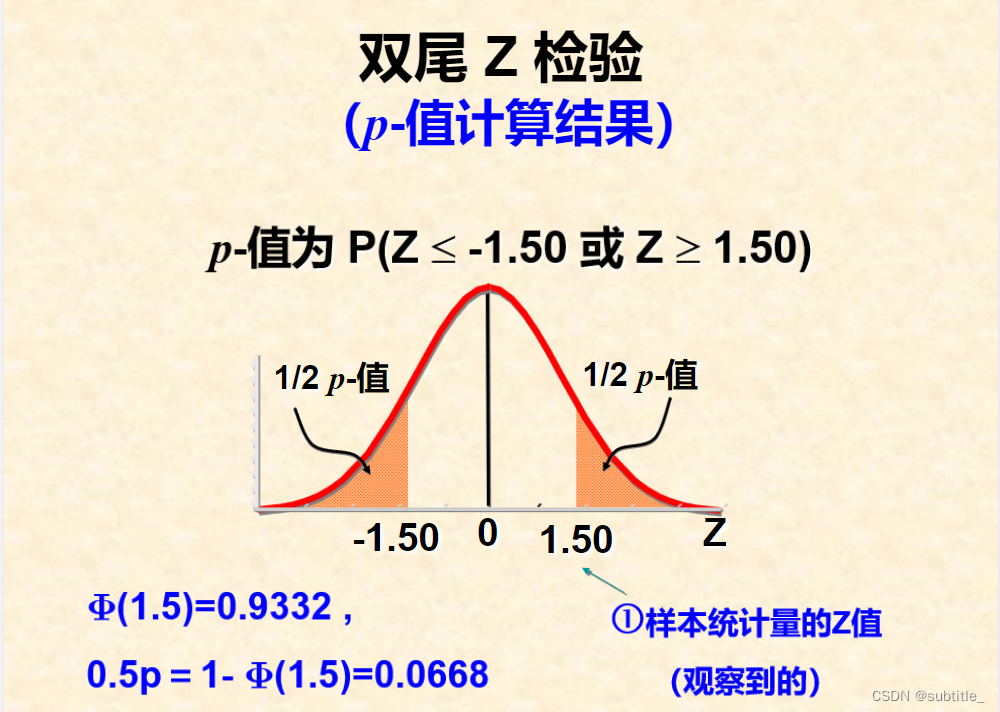
在这里插入图片描述

例子1

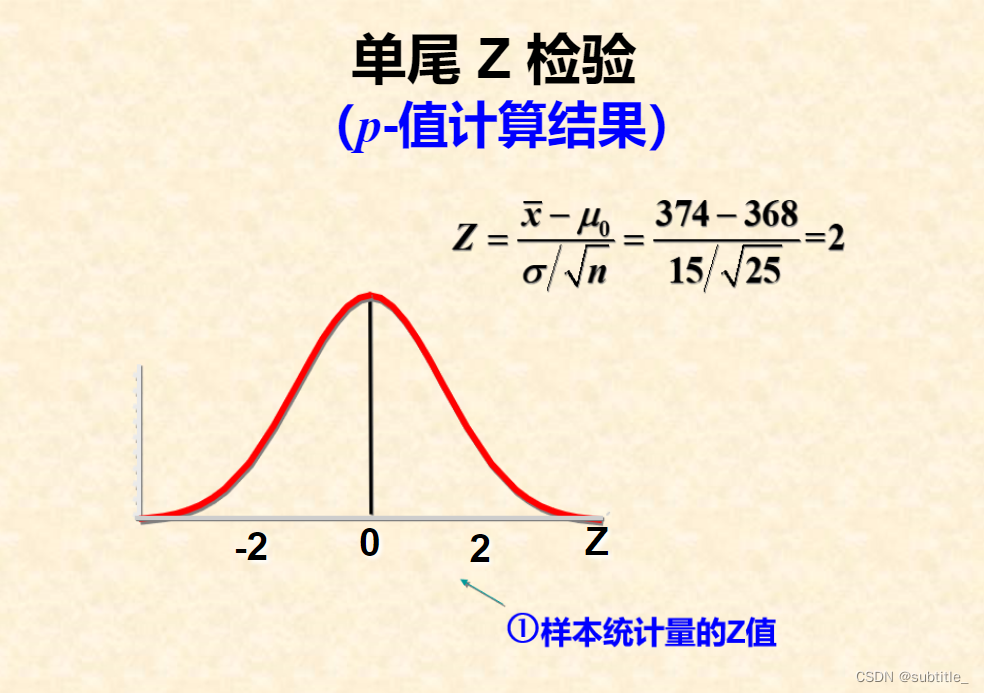
在这里插入图片描述

在这里插入图片描述

例子2

在这里插入图片描述

在这里插入图片描述

使用p值法的注意事项

在这里插入图片描述

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。