[透彻理解]由最小二乘到SVD分解

[透彻理解]由最小二乘到SVD分解

借鉴的材料：

https://www.cnblogs.com/hxjbc/p/7443630.html

https://blog.csdn.net/macer3/article/details/48394239/

https://zhuanlan.zhihu.com/p/57803955

前言：最近在整理项目资料，其中有一个三维点云地面部分的提取。关于其理论，在此做一个整理。

1 问题引入：二维直线的拟合问题

假设我们有：$A:(1,2),B:(0,2),C:(2,3)$三个点，现在需要对这个三个点拟合一条直线。

设这条直线的方程为$y=ax+b$ 。我们希望这条直线可以同时通过这三个点，也就是这条直线的参数要满足:
$$\{\begin{array}{l}1\times k+b=2\\ 0\times k+b=2\\ 2\times k+b=3\end{array}$$
这是一个超定方程。为了后面表示方便，在这里我们用$x_1,x_2$来代替$k,b$。
$$\{\begin{array}{l}1\times x_1+x_2=2\\ 0\times x_1+x_2=2\\ 2\times x_1+x_2=3\end{array}$$
写成矩阵的形式：
$$\begin{array}{l}\left[\begin{array}{l}11\\ 01\\ 21\end{array}\right]\left[\begin{array}{l}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{l}2\\ 2\\ 3\end{array}\right]\\ \uparrow \uparrow \uparrow \\ A\times x=b\end{array}$$
这即是我们要优化的非齐次线性方程组$Ax=b$。

为了方便我们接下来的理解，现在将其拆分成下面这种形式：
$$\begin{array}{l}\left[\begin{array}{l}1\\ 0\\ 2\end{array}\right]\times x_1+\left[\begin{array}{l}1\\ 1\\ 1\end{array}\right]\times x_2=\left[\begin{array}{l}2\\ 2\\ 3\end{array}\right]\\ \uparrow \uparrow \uparrow \\ a_1\times x_1+a_2\times x_2=b\end{array}$$
这里的理解方式是，两个3维向量，经过$x_1$和$x_2$的线性组合之后，得到$b$向量。

这里更高级一点的说法是，在以$a_1,a_2$为基向量(3维)所张成的2维子空间上，寻找最接近$b$向量的向量。

把$a_1,a_2$视作基向量，画图理解。

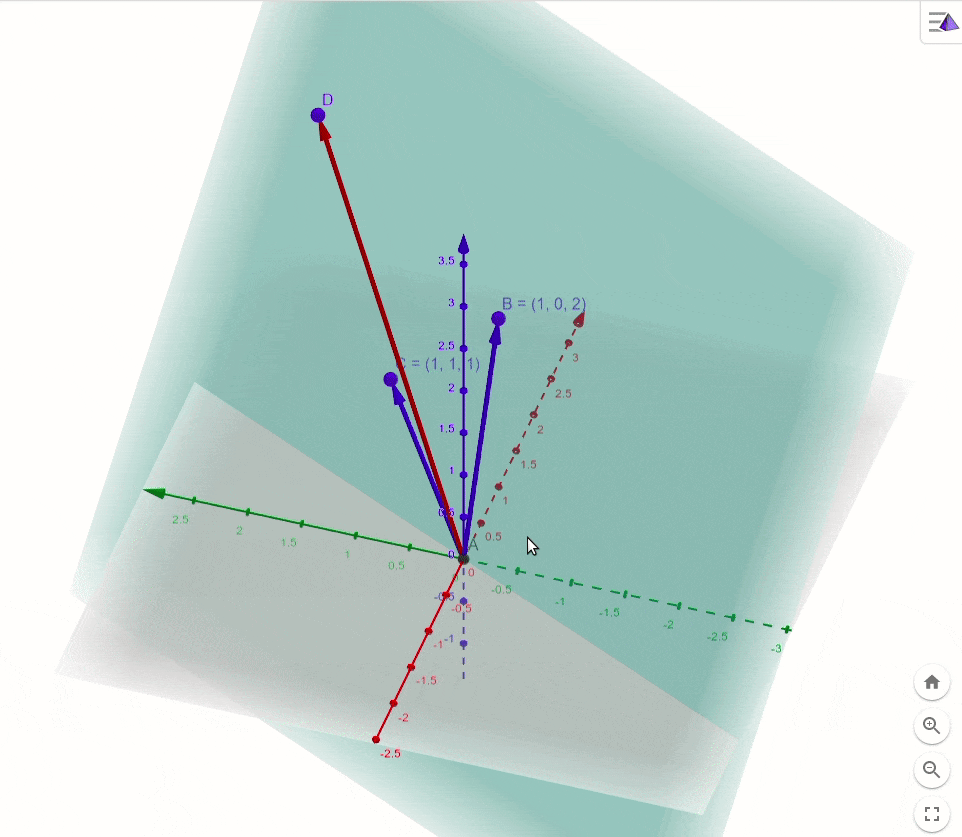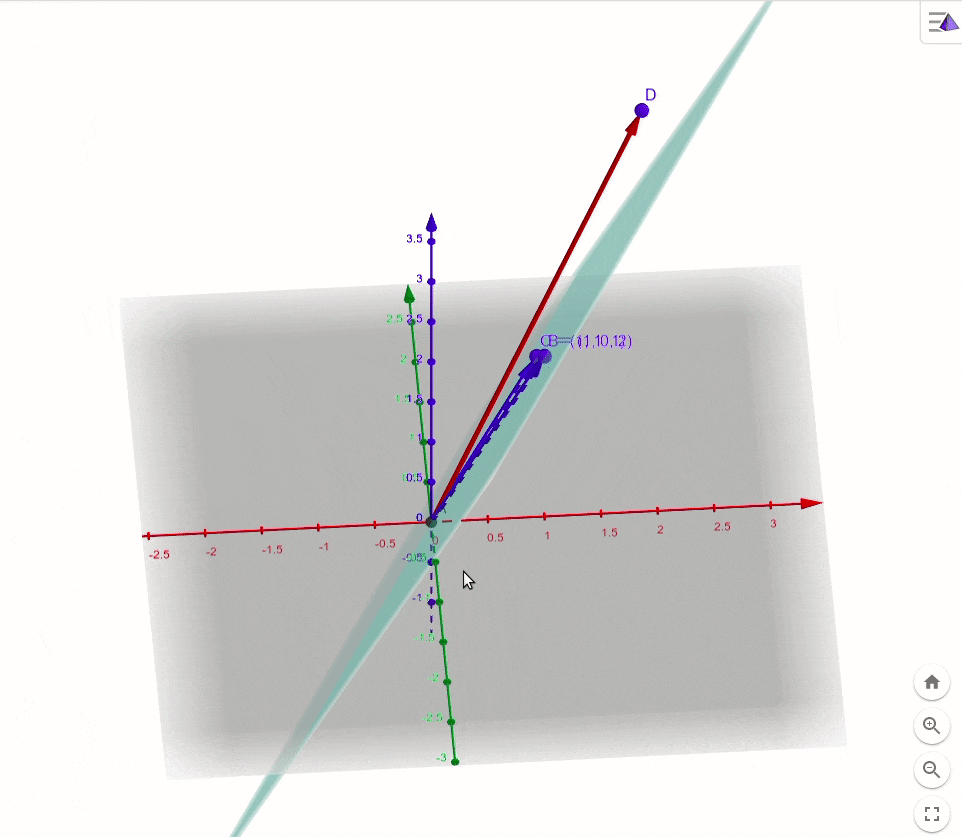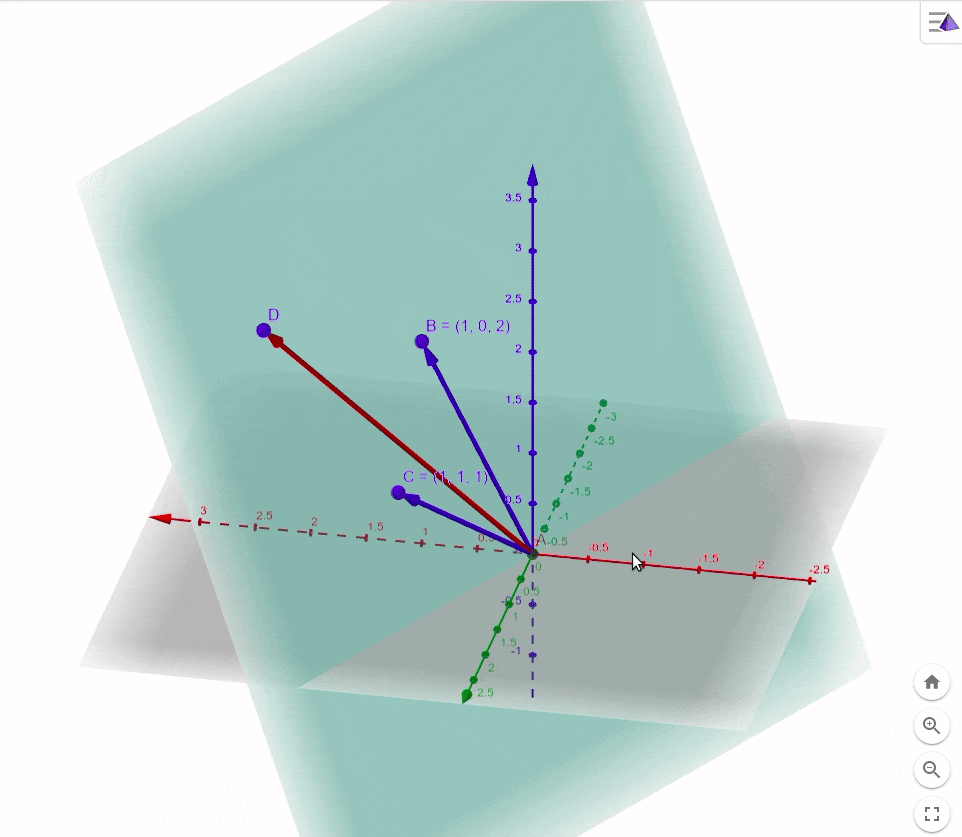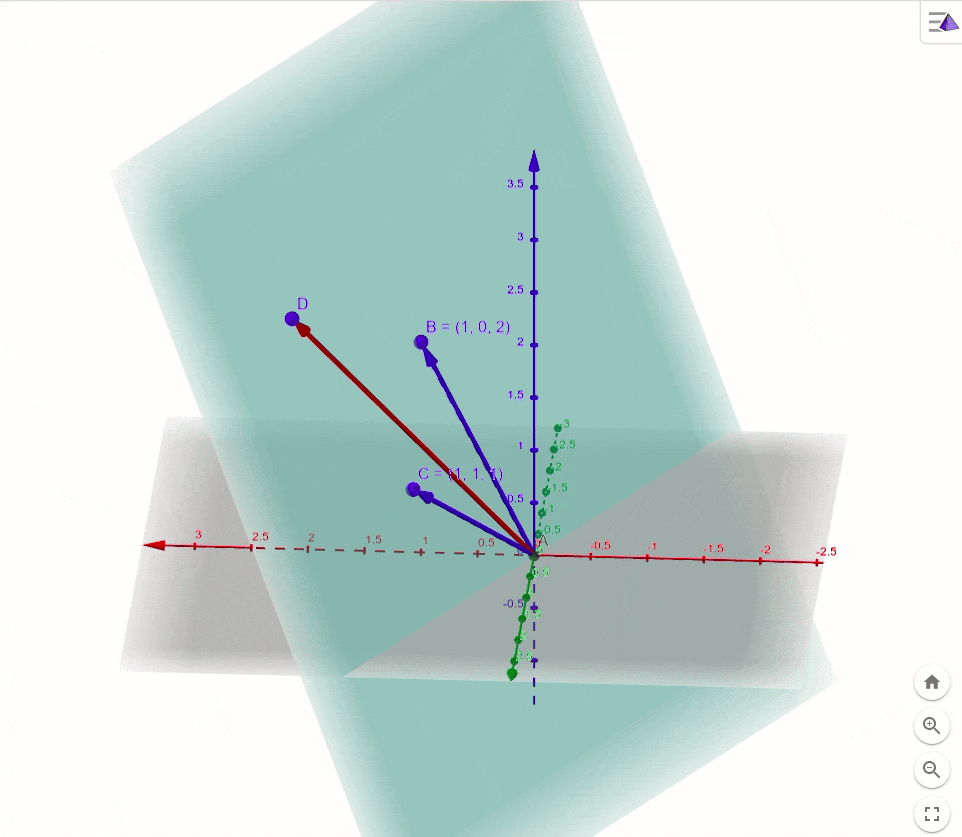
由这个图可知，公式(4)肯定是不成立的，因为向量$b$(红色)就不在基向量$a_1,a_2$所张成的二维平面（二维子空间）里。

所以，我们在这里退而求其次，在该二维子空间中找一个向量$b^{\prime }$（由基向量组成$b^{\prime }=x_1\ast a_1+x_2\ast a_2$），来代替向量$b$，但是这个向量距离$b^{\prime }$到向量$b$的距离最短（如下图所示）

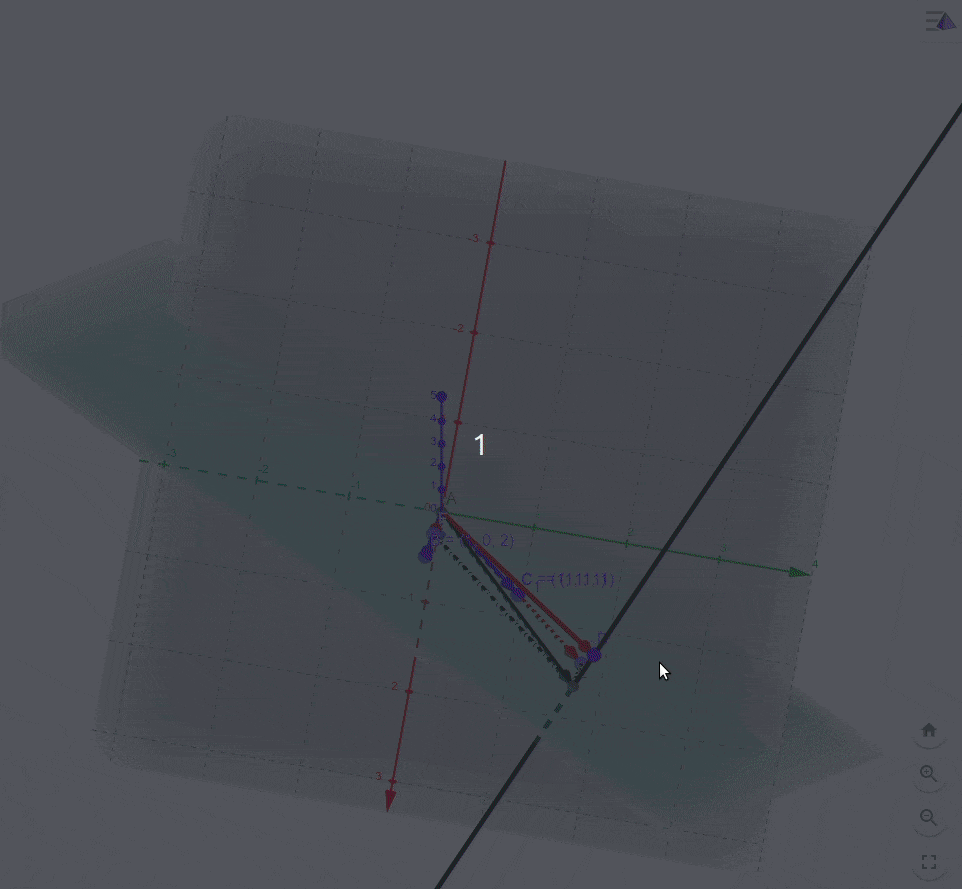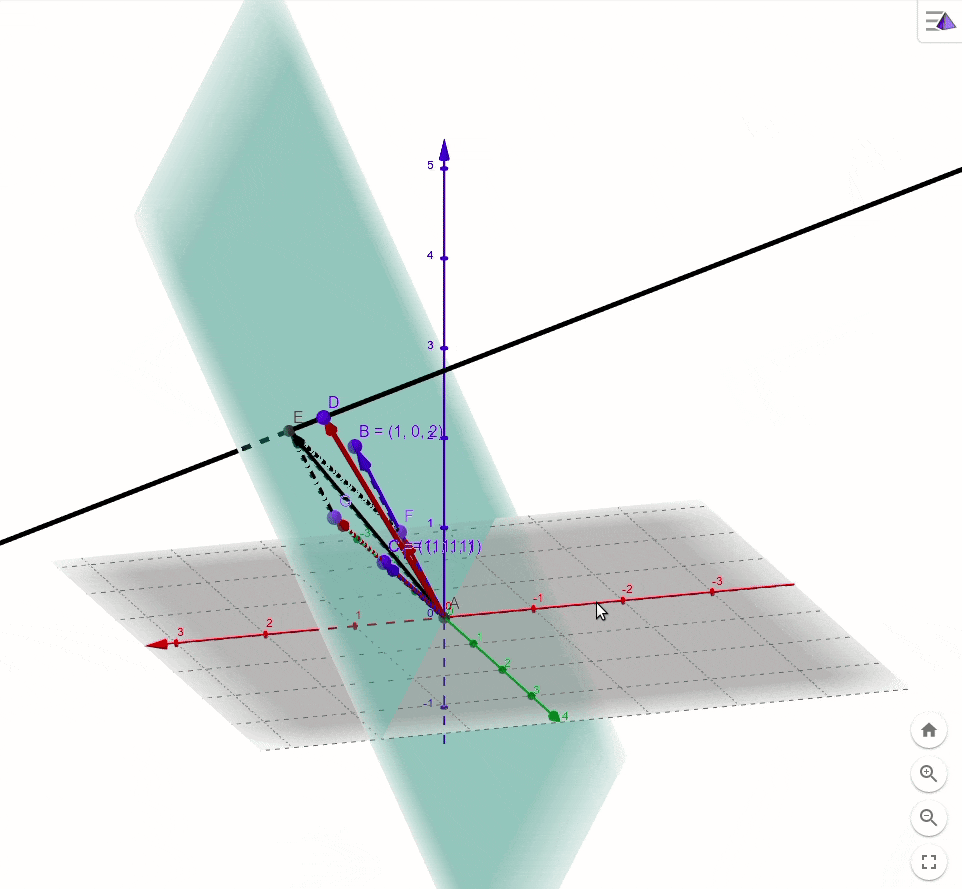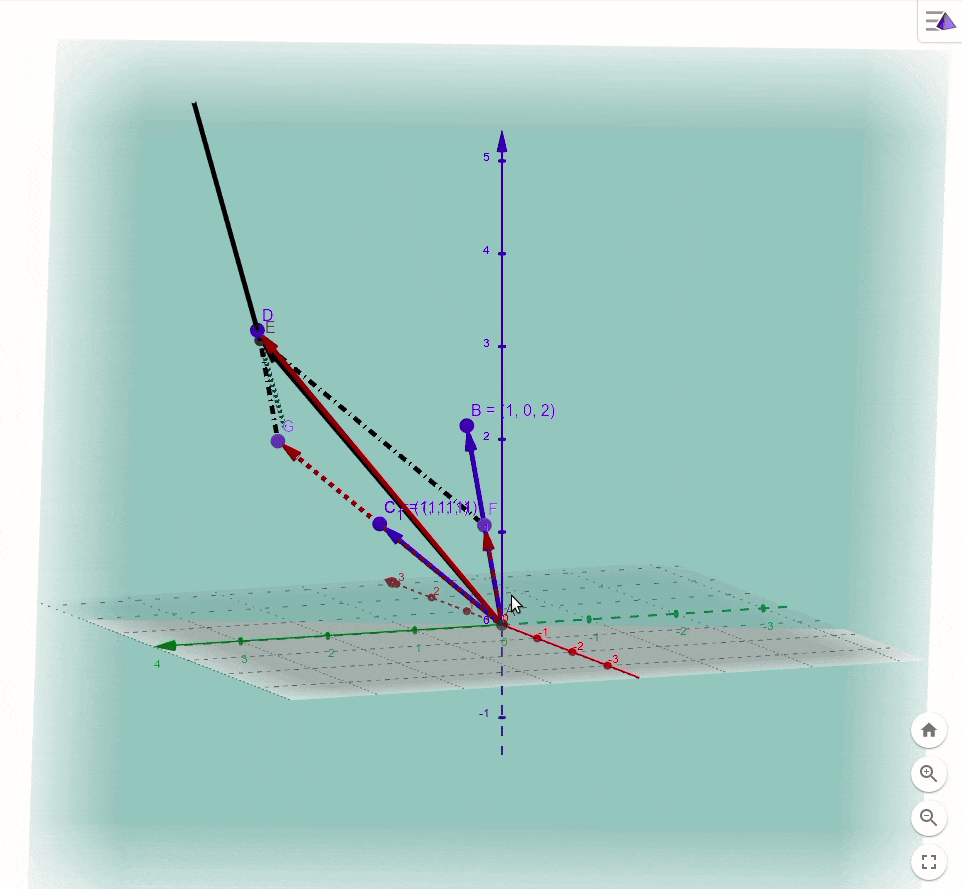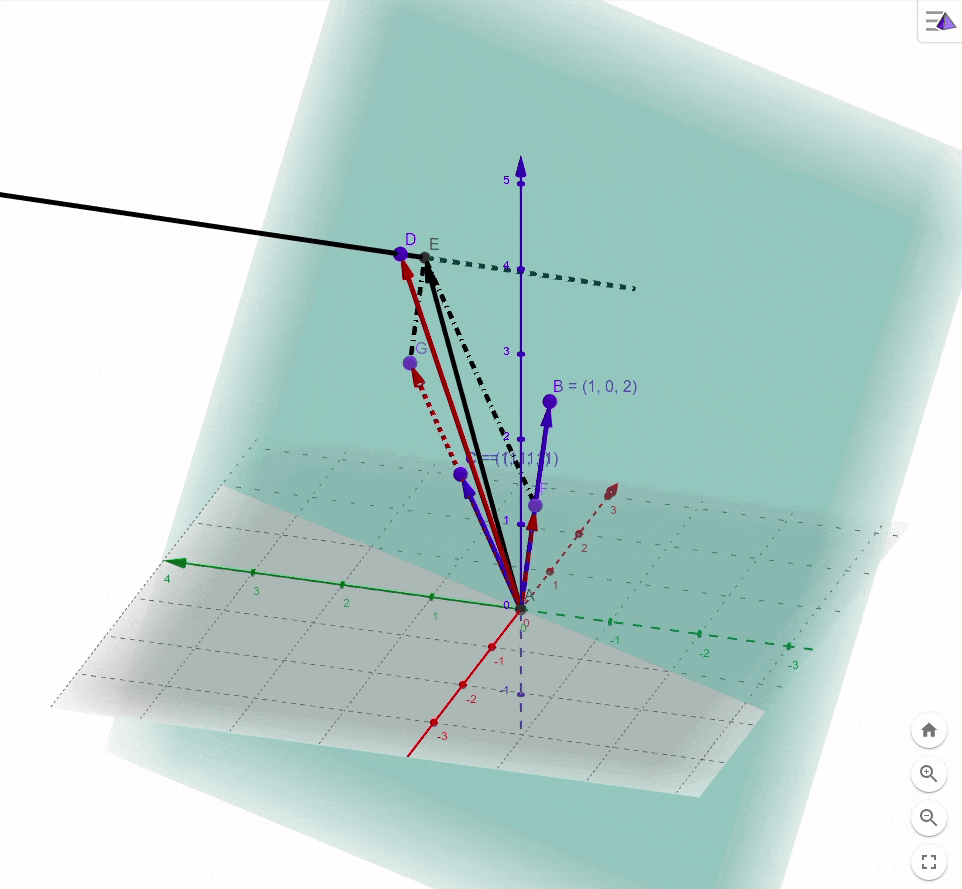
如图所示，$OE=b^{\prime },OD=b$,显而易见，$b^{\prime }$是$b$向此二维平面的正交投影，此时$b^{\prime }$和$b$之间的距离最近，距离差值维$DE$的长度。

而此时$b^{\prime }=x_1\ast a_1+x_2\ast a_2=x_{1}OC+x_{2}OB$，$x_1,x_2$就是我们需要求出的值。

更进一步的理解。当有n组数据带入时，A矩阵的维度将会是n×2.那么这里整个最小二乘拟合问题就可以理解成：$a_1,a_2$是n维线性空间中的两个线性无关的向量，在span{$a_1,a_2$}所张成的子空间中(2维)找到$b$在其中的正交投影$b^{\prime }$，二者之间的距离即是最小二乘优化的最小值min。$b^{\prime }$在基$a_1,a_2$上的投影，即是要求解的变量值,

如果需要拟合的变量不止2个，假设有m个，那么整个问题就可以理解成是n维向量到m维超平面的正交投影求解。

回到公式（3）中来，对其的求解，有以下方法。
$$\begin{gathered} Ax=b \\ {A}^{T}Ax=A^{T}b \\ x=(A^{T}A{)}^{-1}{A}^{T}b \end{gathered}$$
按照道理来说，此时我们已经解决问题了。但是众所周知，对于高维度的矩阵，计算机进行求逆操作是非常慢的，问题就出在实际应用中，点云地面的拟合，可能是几千上万个点，这样就会导致A矩阵的维度很高，显然直接求逆操作在此时是不可行的。所以，如何快速求解$Ax=b$是下一个要解决的问题，即SVD分解。

2 实际问题1：点云的地面拟合

2.1 解法1.分解协方差矩阵

其算法理论基于论文:Zermas, D., Izzat, I., & Papanikolopoulos, N. (2017). Fast segmentation of 3D point clouds: A paradigm on LiDAR data for autonomous vehicle applications. Proceedings - IEEE International Conference on Robotics and Automation, 5067–5073. https://doi.org/10.1109/ICRA.2017.7989591

求证：平面Ax+By+Cz+D=0的法向量为（A,B,C）.

证明：假设$(x_1,y_1,z_1),(x_2,y_2,z_2)$是当前平面上的两个点。

则有：$A{x}_1+B{y}_1+C{z}_1+D=0$,$A{x}_2+B{y}_2+C{z}_2+D=0$,所以两式相减，可得：

$A(x_1-x_2)+B(y_1-y_2)+C(z_1-z_2)=0$,即
$$\left[\begin{array}{ccc}A& B& C\end{array}\right]\left[\begin{array}{c}(x_1-x_2)\\ (y_1-y_2)\\ (z_1-z_2)\end{array}\right]=0$$
右边的矩阵表示平面上的任一点，且该式对平面上的任意两点都成立。

所以$n=(A,B,C)$即是所在平面的法向量。

对靠近地面的的n个点，计算其协方差矩阵。对协方差矩阵进行SVD分解，可以得到对应的特征值和特征向量。其中，最小特征值对应的特征向量就是地面平面的法向量。

目的：拟合地面所在的方程Ax+By+Cz+d=0

1. 取n个z值最小的点，认为其是地面点

取n个地面点，计算这n个点的协方差矩阵$Cov$，然后对其做SVD分解，得到其在各个分量。最小奇异值所对应的向量便是地面的法向量$n$.

由前面的证明可知：$n=(A，B，C)$

2. 对n个靠近地面的点遍历加和，计算一个均值$\bar{X}=(\bar{x},\bar{y},\bar{z})$。认为此均值带入地面所在方程
   $$\begin{gathered} A\bar{x}+B\bar{y}+C\bar{z}+D\approx 0 \\ 即：A\bar{x}+B\bar{y}+C\bar{z}\approx -D \end{gathered}$$

此时$-D$的值已知。

此时，均值$\bar{X}$因为是n个点的均值，默认是最靠近地面所在平面的点。其他所有的n个点，都可以认为更偏离所拟合的平面。即：
$$\begin{gathered} A\bar{x}+B\bar{y}+C\bar{z}+D\pm \delta \approx 0 \\ 即：A\bar{x}+B\bar{y}+C\bar{z}\approx -D\pm \delta \end{gathered}$$
因此，在对\velodyne_points中所有的topic进行筛选地面点的过程中，所有的点$X_i=(x_i,y_i,z_i)$带入式(3)所得到的值符合以下约束：
$$A{x}_i+B{y}_i+C{z}_i\in [-D-\delta ,-D+\delta ]$$
此时，$\delta$的值需要自己设定，代表了对地面点的筛选条件。

2.2 解法2 SVD 求解Ax=0

此方法类似于二维平面的直线拟合。

假设我们有$n$个($n>>4$)靠近地面的点，现假设地面平面所在的方程为$ax+by+cz+d=0$。利用这$n$个点对该平面方程的参数进行拟合。原理与二维平面的直线拟合类似，这里不做过多推导。

带入$n$个点的坐标，可得：
$$\{\begin{array}{l}a{x}_1+b{y}_1+c{z}_1+d=0\\ a{x}_2+b{y}_2+c{z}_2+d=0\\ a{x}_3+b{y}_3+c{z}_3+d=0\\ ...\\ a{x}_n+b{y}_n+c{z}_n+d=0\end{array}$$
即可化为以下$Ax=0$的齐次方程组形式(超定方程)。
$${\left[\begin{array}{cccc}{x}_1& y_1& z_1& 1\\ x_2& y_2& z_2& 1\\ & ...& & \\ x_n& y_n& z_n& 1\end{array}\right]}_{n\ast 4}{\left[\begin{array}{c}a\\ b\\ c\\ d\end{array}\right]}_{4\ast 1}=0$$
对矩阵$A$进行SVD即可得最后的结果。

问题：这种方法存在$[abcd]$的尺度问题。因为是齐次方程，其值可以任意缩放，带来的问题就是实际应用筛选地面点的过程中，不同的缩放系数会导致筛选阈值不确定性。这里建议根据实际分割效果做多次实验决定。

2.3 证明：SVD=最小二乘

$$\begin{gathered} D{P}_w=0 \\ 即Ax=0 \end{gathered}$$

$$\begin{gathered} D{P}_w=0 \\ 即Ax=0 \end{gathered}$$

下面以$Ax=0$这种更普遍的表达形式进行推导。

当$A_{m\ast n}$是一个超定方程的时候，此等式无解，因此需要取最小二乘的形式，即：
$$\begin{gathered} min||Ax|{|}_2^2 \\ =min(x^T{A}^{T}Ax） \\ sbj.||x||=1 \end{gathered}$$
已知:
$$\begin{gathered} A^{T}A=V\Lambda V^T \\ A=U\Sigma V^T,A^T=V{\Sigma }^T{U}^T \\ {U}^{T}U=V^{T}V=I \end{gathered}$$
可得，$V=[v_0{v}_1...v_n{]}_{n\ast n}$是$n$维空间里的标准正交基。所以$x_{n\ast 1}$可以由此标准正交基构成，即：
$$\begin{gathered} x=k_0{v}_0+k_1{v}_1+...+k_n{v}_n=\sum _{i=0}^n{k}_i{v}_i,x\in {\mathbb{R}}^n \\ sbj.||x||=1 \end{gathered}$$
由公式(12)可知:
$$\begin{gathered} A^{T}A=V{\Sigma }^T{U}^{T}U\Sigma V^T \\ =V{\Sigma }^T\Sigma V^T \\ =V\left[\begin{array}{ccc}{\sigma }_{max}^2& & \\ & \ddots & \\ & & {\sigma }_{min}^2\end{array}\right]V^T \end{gathered}$$
将(13)(14)带入到(11)中，
$$\begin{gathered} min=x^T[v_0...v_n]\left[\begin{array}{ccc}{\sigma }_{max}^2& & \\ & \ddots & \\ & & {\sigma }_{min}^2\end{array}\right]\left[\begin{array}{c}{v}_0^T\\ ...\\ v_n^T\end{array}\right]x \\ =x^T[v_0...v_n]\left[\begin{array}{ccc}{\sigma }_{max}^2{v}_0^T& & \\ & \ddots & \\ & & {\sigma }_{min}^2{v}_n^T\end{array}\right]x \\ =x^T\left[\begin{array}{ccc}{\sigma }_{max}^2{v}_0{v}_0^T& & \\ & \ddots & \\ & & {\sigma }_{min}^2{v}_n{v}_n^T\end{array}\right]x \\ =x^T\left[\begin{array}{ccc}{\sigma }_{max}^2& & \\ & \ddots & \\ & & {\sigma }_{min}^2\end{array}\right]x \\ =x^T\left[\begin{array}{ccc}{\sigma }_{max}^2& & \\ & \ddots & \\ & & {\sigma }_{min}^2\end{array}\right]x \\ =[k_0{v}_0...k_n{v}_n]\left[\begin{array}{ccc}{\sigma }_{max}^2& & \\ & \ddots & \\ & & {\sigma }_{min}^2\end{array}\right]\left[\begin{array}{c}{k}_0{v}_0^T\\ ...\\ k_n{v}_n^T\end{array}\right] \\ =k_0^2{\sigma }_{max}^2+...+k_n^2{\sigma }_{min}^2 \\ ={\sigma }_{min}^2 \end{gathered}$$

上述情况中，${\mathrm{k}}_n=1,{\mathrm{k}}_{\mathrm{i}}(i\ne n)=0$
此时，対应$x=k_n{v}_n=v_n$

3 实际问题2：三角化

假设世界中的某点$P_w$（世界坐标未知）被连续n帧相机数据观测到，像素坐标分别是$(u_1,v_1),...,(u_n,v_n)$.n帧对应的相机坐标$T_{wc1},...,T_{wcn}$,皆已知。根据三角化，我们可以构建最小二乘表达式，综合$n$帧观测数据，获得点$P_w$的位置。

预备推导：

$Pci$:$P_w$在第$i$帧相机坐标系$T_{wci}$下的坐标。

$P_{ci}=T_{cwi}{P}_w$

$$\begin{gathered} P_w=T_{wci}{P}_{ci} \\ =aa \end{gathered}$$

$P_{ci}=(x_{ci},y_{ci},z_{ci})=z_{ci}(\frac{x_{ci}}{z_{ci}},\frac{y_{ci}}{z_{ci}},1)=\lambda i(u_i,v_i,1)={\lambda }_i{p}_i$

其中，${\lambda }_i$是深度值，$p_i$是像素坐标

$$\begin{gathered} P_w=T_{wci}{P}_{ci} \\ {P}_w=T_{wci}{\lambda }_i{p}_i \\ {T}_{ciw}{P}_w={\lambda }_i{p}_i \end{gathered}$$

展开成矩阵的形式：
$$\begin{gathered} {\lambda }_i{\left[\begin{array}{c}{v}_i\\ u_i\\ 1\end{array}\right]}_{3\ast 1}={\left[\begin{array}{c}{\left[\begin{array}{c}{R}_{cw}\end{array}\right]}_{3\ast 3}[t_{cw}{]}_{3\ast 1}\end{array}\right]}_{3\ast 4}{P}_w \\ ={\left[\begin{array}{c}{\left[\begin{array}{c}{R}_{cw}\end{array}\right]}_{3\ast 3}[t_{cw}{]}_{3\ast 1}\end{array}\right]}_{3\ast 4}{\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]}_{4\ast 1} \\ ={\left[\begin{array}{cccc}{R}_{11}& R_{12}& R_{13}& t_1\\ R_{21}& R_{22}& R_{23}& t_2\\ R_{31}& R_{32}& R_{33}& t_3\end{array}\right]}_{3\ast 3}{\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]}_{4\ast 1} \end{gathered}$$
将其拆成行表示：
$$\begin{gathered} {\lambda }_i{u}_i=[R_1{t}_1]P_w=1\ast 4\ast 4\ast 1 \\ {\lambda }_i{v}_i=[R_2{t}_2]P_w=1\ast 4\ast 4\ast 1 \\ {\lambda }_i=[R_3{t}_3]P_w=1\ast 4\ast 4\ast 1 \\ 其中，R_1=[R_{11}{R}_{12}{R}_{13}],R_2,R_3一样 \end{gathered}$$
这里一共有4个未知数，分别是$P_w$的3个和一个${\lambda }_i$深度未知，将第三行带入到第一，二行，变成以下齐次方程的形式：
$$\begin{gathered} u_i[R_3{t}_3]P_w=[R_1{t}_1]P_w \\ {v}_i[R_3{t}_3]P_w=[R_2{t}_2]P_w \end{gathered}$$

$$\begin{gathered} u_i[R_3{t}_3]P_w-[R_1{t}_1]P_w=0 \\ {v}_i[R_3{t}_3]P_w-[R_2{t}_2]P_w=0 \end{gathered}$$

即：
$$\begin{gathered} (u_i[R_3{t}_3]-[R_1{t}_1]{)}_{1\ast 4}{P}_w=0 \\ (v_i[R_3{t}_3]-[R_2{t}_2]{)}_{1\ast 4}{P}_w=0 \end{gathered}$$
因此，可以将(7)中括号部分视作矩阵$D_{2\ast 4}$,即：
$$D_i{P}_w=0$$

注意D的维度是2×4，P是4×1，此时只是一组数据。所以当有n帧图像数据的时候，D的维度是2n×4.

接下来对D进行SVD分解
$$\begin{gathered} D^{T}D=U\Sigma V \\ =\sum _{i=1}^4{\sigma }_i^2{\mathbf{u}}_i{\mathbf{u}}_j^{\top } \\ 其中：D^T:4\ast 2n, \\ D:2n\ast 4. \\ U:4\ast 4, \\ V:4\ast 4, \\ \Sigma :4\ast 4 \\ {u}_i:4\ast 1, \\ {u}_j:1\ast 4. \end{gathered}$$
结论：$\Sigma$是奇异值处于对角线上的奇异值矩阵。其最小奇异值对应的v即是要求的解。

SVD的计算方法：https://byjiang.com/2017/11/18/SVD/

4 实际问题3：图像压缩&数据压缩

参考资料：https://www.zhihu.com/search?type=content&q=SVD

对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。

也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。

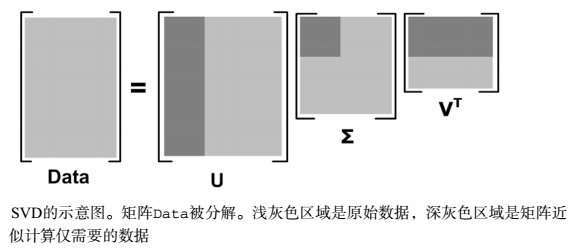
也就是说：
$$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^T\approx U_{m\times k}{\Sigma }_{k\times k}{V}_{k\times n}^T$$

由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。

    Mat image = imread("/home/alex/Pictures/earth.jpg", 0);
    Mat temp(image.size(), CV_32FC1, Scalar(0));
    image.convertTo(image, CV_32FC1);
    Mat U, W, V;
    SVD::compute(image, W, U, V,4);//opencv得到的V已经经过转置了
    Mat w(image.rows, image.cols, CV_32FC1, Scalar(0));
    int k = 90;
    float radio = (float)(1920 * 1080) / (float)(k*(1920 + 1080 + 1));//1920k 1080k k  分别是 U的行数乘保留的列数 + k个特征值 +V的列数乘k行

    for (int i = 0; i < k; i++)
        w.ptr<float>(i)[i] = W.ptr<float>(i)[0];

    cout << "U = " << U.cols << " U = " << U.rows << endl;
    cout << "w = " << w.cols << " w = " << w.rows << endl;
    cout << "V = " << V.cols << " V = " << V.rows << endl;

    temp = U*w*V;
    image.convertTo(image, CV_8UC1);
    temp.convertTo(temp, CV_8UC1);
    namedWindow("src",WINDOW_NORMAL);
    namedWindow("res",WINDOW_NORMAL);
    imshow("src",image);
    imshow("res",temp);
    waitKey(0);
    cout << "k = " << k << ",\t" << "radio = " << radio << endl;

输出：

rows: 1920 cols:1080
U = 1920 U = 1920
w = 1080 w = 1920
V = 1080 V = 1080
k = 90,	radio = 7.67744

对比如下：

原图:

处理后：

由此可以总结出：若一个像素为1字节, 原始图像需$m\ast n$字节的存储空间, 而使用SVD分解后只需$k\ast (m+n+1)$字节的存储空间, 以此达到压缩图像(矩阵)的目的.(k即是要保留的前k个最大的特征值)

水平有限，如有纰漏，请多指教