地址: https://arxiv.org/abs/2102.05013v1
内容:3D结构信息对分子处理十分重要,但是以往的GNN没有考虑到

- 先固定一个点
- 然后𝑑,𝜃,𝜑分别表示距离、夹角、扭角
- 因为直接使用这种三维结构缺乏有意义的物理表示,因此使用基于物理的表示进行处理
1 一般的基于3D的空间传递模型
- 对应公式




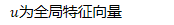




- 示意图,左边为更新边的(公式(1)第一个),右边为更新节点的(公式(1)第二个)
2 三维坐标的表示方法
- 三个重要的量:𝑑,𝜃,𝜑

3 提出的模型
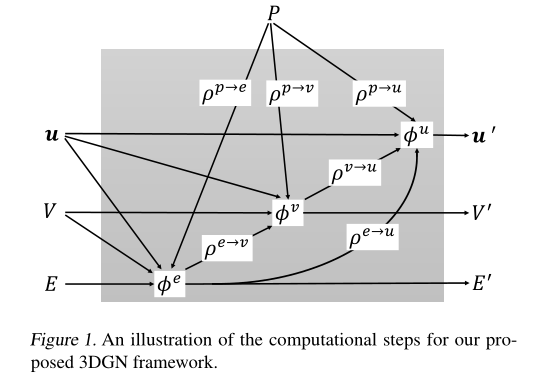
- 作者对图1进行了简化,结果如下
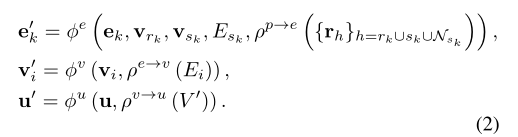
- 可以看出,空间信息的聚合只在更新边的时候使用了
空间信息的处理
- 这段看的完全一脸懵逼,看不懂,直接把最后三个公式当结论看了
- 由于直接使用(𝑑,𝜃,𝜑)没有物理上的意义,因此考虑近似密度泛函理论(DFT)的薛定谔方程的解
- 薛定谔方程可以用与时间无关的方式写成
- 通过分离变量并将笛卡尔坐标系转换为SCS(Griffiths&Schroeter,2018),SCS中薛定谔方程的一般正则解是
- 执行一些trick的简化版本
- 去掉扭角的简化版本
- 只有距离的简化版本
模型概览

4 实验结果
- 12项任务,8个最优,2个次优(表1),另外还有两个数据集也做了(表2~3)
- 消融实验
5 感想
- 总体来说还是很清晰的,除了那几个物理公式
- 最后的三维表表示,其实这就相当于用物理的方法,把先验知识引入到了模型之中。有效是肯定有效的,但是不见得就是最好的表示。个人觉得完全可以探讨一种预训练的方法,输入就是(𝑑,𝜃,𝜑),甚至是笛卡尔坐标,让模型自适应地进行调整。
















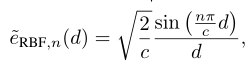




















 432
432

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








