9.4 多元复合函数的求导法则

 

第四节 多元复合函数的求导法则

引言

在本节中，我们将一元函数微分学中的复合函数的求导法则推广到多元复合函数的情形。多元复合函数的求导法则在多元函数微分学中也起着重要作用。我们将按照多元复合函数的不同复合情形，分三种情况进行讨论。

1. 一元函数与多元函数复合的情形

定理1

如果函数 𝑢=𝜑(𝑡)u=φ(t) 及 𝑣=𝜓(𝑡)v=ψ(t) 都在点 𝑡t 可导，函数 𝑧=𝑓(𝑢,𝑣)z=f(u,v) 在对应点 (𝑢,𝑣)(u,v) 具有连续偏导数，那么复合函数 𝑧=𝑓[𝜑(𝑡),𝜓(𝑡)]z=f[φ(t),ψ(t)] 在点 𝑡t 可导，且有：

证明

用同样的方法，可把定理推广到复合函数的中间变量多于两个的情形。例如，设 𝑧=𝑓[𝜑(𝑡),𝜓(𝑡),𝜔(𝑡)]z=f[φ(t),ψ(t),ω(t)] 则在与定理相类似的条件下，这复合函数在点 𝑡t 可导，且其导数可用下列公式计算：

在公式 (4-1) 及 (4-2) 中的导数称为全导数。

2. 多元函数与多元函数复合的情形

定理2

如果函数 𝑢=𝜑(𝑥,𝑦)u=φ(x,y) 及 𝑣=𝜓(𝑥,𝑦)v=ψ(x,y) 都在点 (𝑥,𝑦)(x,y) 具有对 𝑥x 及 𝑦y 的偏导数，函数 𝑧=𝑓(𝑢,𝑣)z=f(u,v) 在对应点 (𝑢,𝑣)(u,v) 具有连续偏导数，那么复合函数 𝑧=𝑓[𝜑(𝑥,𝑦),𝜓(𝑥,𝑦)]z=f[φ(x,y),ψ(x,y)] 在点 (𝑥,𝑦)(x,y) 的两个偏导数都存在，且有：

类似地，设 𝑢=𝜑(𝑥,𝑦)u=φ(x,y)、𝑣=𝜓(𝑥,𝑦)v=ψ(x,y) 及 𝑤=𝜔(𝑥,𝑦)w=ω(x,y) 都在点 (𝑥,𝑦)(x,y) 具有对 𝑥x 及 𝑦y 的偏导数，函数 𝑧=𝑓(𝑢,𝑣,𝑤)z=f(u,v,w) 在对应点 (𝑢,𝑣,𝑤)(u,v,w) 具有连续偏导数，则复合函数： 𝑧=𝑓[𝜑(𝑥,𝑦),𝜓(𝑥,𝑦),𝜔(𝑥,𝑦)]z=f[φ(x,y),ψ(x,y),ω(x,y)] 在点 (𝑥,𝑦)(x,y) 的两个偏导数都存在，且可用下列公式计算：

3. 其他情形

定理3

如果函数 𝑢=𝜑(𝑥,𝑦)u=φ(x,y) 在点 (𝑥,𝑦)(x,y) 具有对 𝑥x 及 𝑦y 的偏导数，函数 𝑣=𝜓(𝑦)v=ψ(y) 在点 𝑦y 可导，函数 𝑧=𝑓(𝑢,𝑣)z=f(u,v) 在对应点 (𝑢,𝑣)(u,v) 具有连续偏导数，那么复合函数

上述情形实际上是情形2的一种特例，即在情形2中，如变量 𝑣v 与 𝑥x 无关，从而 ∂𝑣∂𝑥=0∂x∂v​=0。在 𝑣v 对 𝑦y 求导时，由于 𝑣=𝜓(𝑦)v=ψ(y) 是一元函数，故换成普通导数 𝑑𝑣𝑑𝑦dydv​，这就得上述结果。

在情形3中，还会遇到这样的情形：复合函数的某些中间变量本身又是复合函数的自变量。例如，设 𝑧=𝑓(𝑢,𝑥,𝑦)z=f(u,x,y) 具有连续偏导数，而 𝑢=𝜑(𝑥,𝑦)u=φ(x,y) 具有偏导数，则复合函数 𝑧=𝑓[𝜑(𝑥,𝑦),𝑥,𝑦]z=f[φ(x,y),x,y] 可看做情形2中当 𝑣=𝑥v=x, 𝑤=𝑦w=y 的特殊情形。因此： 从而复合函数 𝑧=𝑓[𝜑(𝑥,𝑦),𝑥,𝑦]z=f[φ(x,y),x,y] 具有对自变量 𝑥x 及 𝑦y 的偏导数，且由公式 (4-5) 及 (4-6) 得：

实例

例1

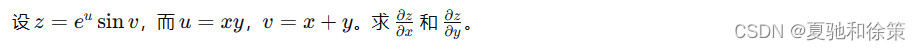
解：

例2

解：

例3

解：

总结

通过这些定理和例子，我们可以看到，复合函数的求导法则在多元函数微分学中是非常重要且实用的。无论是通过全导数还是偏导数，这些法则都帮助我们更好地理解和处理复杂的多元函数。