11.2 对坐标的曲线积分

11.2 对坐标的曲线积分

一、对坐标的曲线积分的概念与性质

变力沿曲线所作的功

我们知道，如果力 FFF 是恒力，且质点从 A 沿直线移动到 B，那么恒力 FFF 所作的功 WWW 等于向量 FFF 与向量 ABABAB 的数量积，即

现在 F(x,y)F(x,y)F(x,y) 是变力，且质点沿曲线 L 移动，功 WWW 不能直接按以上公式计算。然而，第一节中用来处理曲线形构件质量问题的方法，原则上也适用于目前的问题。

先用曲线弧 L 上的点 M1(x1,y1),M2(x2,y2),…,Mn−1(xn−1,yn−1)M_1(x_1, y_1), M_2(x_2, y_2), \ldots, M_{n-1}(x_{n-1}, y_{n-1})M1​(x1​,y1​),M2​(x2​,y2​),…,Mn−1​(xn−1​,yn−1​) 把 L 分成 n 个小弧段，取其中一个有向小弧段 Mi−1MiM_{i-1}M_iMi−1​Mi​ 来分析：由于 Mi−1MiM_{i-1}M_iMi−1​Mi​ 光滑而且很短，可以用有向线段

来近似代替它，其中 Δxi=xi−xi−1\Delta x_i = x_i - x_{i-1}Δxi​=xi​−xi−1​， Δyi=yi−yi−1\Delta y_i = y_i - y_{i-1}Δyi​=yi​−yi−1​。又由于函数 P(x,y)P(x,y)P(x,y) 与 Q(x,y)Q(x,y)Q(x,y) 在 L 上连续，可以用 Mi−1MiM_{i-1}M_iMi−1​Mi​ 上任意取定的一点 (ξi,ηi)(\xi_i, \eta_i)(ξi​,ηi​) 处的力

来近似代替这小弧段上各点处的力。这样，变力 F(x,y)F(x,y)F(x,y) 沿有向小弧段 Mi−1MiM_{i-1}M_iMi−1​Mi​ 所作的功 ΔWi\Delta W_iΔWi​ 可以认为近似地等于恒力 F(ξi,ηi)F(\xi_i, \eta_i)F(ξi​,ηi​) 沿 Mi−1MiM_{i-1}M_iMi−1​Mi​ 所作的功：

即

于是

用 λ\lambdaλ 表示 n 个小弧段的最大长度，令 λ→0\lambda \to 0λ→0 取上述和的极限，所得到的极限自然地被认作变力 FFF 沿有向曲线弧所作的功，即

这种和的极限在研究其他问题时也会遇到。现在引进下面的定义：

定义

设 Δxi=xi−xi−1\Delta x_i = x_i - x_{i-1}Δxi​=xi​−xi−1​， Δyi=yi−yi−1\Delta y_i = y_i - y_{i-1}Δyi​=yi​−yi−1​，点 (ξi,ηi)(\xi_i, \eta_i)(ξi​,ηi​) 为 Mi−1MiM_{i-1}M_iMi−1​Mi​ 上任意取定的点，作乘积

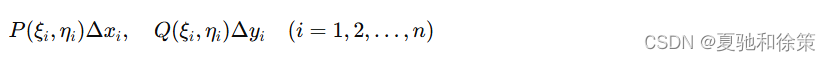
并作和。如果当各小弧段长度的最大值 λ→0\lambda \to 0λ→0 时，这和的极限总存在，且与曲线弧 L 的分法及点 (ξi,ηi)(\xi_i, \eta_i)(ξi​,ηi​) 的取法无关，那么称此极限为函数 P(x,y)P(x,y)P(x,y) 在有向曲线弧 L 上对坐标 xxx 的曲线积分，记作

类似地，如果总存在，且与曲线弧 L 的分法及点 (ξi,ηi)(\xi_i, \eta_i)(ξi​,ηi​) 的取法无关，那么称此极限为函数 Q(x,y)Q(x,y)Q(x,y) 在有向曲线弧 L 上对坐标 yyy 的曲线积分，记作

即

其中 P(x,y)P(x,y)P(x,y)、Q(x,y)Q(x,y)Q(x,y) 叫做被积函数，L 叫做积分弧段。

以上两个积分也称为第二类曲线积分。

在第二目中我们将看到，当 P(x,y)P(x,y)P(x,y) 与 Q(x,y)Q(x,y)Q(x,y) 在有向光滑曲线弧 L 上连续时，对坐标的曲线积分 ∫LP(x,y) dx\int_L P(x,y) \, dx∫L​P(x,y)dx 及 ∫LQ(x,y) dy\int_L Q(x,y) \, dy∫L​Q(x,y)dy 都存在。以后我们总假定 P(x,y)P(x,y)P(x,y) 与 Q(x,y)Q(x,y)Q(x,y) 在 L 上连续。

上述定义可以类似地推广到积分弧段为空间有向曲线弧 Γ\GammaΓ 的情形：

应用上经常出现的是

这种合并起来的形式，为简便起见，把上式写成

也可写成向量形式

或

类似地，把

简写成

或

其中 A(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k\mathbf{A}(x,y,z) = P(x,y,z)i + Q(x,y,z)j + R(x,y,z)kA(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k，dr=dxi+dyj+dzkd\mathbf{r} = dxi + dyj + dzkdr=dxi+dyj+dzk。如果 L（或 Γ\GammaΓ）是分段光滑的，我们规定函数在有向曲线弧 L（或 Γ\GammaΓ）上对坐标的曲线积分等于在光滑的各段上对坐标的曲线积分之和。

根据上述曲线积分的定义，可以导出对坐标的曲线积分的一些性质。为了表达简便起见，我们用向量形式表达，并假定其中的向量值函数在曲线 L 上连续。

性质1

设 α\alphaα 与 β\betaβ 为常数，则

性质2

若有向曲线弧 L 可分成两段光滑的有向曲线弧 L1L_1L1​ 和 L2L_2L2​，则

性质3

设 L 是有向光滑曲线弧，L‾\overline{L}L 是 L 的反向曲线弧，则

证明：把 L 分成 n 小段，相应的 L‾\overline{L}L 也分成 n 小段。对于每一个小弧段来说，当曲线弧的方向改变时，有向弧段在坐标轴上的投影，其绝对值不变，但要改变符号，因此性质3成立。

性质3 表示，当积分弧段的方向改变时，对坐标的曲线积分要改变符号。因此关于对坐标的曲线积分，我们必须注意积分弧段的方向。

这一性质是对坐标的曲线积分所特有的，对弧长的曲线积分不具有这一性质。而对弧长的曲线积分所具有的性质，对坐标的曲线积分也不具有类似的性质。

二、对坐标的曲线积分的计算法

定理：曲线积分的计算

设 P(x,y)P(x,y)P(x,y) 与 Q(x,y)Q(x,y)Q(x,y) 在有向曲线弧 LLL 上有定义且连续，LLL 的参数方程为 x=ϕ(t),y=ψ(t)x = \phi(t), \quad y = \psi(t)x=ϕ(t),y=ψ(t) 当参数 ttt 单调地由 α\alphaα 变到 β\betaβ 时，点 M(x,y)M(x,y)M(x,y) 从 LLL 的起点 AAA 沿 LLL 运动到终点 BBB。若 ϕ(t)\phi(t)ϕ(t) 与 ψ(t)\psi(t)ψ(t) 在以 α\alphaα 及 β\betaβ 为端点的闭区间上具有一阶连续导数，且 存在，且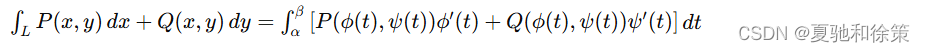

证明

在 LLL 上取一列点 A=M0,M1,M2,…,Mn−1,Mn=BA = M_0, M_1, M_2, \ldots, M_{n-1}, M_n = BA=M0​,M1​,M2​,…,Mn−1​,Mn​=B 它们对应于一列单调变化的参数值

根据对坐标的曲线积分的定义，有

设点 (ξi,ηi)(\xi_i, \eta_i)(ξi​,ηi​) 对应于参数值 τi\tau_iτi​，即 ξi=ϕ(τi)\xi_i = \phi(\tau_i)ξi​=ϕ(τi​)， ηi=ψ(τi)\eta_i = \psi(\tau_i)ηi​=ψ(τi​)，这里 τi\tau_iτi​ 在 ti−1t_{i-1}ti−1​ 与 tit_iti​ 之间。由于 应用微分中值定理，有 Δxi=ϕ′(τi)Δti\Delta x_i = \phi'(\tau_i) \Delta t_iΔxi​=ϕ′(τi​)Δti​ 其中 之间。于是

因为函数 ϕ′(t)\phi'(t)ϕ′(t) 在闭区间 [α,β][ \alpha, \beta ][α,β]（或 [β,α][ \beta, \alpha ][β,α]）上连续，我们可以把上式中的 τi\tau_iτi​ 换成 ttt，从而

由于函数 P(ϕ(t),ψ(t))ϕ′(t)P(\phi(t), \psi(t)) \phi'(t)P(ϕ(t),ψ(t))ϕ′(t) 连续，这个定积分是存在的，因此上式左端的曲线积分存在，并且有

同理可证

把以上两式相加，得

参数方程形式的曲线积分

公式(2-1)表明，计算对坐标的曲线积分 时，只要把 xxx、yyy、dxdxdx、dydydy 依次换为 ϕ(t)\phi(t)ϕ(t)、ψ(t)\psi(t)ψ(t)、ϕ′(t)dt\phi'(t) dtϕ′(t)dt、ψ′(t)dt\psi'(t) dtψ′(t)dt，然后从 LLL 的起点所对应的参数值 α\alphaα 到 LLL 的终点所对应的参数值 β\betaβ 作定积分就行了。这里必须注意，下限 α\alphaα 对应于 LLL 的起点，上限 β\betaβ 对应于 LLL 的终点，α\alphaα 不一定小于 β\betaβ。

特殊情形：由方程 y=ψ(x)y = \psi(x)y=ψ(x) 或 x=ϕ(y)x = \phi(y)x=ϕ(y) 给出的曲线

如果 LLL 由方程 y=ψ(x)y = \psi(x)y=ψ(x) 或 x=ϕ(y)x = \phi(y)x=ϕ(y) 给出，可以看做参数方程的特殊情形。例如，当 LLL 由 y=ψ(x)y = \psi(x)y=ψ(x) 给出时，公式(2-1)成为 这里下限 aaa 对应 LLL 的起点，上限 bbb 对应 LLL 的终点。

空间曲线的推广

公式(2-1)可推广到空间曲线 Γ\GammaΓ 由参数方程 给出的情形，这样便得到 这里下限 α\alphaα 对应 Γ\GammaΓ 的起点，上限 β\betaβ 对应 Γ\GammaΓ 的终点。

三、对坐标的曲线积分的例题

解法一：将所给积分化为对 xxx 的定积分来计算。

由于 y=±xy = \pm \sqrt{x}y=±x​ 不是单值函数，所以要把 LLL 分为 A0A0A0 和 OBOBOB 两部分。在 A0A0A0 上，y=−xy = -\sqrt{x}y=−x​，xxx 从 1 变到 0；在 OBOBOB 上，y=xy = \sqrt{x}y=x​，xxx 从 0 变到 1。因此，

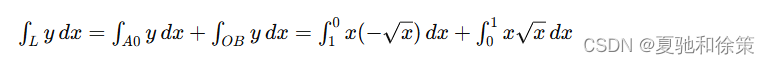
计算：

解法二：将所给积分化为对 yyy 的定积分来计算。

现在 x=y2x = y^2x=y2，yyy 从 -1 变到 1。因此，

1. 半径为 aaa、圆心为原点、按逆时针方向绕行的上半圆周；
2. 从点 A(a, 0) 沿 x 轴到点 B(-a, 0) 的直线段。

解 (1)：

LLL 的参数方程为 x=acos⁡θ,y=asin⁡θx = a \cos \theta, \quad y = a \sin \thetax=acosθ,y=asinθ 当参数 θ\thetaθ 从 0 变到 π\piπ 的曲线弧。因此，

由于

计算得：

所以，

解 (2)：

LLL 的方程为 y=0y = 0y=0，xxx 从 aaa 变到 −a-a−a。所以，

从例 2 看出，虽然两个曲线积分的被积函数相同，起点和终点也相同，但沿不同路径得出的积分值并不相等。

1. 抛物线 y=x2y = x^2y=x2 上从 O(0,0) 到 B(1,1) 的一段弧；
2. 抛物线 x=y2x = y^2x=y2 上从 O(0,0) 到 B(1,1) 的一段弧；
3. 有向折线 OAB，这里 O, A, B 依次是点 (0,0), (1,0), (1,1)。

解 (1)：化为对 xxx 的定积分。

解 (2)：化为对 yyy 的定积分。

解 (3)：

在 OAOAOA 上，y=0y = 0y=0，xxx 从 0 变到 1，所以，

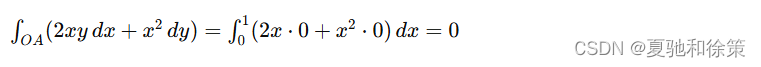
在 ABABAB 上，x=1x = 1x=1，yyy 从 0 变到 1，所以，

从而，

从例 3 可以看出，虽然沿不同路径，曲线积分的值可以相等。

解：

直线段 AB 的方程是 x3=y2=z\frac{x}{3} = \frac{y}{2} = z3x​=2y​=z 化为参数方程得

所以，

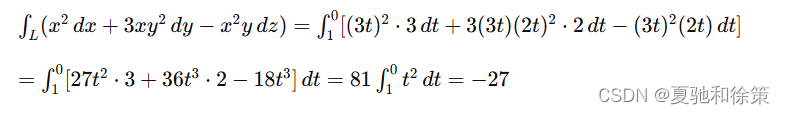
例 5

解：

利用椭圆的参数方程 x=acos⁡tx = a \cos tx=acost，y=bsin⁡ty = b \sin ty=bsint，ttt 从 0 变到 π2\frac{\pi}{2}2π​。于是

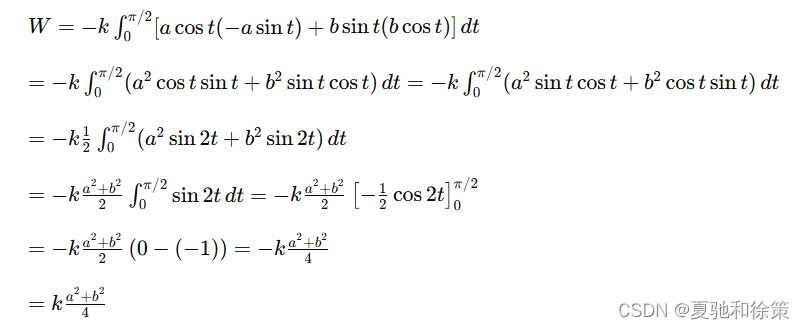
综上所述，力 FFF 所作的功

三、两类曲线积分之间的联系

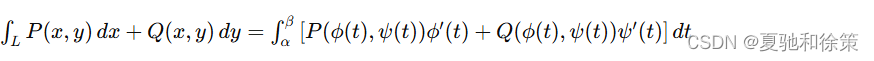
我们知道，向量 T=ϕ′(t)i+ψ′(t)jT = \phi'(t)i + \psi'(t)jT=ϕ′(t)i+ψ′(t)j 是曲线弧 LLL 在点 M(ϕ(t),ψ(t))M(\phi(t), \psi(t))M(ϕ(t),ψ(t)) 处的一个切向量，它的指向与参数 ttt 的增长方向一致。当 α<β\alpha < \betaα<β 时，这个指向就是有向曲线弧 LLL 的方向。以后，我们称这种指向与有向曲线弧的方向一致的切向量为有向曲线弧的切向量。于是，有向曲线弧 LLL 的切向量为

它的方向余弦为

由对弧长的曲线积分的计算公式可得

由此可见，平面曲线弧 LLL 上的两类曲线积分之间有如下联系：

其中 α(x,y)\alpha(x, y)α(x,y) 与 β(x,y)\beta(x, y)β(x,y) 为有向曲线弧 LLL 在点 (x,y)(x, y)(x,y) 处的切向量的方向角。类似地可知，空间曲线弧 Γ\GammaΓ 上的两类曲线积分之间有如下联系：

两类曲线积分之间的联系也可用向量的形式表达，例如，空间曲线弧 Γ\GammaΓ 上的两类曲线积分之间的联系可写成如下形式：

或