卡尔曼滤波02

这节课主要内容就是介绍连续随机系统的离散化、连续时间KF和噪声相关的卡尔曼滤波，更多的是一个公式推导，这里就不过多介绍，仅给一个最终结果。

1 连续随机系统的离散化与连续时间KF

1.1 连续时间方程系统离散化

连续时间方程

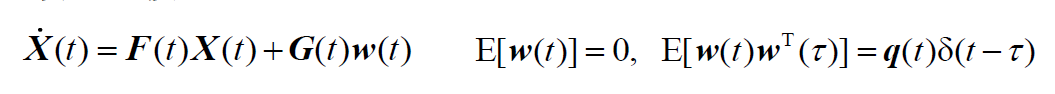
离散化后的形式

其中：

最终离散化结论


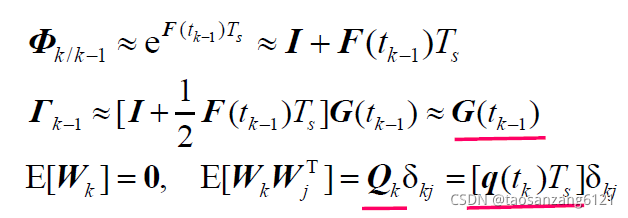
一些简单的随机过程离散化

1.2 量测方差离散化

量测方程

离散化结果


观测噪声方差阵与离散化间隔有关系，离散化间隔越小，等效的方差应该越大。

1.3 连续时间卡尔曼滤波

连续时间卡尔曼滤波是个微分方程，获得连续时间卡尔曼滤波结果需要解这个微分方程（矩阵黎卡蒂(Riccati)方程）。

2 噪声条件下相关的卡尔曼滤波

卡尔曼滤波噪声分为系统噪声和量测噪声，下面就分别讨论他们之间互相相关时的处理方法

2.1 系统噪声与量测噪声相关

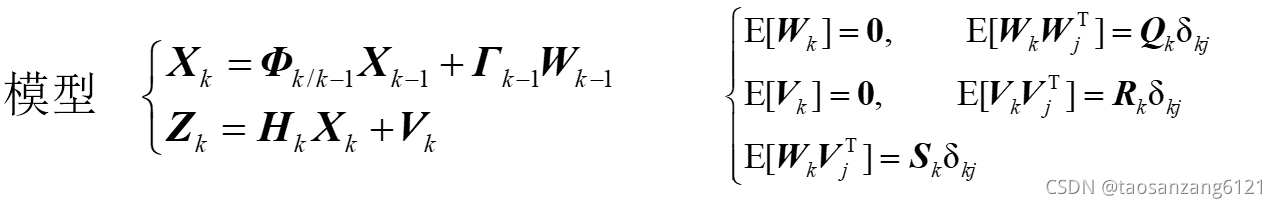
可以将状态方程改写为

其中J是个待求矩阵。为求这个矩阵对新的系统噪声W进行分析，此时系统噪声与量测噪声的关系是如下式，两者无关需要其等于0，求得J的前提是必须准确知道S，实际情况中S很难获得，所以一般都认为系统噪声与量测噪声不相关。


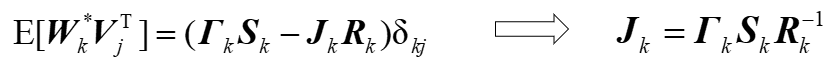
新系统噪声为：

其滤波过程可以总结为：

由上可知，当前时刻是由上一时刻推过来的，因为必须有两次观测才能得到结果。

2.2 系统噪声为有色噪声

系统噪声为有色噪声处理的前提条件是有色部分必须可以建模
此时的处理方式为，对有色噪声进行建模，将其作为参数进行估计

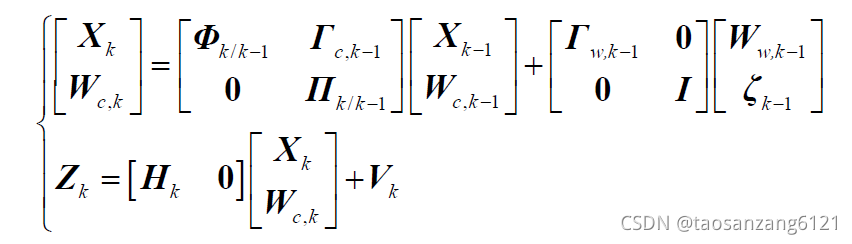
可以得到滤波模型

2.3 量测噪声为有色噪声

在实际情况下其实用白噪声去对其进行建模，其结果相差不了多少，不需要考虑是否有色。

此时有两种解决方法

方法一：与2.2一样对噪声建模

通过画红线的地方可以看出此时系统噪声和量测噪声是相关的，要再参考2.1中去相关

方法二 测量求差法

观测噪声模型为：

前后相邻历元量测求差

上式的后半部分则是新的量测噪声，是个白噪声。最后得到模型：