卡尔曼滤波04_2 Sage-Husa自适应滤波

Sage-Husa自适应滤波

自适应滤波的状态空间模型为：


自适应滤波适用的系统为噪声和噪声的方差未知，且不是零均值。由于噪声未知，噪声参数的不准确可能会影响系统输出，此时自适应滤波采用一边进行参数估计一边进行状态识别来处理。
自适应滤波的原则：噪声均值均可等效于状态增广（作为参数进行估计），激励噪声方差难以自适应，量测噪声方差相对容易自适应（可观测性更强的系统，才适用于自适应滤波），应尽量减少噪声自适应参数的数目。
量测噪声的自适应方法：


观测噪声方差R未知，由上式可以表示为：

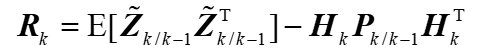
上式是一种统计的满足，用时间平均来估计R

上式为一种等加权平均，但随着时间的增长，1/k区域0，则随着时间的增长其自适应能力越差，因此可以采用一种指数渐消记忆的方法：


渐消因子的确定方式就是自己不断的尝试，一般的取值都是0.9,0.99等比较接近于1的数。
当实际噪声比较小时，容易出现量测方差负定，可改用“序贯量测+方差受限”自适应方法加以解决：



自适应滤波过程就如下图所示：

普通的卡尔曼滤波滤波计算回路与增益计算回路之间是独立的，只有增益计算回路中的增益矩阵用于滤波计算回路（紫色箭头），但是自适应中的R受观测值影响（红色箭头），所以自适应滤波系统是一个复杂的非线性系统，系统的稳定性难以证明，只能通过仿真来测试。