本文讨论的关键词:Logistic Regression(逻辑回归)、Neural Networks(神经网络)
之前在学习LR和NN的时候,一直对它们独立学习思考,就简单当做是机器学习中的两个不同的models,从来没有放在一起观察过,最近通过阅读网络资料,才发现,原来LR和NN之间是有一定的联系的,了解它们之间的联系后,可以更好地理解
Logistic Regression(逻辑回归)和Neural Networks(神经网络)
- Logistic Regression:典型的二值分类器,用来处理两类分类问题,当然,也可以用来处理多类问题,但要转换为One-vs-All或者是One-vs-One问题;Andrew Ng的机器学习课程中有对此的详细介绍
- 专门用来进行多类分类问题的多维逻辑回归器为:
Softmax regression / multinomial Logistic Regression; - 虽然逻辑回归器有许多的kernelized variants,但standard model(即最原始的LR)是一个线性分类器,主要用来处理数据集为more or less线性可分的情况;
- 专门用来进行多类分类问题的多维逻辑回归器为:
- Neural Networks:神经网络,由多个神经元构造,可以有多个输入、多个输出
Logistic Regression(逻辑回归)和Neural Networks(神经网络)之间到底有什么关系呢?
Logistic Regression
Basically, we can think of logistic regression as a one layer neural network.
实际上,可以将Logistic Regression看做是仅含有一个神经元的单层的神经网络!
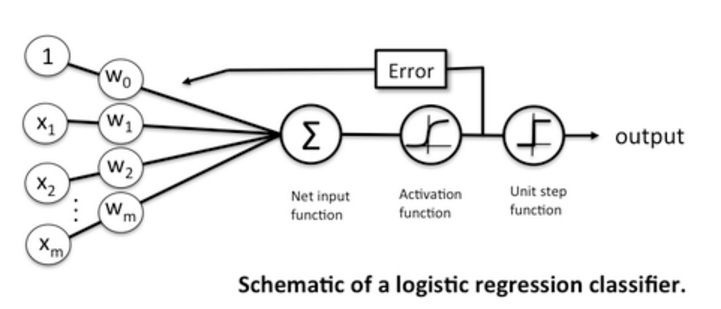
- 下面以图例的方式给出了Logistic Regression的结构,该图清晰地展示了Logistic Regression的结构
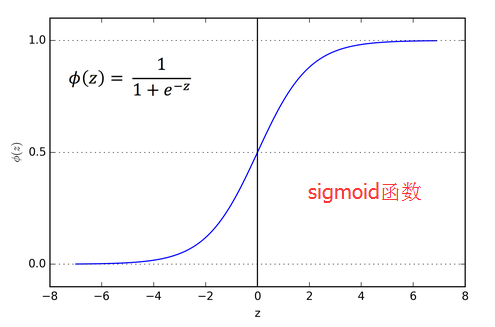
图中的Activation function为sigmoid function(也称为logistic activation functions),该激活函数的示意图如下:
- 从该图中可以看到,LR结构图的前半部分(不包含step function的部分,如下图红框所示)其实就是一个简单的神经元模型(关于神经网络的介绍见下文)
- 上图中绿色框中的部分为LR的threshold function(这里使用了step function),用来对前面激活函数的输出进行相应的阈值处理,从而实现两类分类问题(例如,threshold function函数输出为0时,对应类1,threshold function函数输出为1时,对应类2)
Softmax regression
Softmax regression其实是多维的Logistic regression,它其实可以看做是单层多个神经元的神经网络!
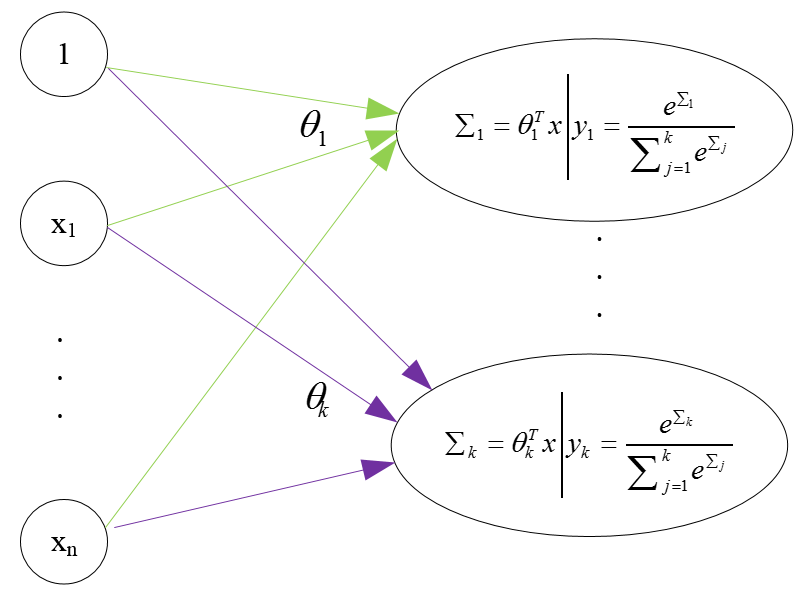
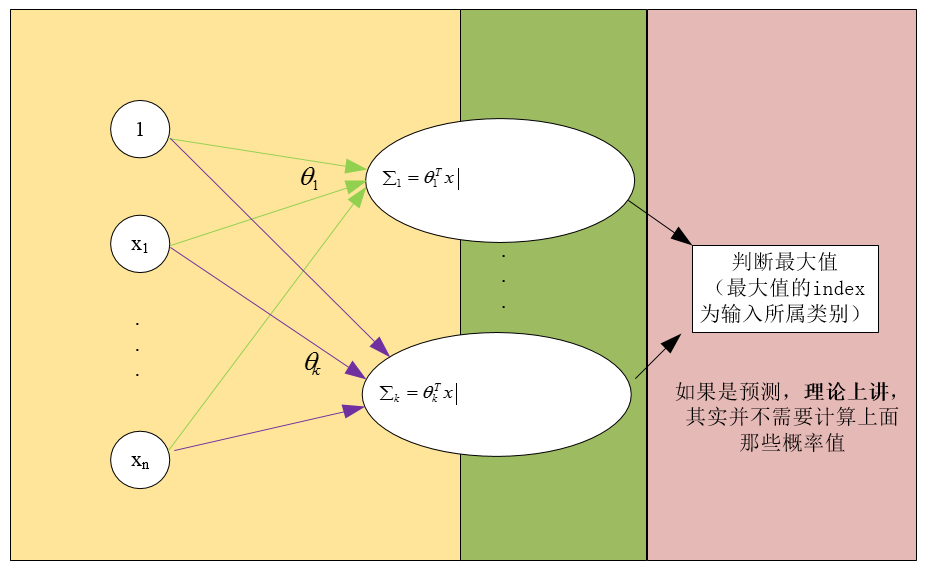
下图给出了softmax regression的基本结构,可以看到,其实,softmax regression可以看做是含有k个神经元的一层神经网络,
这里应该注意到:
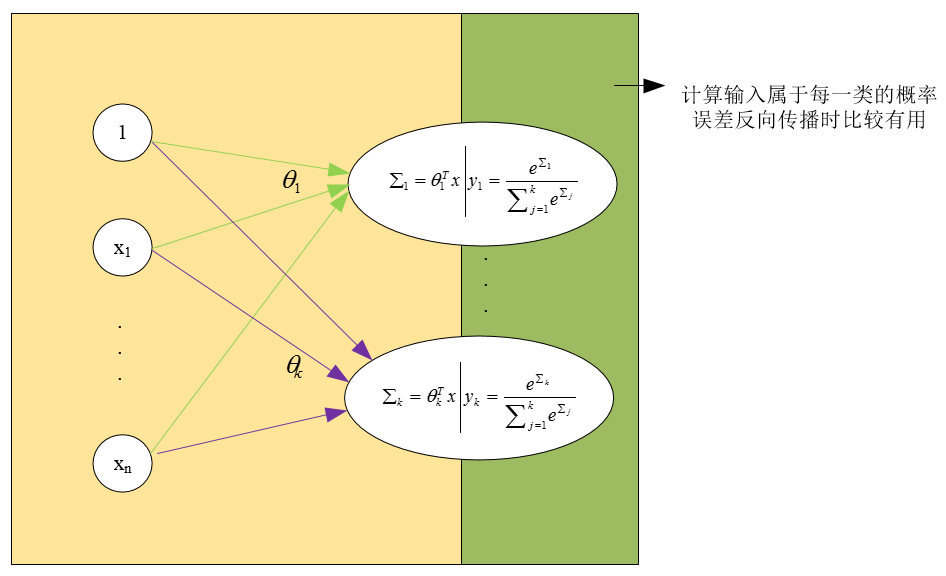
- 如果仅仅是要进行类别的预测,那么,只需要计算到sigma即可,不需要再求后面的softmax函数(上图所示的函数,注意,它与logistic regression中用到的sigmoid函数是不同的)
- 使用softmax函数,只是为了使输出具有概率意义,并且,有利于利用训练集去学习网络的权值;也可以这样理解,其实,softmax function只是在train的时候比较有用,利用它学习完网络参数后,在做predict的时候,其实就不需要它了(因为它是增函数)
神经网络的激活函数
神经元对应的激活函数
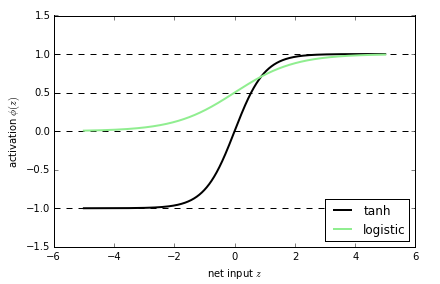
在神经网络中,神经元的激活函数多用sigmoid function,上面提到的logistic regression也用到了该函数,但实际上,另外一个激活函数:tanh函数的效果要比sigmoid函数好些,因为tanh函数并不会将神经元的输出局限于大于0,tanh的函数输出值区间为[-1,1]
tanh = the hyperbolic tangent
仍考虑具有sigmoid fucntion的神经元:logistic regression的一个优点是logistic cost fucntion (or max-entropy) 是一个凸函数,可以求得全局最小值。
关于神经网络的代价函数
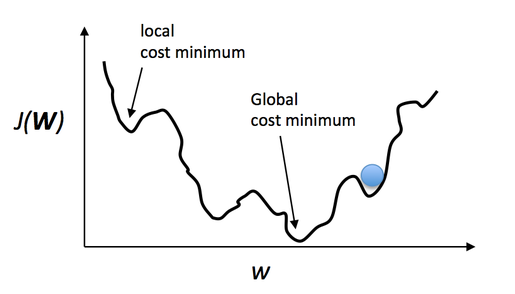
但是,对于神经网络而言,由于它将多个sigmoid function连接在一起了,这种凸函数的性质将不存在了。对于仅含有一个权值的多层神经网络(认为其他权值都为已知),它的cost function也具有非常崎岖的性质,如下图所示,可以看到,该cost function具有多个局部最小值
实际应用中,对于仅含有一个或者两个隐藏层的神经网络而言,它的cost function虽然是非凸的,但是利用误差反向传播算法,可以得到还不错的效果,虽然可能得到的是个局部极小值(a local minima),但分类效果还是不错的。





 本文探讨逻辑回归(LR)与神经网络(NN)之间的联系。LR可视为单层神经网络,其激活函数通常为sigmoid。Softmax回归是多维逻辑回归,可视为单层多神经元的NN。NN的激活函数除sigmoid外,还包括tanh。虽然LR的cost函数是凸的,但多层NN的cost函数非凸,可能导致局部最小值。
本文探讨逻辑回归(LR)与神经网络(NN)之间的联系。LR可视为单层神经网络,其激活函数通常为sigmoid。Softmax回归是多维逻辑回归,可视为单层多神经元的NN。NN的激活函数除sigmoid外,还包括tanh。虽然LR的cost函数是凸的,但多层NN的cost函数非凸,可能导致局部最小值。

















:逻辑回归和神经网络之间有什么关系?&spm=1001.2101.3001.5002&articleId=51547428&d=1&t=3&u=e1494eea4e764dd9a3bf167b975db806)
 2581
2581










