K-近邻算法（KNN）

有这样一句谚语：“如果走路像鸭子，叫声也像鸭子，长得还像鸭子，那么它很可能就是一只鸭子。”用一幅图来生动表示：

KNN原理形象图

KNN分类基本思想是：

• 计算待分类样品到每个训练样例的距离；
• 取距离最近的K个训练集样例；
• K个样品中哪个类别的训练样例占多数，则待分类元组就属于哪个类别。

KNN数学描述：

1. 把每个样例看作n维空间上的一个数据点，n是属性个数。
2. 对给定的测试样例z，计算其与训练集中其他数据点的距离（邻近度）。

样本点x和y之间的距离采用欧式距离：

       或曼哈顿距离：

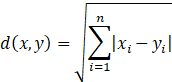
3.然后找出和z距离最近的K个数据点，将z分配到其最近邻的多数类。

KNN算法流程图：

最关键的参数就是K值，K值太小，预测结果不准且容易变动；K值太大，可能会误分。实践中，往往通过若干次实验来确定K值，取分类误差率最小的K值。

KNN算法优缺点：

①优点：

1. 通过施加距离权重（如权值与距离成反比），可以较好避免样本不平衡问题；
2. 算法简单，易于理解及实现。

②缺点：

1. 计算量较大，但可以通过对样本点剪辑或对样本分群分层来优化；
2. 对样本容量较小的分类容易产生误分。