文章目录
Image Deformation Using Moving Least Squares移动最小二乘
1.意义
移动最小二乘的移动是指, 所有traindata 对 每个grid point的影响(weight)是不一样的, 因此每个位置都对应一个不同的仿射变换。
2.变换方式
文中介绍三种变换: 仿射,相似,刚体变换
3.对应的代码:
https://github.com/Jarvis73/Moving-Least-Squares 实现了三种变换,但是结果与的代码molesq(https://github.com/clbarnes/molesq)不一致
另外我自己实现了仿射变换与 molesq是一致的。
3.1. 方法一
修改自(https://github.com/Jarvis73/Moving-Least-Squares)
import cv2
import numpy as np
from matplotlib import pyplot as plt
from molesq import Transformer
from my_mls_affine_deformation import mls_affine_my
from my_mls_affine_deformation_molesq import show_flow_im, flow_warp
np.seterr(divide='ignore', invalid='ignore')
def mls_affine_deformation_my(vy, vx, p, q, alpha=1.0, eps=1e-8):
"""
Affine deformation
Parameters
----------
vy, vx: ndarray
coordinate grid, generated by np.meshgrid(gridX, gridY)
p: ndarray
an array with size [n, 2], original control points, in (y, x) formats
q: ndarray
an array with size [n, 2], final control points, in (y, x) formats
alpha: float
parameter used by weights
eps: float
epsilon
Return
------
A deformed image.
"""
# Change (x, y) to (row, col)
q = np.ascontiguousarray(q.astype(np.float32))
p = np.ascontiguousarray(p.astype(np.float32))
# Exchange p and q and hence we transform destination pixels to the corresponding source pixels.
p, q = q, p
grow = vx.shape[0] # grid rows
gcol = vx.shape[1] # grid cols
ctrls = p.shape[0] # control points
# Precompute
reshaped_p = p.reshape(ctrls, 2, 1, 1) # [ctrls, 2, 1, 1]
reshaped_v = np.vstack((vx.reshape(1, grow, gcol), vy.reshape(1, grow, gcol))) # [2, grow, gcol]
w = 1.0 / (np.sum((reshaped_p - reshaped_v).astype(np.float32) ** 2, axis=1) + eps) ** alpha # [ctrls, grow, gcol]
w /= np.sum(w, axis=0, keepdims=True) # [ctrls, grow, gcol]
pstar = np.zeros((2, grow, gcol), np.float32)
for i in range(ctrls):
pstar += w[i] * reshaped_p[i] # [2, grow, gcol]
phat = reshaped_p - pstar # [ctrls, 2, grow, gcol]
phat = phat.reshape(ctrls, 2, 1, grow, gcol) # [ctrls, 2, 1, grow, gcol]
phat1 = phat.reshape(ctrls, 1, 2, grow, gcol) # [ctrls, 1, 2, grow, gcol]
reshaped_w = w.reshape(ctrls, 1, 1, grow, gcol) # [ctrls, 1, 1, grow, gcol]
pTwp = np.zeros((2, 2, grow, gcol), np.float32)
for i in range(ctrls):
pTwp += phat[i] * reshaped_w[i] * phat1[i]
del phat1
try:
inv_pTwp = np.linalg.inv(pTwp.transpose(2, 3, 0, 1)) # [grow, gcol, 2, 2]
flag = False
except np.linalg.linalg.LinAlgError:
flag = True
det = np.linalg.det(pTwp.transpose(2, 3, 0, 1)) # [grow, gcol]
det[det < 1e-8] = np.inf
reshaped_det = det.reshape(1, 1, grow, gcol) # [1, 1, grow, gcol]
adjoint = pTwp[[[1, 0], [1, 0]], [[1, 1], [0, 0]], :, :] # [2, 2, grow, gcol]
adjoint[[0, 1], [1, 0], :, :] = -adjoint[[0, 1], [1, 0], :, :] # [2, 2, grow, gcol]
inv_pTwp = (adjoint / reshaped_det).transpose(2, 3, 0, 1) # [grow, gcol, 2, 2]
mul_left = reshaped_v - pstar # [2, grow, gcol]
reshaped_mul_left = mul_left.reshape(1, 2, grow, gcol).transpose(2, 3, 0, 1) # [grow, gcol, 1, 2]
mul_right = np.multiply(reshaped_w, phat, out=phat) # [ctrls, 2, 1, grow, gcol]
reshaped_mul_right = mul_right.transpose(0, 3, 4, 1, 2) # [ctrls, grow, gcol, 2, 1]
out_A = mul_right.reshape(2, ctrls, grow, gcol, 1, 1)[0] # [ctrls, grow, gcol, 1, 1]
A = np.matmul(np.matmul(reshaped_mul_left, inv_pTwp), reshaped_mul_right, out=out_A) # [ctrls, grow, gcol, 1, 1]
A = A.reshape(ctrls, 1, grow, gcol) # [ctrls, 1, grow, gcol]
del mul_right, reshaped_mul_right, phat
# Calculate q
reshaped_q = q.reshape((ctrls, 2, 1, 1)) # [ctrls, 2, 1, 1]
qstar = np.zeros((2, grow, gcol), np.float32)
for i in range(ctrls):
qstar += w[i] * reshaped_q[i] # [2, grow, gcol]
del w, reshaped_w
# Get final image transfomer -- 3-D array
transformers = np.zeros((2, grow, gcol), np.float32)
for i in range(ctrls):
transformers += A[i] * (reshaped_q[i] - qstar)
transformers += qstar
del A
# Correct the points where pTwp is singular
if flag:
blidx = det == np.inf # bool index
transformers[0][blidx] = vx[blidx] + qstar[0][blidx] - pstar[0][blidx]
transformers[1][blidx] = vy[blidx] + qstar[1][blidx] - pstar[1][blidx]
# Removed the points outside the border
# transformers[transformers < 0] = 0
# transformers[0][transformers[0] > grow - 1] = 0
# transformers[1][transformers[1] > gcol - 1] = 0
return transformers#.astype(np.int16)
def cal_affine_flow(img, p, q, alpha=1):
'''
返回img大小的flow, 从p转换到q
p, q是转换前后的坐标点
Parameters
----------
img:
p: (x, y) format
q: (x, y) format
Returns
-------
'''
p = p[..., ::-1]
q = q[..., ::-1]
h, w = img.shape[:2]
xx, yy = np.meshgrid(np.arange(w), np.arange(h))
affine = mls_affine_deformation_my(xx, yy, p, q, alpha)
f1 = np.dstack((xx, yy)).reshape(h, w, 2).astype(np.float32)
f2 = np.array(affine).transpose(1, 2, 0).reshape(h, w, 2)[..., ::-1].astype(np.float32)
flow = f1 - f2
flow = flow.astype(np.float32)
return flow
3.2. 方法二
我自己的实现:
def mls_affine_my(image, p, q):
'''
其实给定p和 q, 完整的flow就已经确定
Parameters
----------
image: h, w, c
p : n*2, (x, y)
q : n*2, (x, y)
Returns
-------
return flow:p->q, shape like image, h*w*2: (x, y)
'''
eps = 1e-8
height, width = image.shape[:2]
gridX = np.arange(width, dtype=np.int16)
gridY = np.arange(height, dtype=np.int16)
xx, yy = np.meshgrid(gridX, gridY)
n = len(p)
q = q.astype(np.float32).reshape(n, 1, 1, 2)
p = p.astype(np.float32).reshape(n, 1, 1, 2)
v = np.dstack((xx, yy))
w = 1.0 / (np.sum((p - v) ** 2, axis=-1) + eps) ** 1
w_norm = w / np.sum(w, axis=0, keepdims=True)
p_star = np.sum(p * w_norm.reshape(-1, height, width, 1), axis=0) # 1, h, w, 2
q_star = np.sum(q * w_norm.reshape(-1, height, width, 1), axis=0) # 1, h, w, 2
p_hat = p - p_star # n, h, w, 2
q_hat = q - q_star # n, h, w, 2
#print(p_hat.shape, q_hat.shape, w_norm.shape)
A_1row = np.sum(p_hat[..., 0][..., None] * p_hat * w_norm[..., None], axis=0) # 1, h, w, 2
A_2row = np.sum(p_hat[..., 1][..., None] * p_hat * w_norm[..., None], axis=0) # 1, h, w, 2
b_1row = np.sum(p_hat[..., 0][..., None] * q_hat * w_norm[..., None], axis=0) # 1, h, w, 2
b_2row = np.sum(p_hat[..., 1][..., None] * q_hat * w_norm[..., None], axis=0) # 1, h, w, 2
A = np.dstack((A_1row, A_2row)).reshape(height, width, 2, 2)
b = np.dstack((b_1row, b_2row)).reshape(height, width, 2, 2)
#print(A.shape, b.shape, A[:1, :1, :, :])
# a11 = A[..., 0, 0]
# a12 = A[..., 0, 1]
# a21 = A[..., 1, 0]
# a22 = A[..., 1, 1]
# A_det = a11 * a22 - a12 * a21
# A_inv = np.dstack((a22, -a12, -a21, a11)) / A_det[..., None]
# A_inv = A_inv.reshape(height, width, 2, 2)
A_inv = np.linalg.inv(A)
M = np.einsum("ijmk,ijkn->ijmn", A_inv, b)
x = v.reshape(height, width, 1, 2) - p_star.reshape(height, width, 1, 2)
y = np.einsum("ijmk,ijkn->ijmn", x, M) + q_star.reshape(height, width, 1, 2)
flow = y.reshape(height, width, 2) - v
#print(flow.shape, flow.dtype)
return flow
3.3 方法三
使用molesq python lib(https://github.com/clbarnes/molesq)
tran = Transformer(p, q)
xx, yy = np.meshgrid(np.arange(w), np.arange(h))
input = np.dstack((xx, yy)).reshape(-1, 2).astype(np.float32)
deformed = tran.transform(input)
input = input.reshape(h, w, 2)
deformed = deformed.reshape(h, w, 2)
flow = deformed - input
flow = flow.astype(np.float32)
3.4 实验结果
if __name__ == "__main__":
p = np.array([
[155, 30], [155, 125], [155, 225],
[235, 100], [235, 160], [295, 85], [293, 180.0]
])
q = np.array([
[211.0, 42], [155, 125], [100, 235],
[235, 80], [235, 140], [295, 85], [295, 180]
])
# 转化为 (x, y) format
p = p[..., ::-1]
q = q[..., ::-1]
file = r"images/toy.jpg"
img = cv2.imread(file, 1)[..., ::-1]
################################################### start
# p = np.array([[1, 1], [3, 0], [3, 1], [3, 2]]) # x,y
# q = np.array([[0, 1], [4, 5], [4, 6], [4, 7]]) # 0.5
# p = np.array([[1, 1], [3, 1], [3, 1.1], [3, 0.9]]) # x,y
# q = np.array([[0, 1], [4, 1], [4, 1.1], [4, 0.9]]) # 0.5
# show_fig = 0
# img = img[:10, :10, :]
################################################ end
img1 = img.copy()
h, w, c = img.shape
print(h, w, c)
flow = cal_affine_flow(img, p, q, 1)
print(' flow 1:\n', np.round(flow[..., 0], 2))
# print(' flow 1:', np.round(flow[100:110, 100:110, 1], 2))
img_warp1 = flow_warp(img, img, flow)
show_fig= 1
if show_fig:
show_flow_im(img, flow)
plt.figure()
plt.imshow( img_warp1)
plt.show()
flow = mls_affine_my(img, p, q)
img_warp2 = flow_warp(img, img, flow)
# print(' flow 2:', np.round(flow[100:110, 100:110, 1], 2))
print(' flow 2:\n', np.round(flow[..., 0], 2))
if show_fig:
show_flow_im(img, flow)
plt.figure()
plt.imshow(np.hstack((img, img_warp2)))
plt.show()
tran = Transformer(p, q)
xx, yy = np.meshgrid(np.arange(w), np.arange(h))
input = np.dstack((xx, yy)).reshape(-1, 2).astype(np.float32)
deformed = tran.transform(input)
input = input.reshape(h, w, 2)
deformed = deformed.reshape(h, w, 2)
flow = deformed - input
flow = flow.astype(np.float32)
img_warp3 = flow_warp(img1, img1, flow)
# print(' flow 3:', np.round(flow[100:110, 100:110, 1], 2))
print(' flow 3:\n', np.round(flow[..., 0], 2))
if show_fig:
show_flow_im(img1, flow)
plt.figure()
plt.imshow(np.hstack((img_warp1, img_warp2, img_warp3)))
plt.show()
结果如下:方法一 与 方法二,三的结果略有不同?

https://github.com/search?q=Moving+Least+Squares
4. 点的分布是否要求均匀?
当有一些点聚在一起,会产生大的影响,即使 偏移很小。?
因此点应该均匀?
不均匀好像也没影响:
曲线上面代码的注释:
################################################### start
# p = np.array([[1, 1], [3, 0], [3, 1], [3, 2]]) # x,y
# q = np.array([[0, 1], [4, 5], [4, 6], [4, 7]]) # 0.5
# p = np.array([[1, 1], [3, 1], [3, 1.1], [3, 0.9]]) # x,y
# q = np.array([[0, 1], [4, 1], [4, 1.1], [4, 0.9]]) # 0.5
# show_fig = 0
# img = img[:10, :10, :]
################################################ end
x 坐标由1 变为0, 从3变为4。
即使从3变为4的点比较多, x坐标为2的位置 的flow仍然是 0
5. 对于起始点固定的情况比较友好,可以提前计算出A
然后每次目标变化的时候A也是不变的。适用比如人脸识别场景, 人脸第一帧的特征点是固定不变的,其余帧的特征点变化,但是A是不变的, 不需要重复计算。
6. 代码优化(https://github.com/Jarvis73/Moving-Least-Squares)
clip 应该到 h-1, w-1更好,而不是设为0

其次结果不必取整,通过插值warp image。 修改后的代码在 本文 3.1 方法一
7. 关于weight 是否有更好的方式,来应对其他应用
目前mlq是根据点之间的距离计算weight
更好的weight计算方法,比如考虑图像内容差异。双边weight等。
8. 计算问题
求逆有问题的情况等需要考虑
9. 相关资料
最好阅读原文Image Deformation Using Moving Least Squares,其他一些blog也可以参考
https://blog.csdn.net/u011426016/article/details/125243631
https://blog.csdn.net/DIAJEY/article/details/114322764
https://github.com/Jarvis73/Moving-Least-Squares 中的PDF介绍的不错
10. 应用
可以用在曲面拟合上, 3Dlut拟合, 光流图,深度图拟合优化等
比如光流:
从光流图上随机选择300个point, 查看应用mlq插值后的结果
原图:

随机选取的点,以及预测的点:
蓝, 红 是 x方向的 ground truth和 predict
黄, 黑 是 x方向的 ground truth和 predict

预测的光流图:
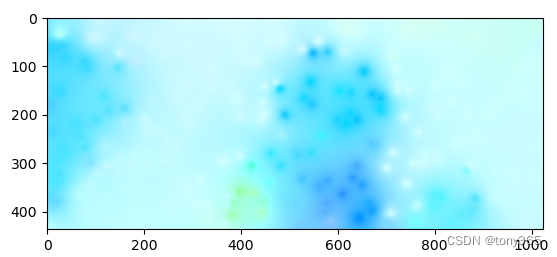
code如下:
def generate_flow():
def load_flow_to_numpy(path):
with open(path, 'rb') as f:
magic = np.fromfile(f, np.float32, count=1)
assert (202021.25 == magic), 'Magic number incorrect. Invalid .flo file'
w = np.fromfile(f, np.int32, count=1)[0]
h = np.fromfile(f, np.int32, count=1)[0]
data = np.fromfile(f, np.float32, count=2 * w * h)
data2D = np.reshape(data, (h, w, 2))
# print(data2D[:10,:10,0])
return data2D
file = r'C:\Users\rp\source\repos\dis_flow\dis_flow\frame_0001.flo'
flow_gt = load_flow_to_numpy(file)
return flow_gt
if __name__ == "__main__":
import os
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"
## 1. 载入光流图
flow_gt = generate_flow()
print(flow_gt.shape, flow_gt.dtype, flow_gt.min(), flow_gt.max())
flow_gt_im = flow_to_image_torch(flow_gt)
plt.figure()
plt.imshow(flow_gt_im)
plt.show()
# 2. 随机选择 N 对 match point
N = 300
h, w, c = flow_gt.shape
hh = np.arange(0, h)
ww = np.arange(0, w)
xx, yy = np.meshgrid(ww, hh)
tx = xx + flow_gt[..., 0]
ty = yy + flow_gt[..., 1]
pp = np.hstack((xx.reshape(-1, 1), yy.reshape(-1, 1)))
qq = np.hstack((tx.reshape(-1, 1), ty.reshape(-1, 1)))
# 3. 计算 光流
train_index = np.random.randint(0, len(pp), N)
p = pp[train_index]
q = qq[train_index]
flow = cal_affine_flow(flow_gt_im, p, q)
ret = np.dstack((xx, yy)) - flow
# 4. 画图
pic = 1
if pic:
# 画散点图
# 1. ground truth
fig = plt.figure()
ax1 = fig.gca(projection='3d')
ax1.scatter(p[..., 0], p[..., 1], q[..., 0]-p[..., 0], )
ax1.scatter(p[..., 0], p[..., 1], q[..., 1]-p[..., 1], )
# 2. predict
z = ret.reshape(-1, 2)[train_index]
ax2 = fig.gca(projection='3d')
ax2.scatter(p[..., 0], p[..., 1], p[..., 0] - z[..., 0], marker='+', c='r')
ax2.scatter(p[..., 0], p[..., 1], p[..., 1] - z[..., 1], marker='+', c='k')
plt.show()
flow_im = flow_to_image_torch(flow.astype(np.float32))
plt.figure()
plt.imshow(flow_im)
plt.show()
11. 应用:生成optical flow 和 3Dlut

import os
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"
import cv2
import numpy as np
from molesq import Transformer
from tps import show_lut_2d
def cal_flow_from_points_mlq(image, p, q):
h, w = image.shape[:2]
tran = Transformer(p, q)
xx, yy = np.meshgrid(np.arange(w), np.arange(h))
input = np.dstack((xx, yy)).reshape(-1, 2).astype(np.float32)
deformed = tran.transform(input)
input = input.reshape(h, w, 2)
deformed = deformed.reshape(h, w, 2)
flow = deformed - input
flow = flow.astype(np.float32)
return flow
def lut_id(lut_dim = 17):
lut = []
# remember that CUBE LUT requires BGR indexing
bin = 1.000 / (lut_dim - 1)
for b in range(lut_dim):
for g in range(lut_dim):
for r in range(lut_dim):
lut.append([ r*bin, g*bin, b*bin ])
lut = np.array(lut).astype(np.float32)
return lut
def gen_3dlut_from_points_mlq(rgb1, rgb2, dim):
tran = Transformer(rgb1, rgb2)
p = lut_id(dim).reshape(-1, 3)
lut3d = tran.transform(p).reshape((dim, dim, dim, 3))
return lut3d
if __name__ == "__main__":
file1 = r'D:\code\3dlut\lut1.png'
file2 = r'D:\code\3dlut\lut2.png'
im1 = cv2.imread(file1)[..., ::-1] / 255
im2 = cv2.imread(file2)[..., ::-1] / 255
im1 = im1[::10, ::10, :]
im2 = im2[::10, ::10, :]
rgb1 = im1.reshape(-1, 3).astype(np.float32)
rgb2 = im2.reshape(-1, 3).astype(np.float32)
lut_dim = 17
lut3d = gen_3dlut_from_points_mlq(rgb1, rgb2, lut_dim)
show_lut_2d(lut3d, lut_dim)





























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








