PRML-系类二之2.1

二元变量

　　我们首先考虑一个二元随机变量x∈{0,1}。例如，x可以描述抛硬币的结果，其中x=1表示正面而x=0表示反面。我们可以想像，这是一个损坏的硬币，所以正面的概率并不一定等于反面的概率。x=1的概率由参数μ表示

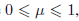
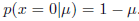
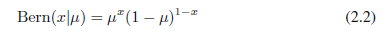
其中，由此得到。x上的概率分布可以写作:

这就是伯努利分布。很容易证实它是归一化的并且均值和方差为:

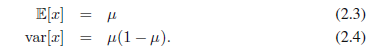
　　现在假设我们有观测值x的一个数据集D ={x1，，， xn}。我们可以构建似然函数，它是μ的函数，并且假设观测是从p（x|μ）中独立取出来的，从而：

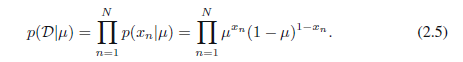
在频率论背景下，我们可以通过最大化似然函数来估计μ的值，或者等效地通过最大化对数似然。针对伯努利分布，对数似然函数由下式给出：

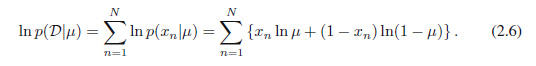
在这一点上，值得一提的是对数似然函数取决于N个观察值和的形式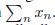。这个和提供了这个分布数据充分统计的例子，并且我们还将学习到充分统计量的一些细节。如果我们设置lnp（D|μ）关于μ的导数等于零，那么我们将得到最大似然估计：

它也被叫做样本均值。如果我们用m来表示样本集中x=1出现的数目，那么我们可以将(2.7)写成以下形式：

　　现在假设我们抛硬币，抛了3次并且都观测到正面向上。那么N = M= 3，μML=1。在这种情况下，最大似然结果将预测今后所有观测值将是正面向上。常识告诉我们这是不合理的，而实际上这是与最大似然那相关的过拟合的一个极端例子。我们将很快看到如何通过引进μ的先验分布得到更加明智的结论。
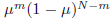
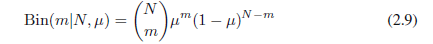
　　我们也可以计算出观测值x = 1数目的分布，鉴于该数据集的大小N。这就是所谓的二项式分布，并且从（2.5）我们看到，它正比于。为了获得归一化系数，我们注意到抛N个硬币，我们就必须添加m次正面朝上的所有可能方式，这样的话二项式分布可以写为：

其中
是从N个形同对象中选择m个对象的方式总数。图2.1展示了N = 10，μ = 0.25的二项式分布。
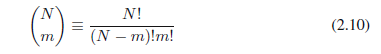
　　二项式分布的方差和方差通过使用练习1.10的结果可以找到，该结果表明，独立事件总和的均值就是均值的总和，并且总和的方差就是方差的总和。因为m = x1+，，， + xn，并且每个观测的均值和方差分别由（2.3）和（2.4）给出，所以我们有：

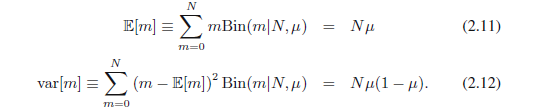
这些结果可以用微积分直接证明。

Beta分布

　　我们从（2.8）看到，最大似然（设置伯努利分布中的参数μ）根据数据集中x = 1的观察部分给定。正如我们已经注意到的，这可以对小的数据集产生严重的过拟合结果。为了开发一个这种问题的贝叶斯处理，我们需要引入参数μ的先验分布p（μ）。我们考虑先验分布的形式，它有一个简单的解释以及一些有用的分析属性。为了激励这个先验，我们注意到，似然函数采用各因素相乘的形式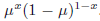。如果我们选择的先验正比于μ和（1-μ）的幂，那么后验分布（正比于先验和似然函数的乘积）将具有和先验相同的函数形式。这种性质称为共轭，我们稍后会看到它的几个例子。因此，我们选择先验（被称为Beta分布）由下式给出：

其中Γ（x）是由（1.141）定义的伽玛函数，（2.13）中的系数确保beta分布是归一化的，从而

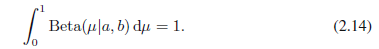
beta分布的均值和方差是：

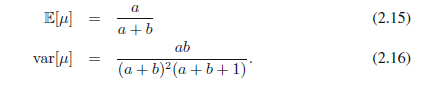
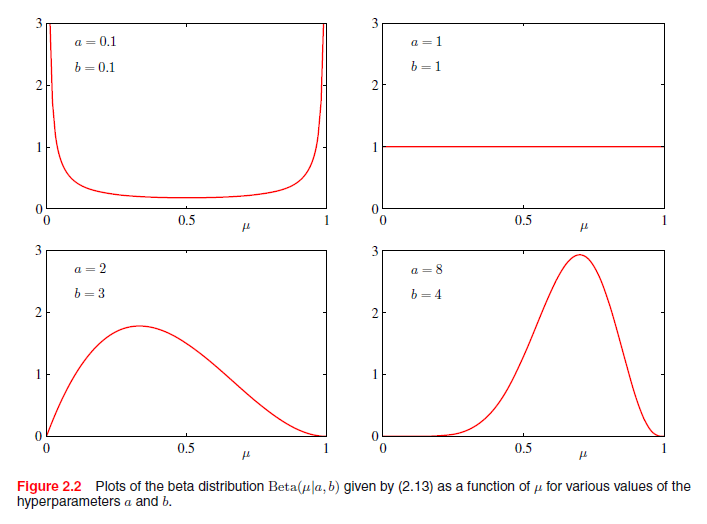
参数a和b通常被称为超参数，因为它们控制参数μ的分布。图2.2显示对于不同的超参数，Beta分布的曲线图

　　μ的后验分布现在通过将beta先验（2.13）和二项式似然函数（2.9）相乘并归一化获得。只保留依赖于μ的因子，我们看到，这个后验分布的形式：

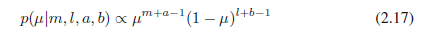
其中l= N- m，并且对应于硬币例子中反面的数量。我们看到，（2.17）对μ与先验有相同的函数依赖，反映了先验对于似然函数的共轭性质。事实上，这只是另一种简单的beta分布，其归一化系数通过比较（2.13）可以得到

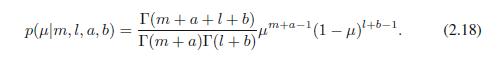
　　我们看到，观测数据集（x=1有m个观察值，x=0有l个观察值）的效果是a加上了m，b加上了l。基于此，我们可以解释先验中超参数a和b分别为x= 1和x = 0观测的有效数，注意a和b不必是整数。此外，如果我们随后观察额外的数据，后验分布可以充当先验。为了证明这一点，我们可以想象一次取一个观测值，之后乘以新观测值的似然函数来更新当前当前的后验分布，然后归一化获得新的修改后的后验分布。在每个阶段，后验是一个beta分布，x = 1和x = 0的观察值的数目由参数a和b给定。额外的x= 1观察值的参入仅仅对应于a的值加1，而对于x= 0的观察值，我们在b上增加1。 图2.3展示了这一步。

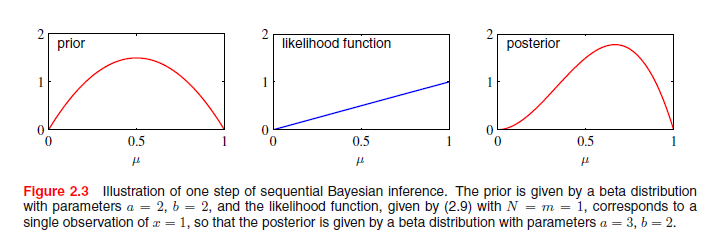
　　我们看到，当我们采用贝叶斯观点时，这个顺序的学习方式自然而然的产生了。先验和似然函数的选择是独立的，仅仅依赖于独立同分布数据的假设。连续的方法一次一个或小批次的使用观测值，然后在下一次观察被使用前舍弃他们。他们是有用的，例如，在实时的学习场景中，稳定的数据流将要到达时，必须在所有数据被看见之前作出预测。因为它们不需要整个数据集被存储或加载到存储器，顺序方法也可用于大型数据集。最大似然法也可铸造成顺序的框架。
　　如果我们的目标是预测接下来实验的结果，那么我们必须评估x的预测分布（观测数据集D已经给定）。根据概率的求和和乘积规则，它的形式为：

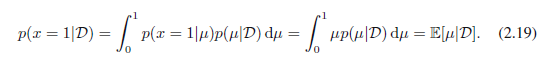
用后验分布p（μ|D）的结果（2.18）以及beta分布均值的结果（2.15），我们得到：

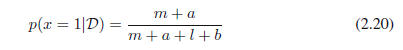
它简单的解释为对应于x=1的观测值（实际观测和虚构先验观测）总数。注意，在无穷大的数据集m中，l→∞，结果（2.20）降低到最大似然结果（2.8）。正如我们看到的，这是一个非常普遍的属性，即贝叶斯和最大似然结果在无限的条件下相同。
对于有限的数据集，μ的后验均值始终位于先验均值和μ（μ对应于（2.7）给出的相关事件频率）的最大似然估计之间。
从图2.2我们看到，随着观测值数量的增加，后验分布变得更加明显见顶。这也可以从beta分布的方差结果（2.16）看出来，其中我们看到方差在a→∞或b→∞时趋向于零。事实上，我们可能怀疑它是否是贝叶斯学习的一般属性，因为我们观察的数据越多，后验分布代表的不确定性将稳步下降。
　　为了解决这个问题，我们可以采取贝叶斯学习的频率论观点，表明（一般而言）的确持有这样的属性。考虑参数θ的一般贝叶斯推理问题，在该问题中我们观察到了数据集D，用联合分布p（θ，D）来描述。下面的结果：

其中

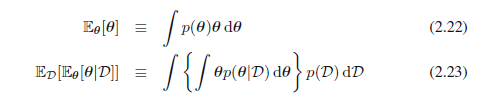
θ的后验均值等于θ的先验均值。同样，我们可以证明

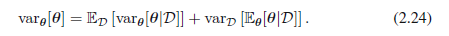
（2.24）左手侧是θ的先验方差。在右手侧中，第一项是θ的平均后验方差，第二项衡量θ后验均值的方差。因为这个方差是正值，所以这样的结果表明（一般来说）θ的后验方差小于先验方差。如果后验均值的方差较大的话，方差的减少也较大。然而，注意，这个结果仅限于一般情况，并且，对于一个特定的观测数据集，后验方差很可能大于先验方差。