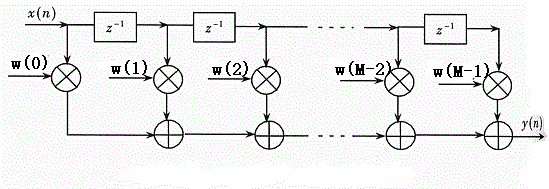
设输入序列为 x ( n ) x(n) x(n)，抽头系数为 ω ( m ) \omega(m) ω(m)，则输出序列可表示为
y ( n ) = ∑ m ω ( m ) x ( n − m Δ ) (1) y(n)=\sum_m \omega(m)x(n-m\Delta) \tag{1} y(n)=m∑ω(m)x(n−mΔ)(1)
其中， Δ \Delta Δ表示延迟单元。若 Δ = 1 \Delta=1 Δ=1，则表示图1中是以一个采样点为单位进行延迟的。若 Δ ≠ 1 \Delta \neq 1 Δ=1，则表示延迟单元不等于一个采样点，比如在FFE均衡器中，延迟单元通常为一个符号周期，此时 Δ \Delta Δ等于一个符号包含的采样点数。
设FIR滤波器的冲激响应为 h ( n ) h(n) h(n)，则滤波器输出
最低0.47元/天 解锁文章
扫一扫
1398
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
