图论 —— 竞赛图

最新推荐文章于 2024-02-06 19:22:54 发布

Alex_McAvoy

最新推荐文章于 2024-02-06 19:22:54 发布

阅读量1.6w

点赞数 4

分类专栏： ——————图论—————— # 图论——竞赛图

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/u011815404/article/details/100073600

版权

——————图论—————— 同时被 2 个专栏收录

23 篇文章

订阅专栏

图论——竞赛图

2 篇文章

订阅专栏

【概述】

竞赛图是一定义在有向图上的概念，图中每对不同的顶点通过单个有向边连接，即每对顶点间都有一条有向边。

设 D 为 n 阶有向简单图，若 D 的基图为 n 阶无向完全图，则 D 为 n 阶竞赛图。

简单来说，竞赛图就是将完全无向图的无向边给定了方向。

竞赛图有许多性质，比如在哈密顿问题中，对于 n 阶竞赛图，当 n 大于等于 2 时一定存在哈密顿通路，关于 n 阶竞赛图下构造有向图的哈密顿通路：点击这里

【兰道定理】

兰道定理（Landau’s Theorem）是用来判定竞赛图的定理。

将一个竞赛图的每一个点的出度从小到大排序后得到的序列称为竞赛图的比分序列

那么，兰道定理的内容为：

对于一个长度为 n 的序列 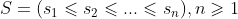$S=(s_1\leqslant s_2\leqslant...\leqslant s_n ),n\geqslant 1$ 是合法的比分序列，当且仅当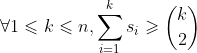： $\forall 1\leqslant k\leqslant n,\sum_{i=1}^k s_i\geqslant \binom{k}{2}$ ，且 k=n 时，式子必须要取等

关于兰道定理的证明：点击这里

【例题】

Football Games（HDU-5873）：点击这里

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。