智能优化算法：战争策略算法-附代码

最新推荐文章于 2025-02-24 12:22:24 发布

智能算法研学社（Jack旭）

最新推荐文章于 2025-02-24 12:22:24 发布

阅读量2.3k

点赞数

分类专栏：智能优化算法文章标签：算法机器学习数据挖掘

本文链接：https://blog.csdn.net/u011835903/article/details/126599876

版权

智能优化算法专栏收录该内容

154 篇文章

订阅专栏

智能优化算法：战争策略算法

摘要：WSO 是 Ayyarao 等人于 2022 年提出一种基于古代战争策略的新型元启发式优化算法。该算法灵感来自于古代战争中的攻击策略和防御策略，并通过士兵在战场上的位置更新来达到求解优化问题的目的。具有寻优能力强，收敛速度快的特点

1.战争策略算法

WSO 基于以下假设：①军队士兵随机分布于战场并攻击对方军队；攻击力最强的士兵为指挥官；国王是军队的最高领袖。②士兵根据国王和指挥官的位置动态更新位置。③国王根据战场上的局势通过战鼓动态地改变策略。④士兵根据附近士兵位置和国王位置来改变其位置。⑤对于战斗力最低的士兵或受伤的士兵，通过新兵替换或重新安置的策略进行位置更新。⑥所有士兵都有同等的概率成为国王或指挥官。

1.1 攻击策略

士兵根据国王和指挥官的位置来更新自己的位置。数学描述为
$X_i(t+1)=X_i(t)+2 \times \text { rand } \times(C-\text { King })+\operatorname{rand} \times\left(W_i \times \operatorname{King}-X_i(t)\right) \tag{1}$
式中, $X_i(t+1)$ 为第 $t + 1$ 次迭代士兵新位置; $X_i(t)$ 为第 $t$ 次迭代士兵位置; $C$ 为指挥官位置; King 为国王位置; rand 为介于 0 和 1 之间的随机数; $W_i$ 为国王位置的权重。

1.2 排序和权重。

士兵的等级 $R_i$ 取决于他在战场上的攻击力 (适应度值)。若士兵新位置的攻击力 $F_n$ 小于前代位置的攻击力 $F_p$ , 则士兵占据前一个位置。数学描述为
$X_i(t+1)=\left(X_i(t+1)\right) \times\left(F_n \geqslant F_p\right)+\left(X_i(t)\right) \times\left(F_n<F_p\right) \tag{2}$
若士兵成功更新位置, 则士兵等级 $R_i$ 将得到提升。数学描述为
$R_i=\left(R_i+1\right) \times\left(F_n \geqslant F_p\right)+\left(R_i\right) \times\left(F_n<F_p\right) \tag{3}$
根据士兵的攻击力 (适应度值) 进行排序, 权重更新数学描述为:
$W_i=W_i \times\left(1-R_i / T\right)^\alpha \tag{4}$
式中, $F_n$ 为士兵新位置攻击力 (适应度值); $F_p$ 为士兵前代位置攻击力 (适应度值); $R_i$ 为第 $i$ 个士兵的等级; $\alpha$ 为指数变化因子。

1.3防御策略

士兵根据附近士兵位置和国王位置来改变其位置, 并在不输掉战斗的情况下最大限度地保护国王。数学描述为
$X_i(t+1)=X_i(t)+2 \times \text { rand } \times\left(\text { King }-X_{\text {rand }}(t)\right)+\operatorname{rand} \times W_i \times\left(C-X_i(t)\right) \tag{5}$
式中, $X_{\text {rand }}(t)$ 为第 $t$ 次迭代士兵的随机位置; 其他参数意义同上。

1.4替换或安置弱兵。

WSO 利用两种方式更新弱兵位置: 一是利用式 (6) 中给出的随机士兵位置替换弱兵位置; 二是通过式 (7）将弱兵安置到更靠近整个战场中位数的位置, 这将有利于提高算法的收敛性。

$X_w(t+1)=L b+\operatorname{rand} \times(U b-L b) \tag{6}$

$X_w(t+1)=-(1-\operatorname{randn}) \times\left(X_w(t)-\operatorname{median}(X)\right)+K i n g\tag{7}$

式中, $X_w(t+1)$ 为第 $t + 1$ 次迭代替换或安置的弱兵位置; $U b 、 L b$ 为搜索空间的上、下限值; $X_w(t)$ 为第 $t$ 次迭代弱兵位置; randn 为 0 和 1 之间均匀分布的随机数; median (.) 为中位数函数。
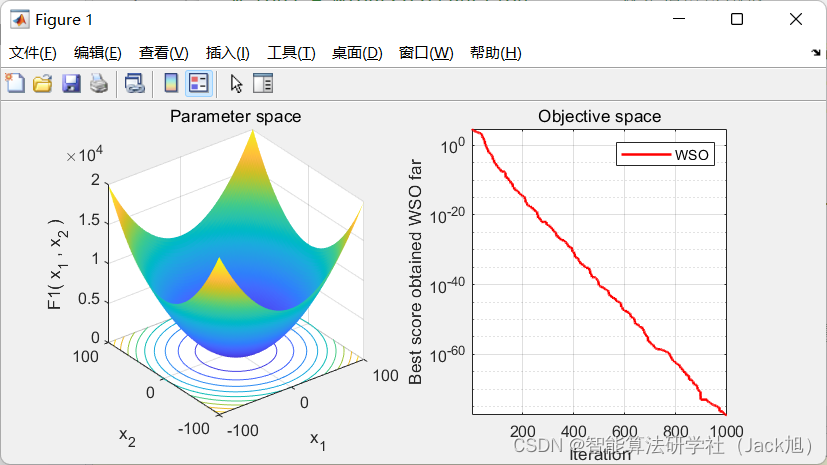
请添加图片描述

3.实验结果

请添加图片描述

4.参考文献

[1] T. S. L. V. Ayyarao et al., “War Strategy Optimization Algorithm: A New Effective Metaheuristic Algorithm for Global Optimization,” in IEEE Access, vol. 10, pp. 25073-25105, 2022, doi: 10.1109/ACCESS.2022.3153493.