2048游戏回顾二：算法总结（移动、合并、动画等）

如果只是单纯的写一个2048游戏，让这个游戏可以玩的话，工作量还是蛮小的。不过，在这写工作中，你可能花时间最多的就是数字的移动与合并的算法了，如果没有做过，可能确实要花点时间来构思，所以，写完2048游戏以后，我希望能把它做个记录。

移动与合并的算法

比如说我们有如下一个界面：

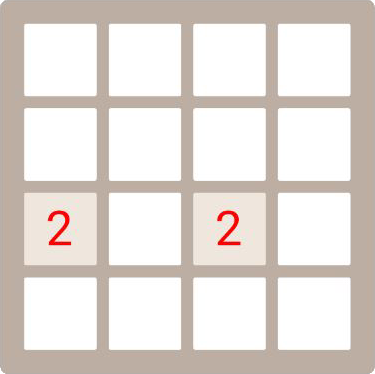
现在，玩家向左划，这个导致所有的数字向左移动，并且移动的过程中如果发生碰撞，会检查数字是不是可以合并。
我们的算法应该是通用的，不仅对于4*4模式，即便是针对3*3模式，n*n模式，它都应该是一样的。
那么怎么做呢？其实就两步：
第一步：把第一个空格和空格后面的第一个数字（如果有）交换。
第二步：交换后检查需不需要合并。
以此类推。
为了便于陈述，我们给图片做一个坐标：

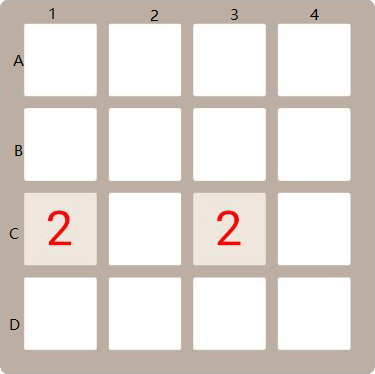
在这张图片中，按照我们说的，第一个空白和第一个数字交换，也就是把（2，C）和（3，C）交换，交换后检查能不能合并，如果能则合并，不过不能则不合并，这里显然可以合并，所以我们把他们合并为4.然后空白后面就没有数字了，算法结束。
因此，我们的算法必须记录第一个空白的位置和第一个数字的位置，那么我们用k记录空白，用j记录第一个数字，然后对于每一行，从左向右做这样的事情。
直接上代码吧，结合代码一说就会明白：
首先，我们的一个数字使用一个Number类来表述：

public class Number {
   
    public int mScores;
    public int mCurPosition;
    public int mBeforePosition;
    public boolean isNeedMove;
    public boolean isNeedCombine;
    public Number(int position,int scores){
        mScores = scores;
        mCurPosition = mBeforePosition = position;
        isNeedMove = false;
        isNeedCombine = false;
    }
    public void reset(){
        mScores = 0;
        isNeedMove = false;
        isNeedCombine = false;
    }
}

可见一个Number中有scores，也就是分数，当前的位置和之前的位置是用来计算动画的，我们需要把一个Number从之前的位置移动到当前的位置。
然后整个游戏使用一个Numbers类来表述：

public class Numbers {
    Number [][] mNumbers = new Number[Game2048StaticControl.gamePlayMode][Game2048StaticControl.gamePlayMode];
    public Numbers(){
        for(int i=0;i<Game2048StaticControl.gamePlayMode;i++){
            for(int j=0;j<Game2048StaticControl.gamePlayMode;j++){
                mNumbers[i][j] = new Number(0,0);
            }
        }
    }
    public Number getNumber(int x,int y){
        return mNumbers[x][y];
    }
    public Number [][] getNumbers (){
        return mNumbers;
    }
    public int getBlankCount(){
        int count = 0;
        for(int i=0;i<Game2048StaticControl.gamePlayMode;i++){
            for(int j=0;j<Game2048StaticControl.gamePlayMode;j++){
                if(mNumbers[i][j].mScores==0){
                    count++;
                }
            }
        }
        return count;
    }
    public int getPositonFromBlankCountTh(int blankTh){
        int count = 0;
        for(int i=0;i<Game2048StaticControl.gamePlayMode;i++){
            for(int j=0;j<Game2048StaticControl.gamePlayMode;j++){
                if(mNumbers[i][j].mScores==0){
                    if(count==blankTh){
                        return i*Game2048StaticControl.gamePlayMode+j;
                    }else {
                        count++;
                    }
                }
            }
        }
        return -1;
    }
    public void swapNumber(int position1,int position2){
        mNumbers[position1/Game2048StaticControl.gamePlayMode][position1%Game2048StaticControl.gamePlayMode].mCurPosition = position2;
        mNumbers[position1/Game2048StaticControl.gamePlayMode][position1%Game2048StaticControl.gamePlayMode].mBeforePosition = position1;
        mNumbers[position2/Game2048StaticControl.gamePlayMode][position2%Game2048StaticControl.gamePlayMode].mCurPosition = position1;
        mNumbers[position2/Game2048StaticControl.gamePlayMode][position2%Game2048StaticControl.gamePlayMode].mBeforePosition = position2;
        Number tem = mNumbers[position1/Game2048StaticControl.gamePlayMode][position1%Game2048StaticControl.gamePlayMode];
        mNumbers[position1/Game2048StaticControl.gamePlayMode][position1%Game2048StaticControl.gamePlayMode] = mNumbers[position2/Game2048StaticControl.gamePlayMode][position2%Game2048StaticControl.gamePlayMode];
        mNumbers[position2/Game2048StaticControl.gamePlayMode][position2%Game2048StaticControl.gamePlayMode] = tem;
    }
}

这个类的核心就是一个Number [n][n]的数组，n可以为任意值，因为我们的算法是通用的。

有了这个的概念以后，我们来看向左移动的算法，思想前面已经讲过了，直接看代码，结合代码非常容易理解。

   //return 0:do nothing
    //return 1:move
    //return 2:combine
    public int