笔者最近正在做四旋翼惯性导航的部分,利用加速度计进行速度估计、位置估计,从而实现四旋翼的垂直方向上的定高、水平方向上的定点控制。
首先在这里引用学长之前参考APM飞控里面互补滤波惯导融合方案:原文见四旋翼位置控制之-定高篇
原文将四轴在悬停油门附近的高度控制,等效为对光滑地面上滑块的位置、速度、加速度模型的控制。
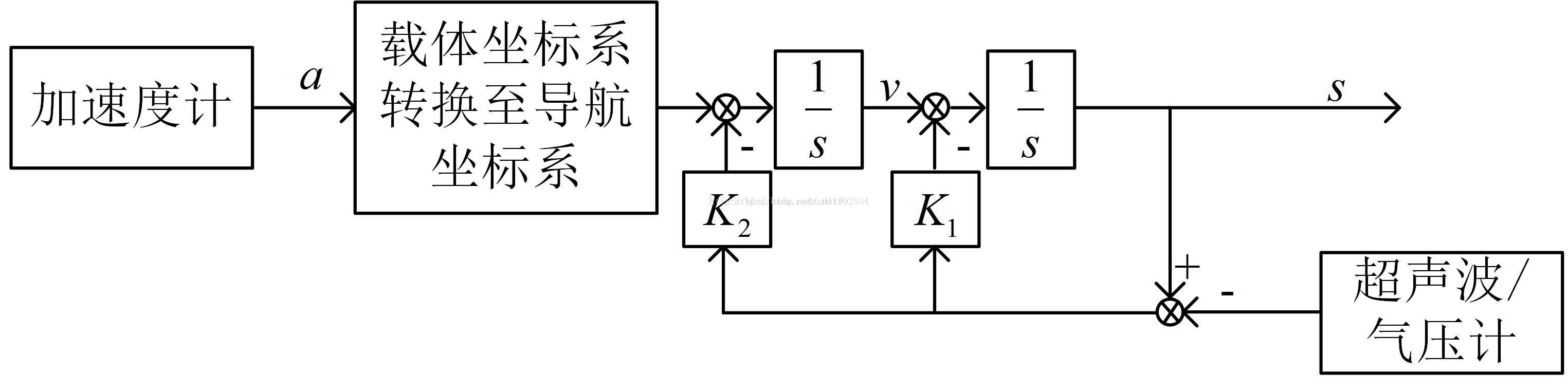
下图为王龙学长博客里面的融合框图:
首先将载体坐标系下的加速度(记作A(b)=(ax,ay,az)^T)旋转到导航坐标系上下,导航坐标系下的加速度记为A(n)=(AX,AY,AZ)^T,这里A(b),A(n)均为列向量,其中T表示转置。
有:A(n)=A(b)*R(b2n)
其中R(b2n)表示载体坐标系到导航系的旋转矩阵,下面是方向余弦矩阵的推导
/*Z-Y-X顺规欧拉角转方向余弦矩阵
//Pitch Roll Yaw 分别对应Φ θ Ψ
X轴旋转矩阵
R(Φ)
{1 0 0 }
{0 cosΦ sinΦ}
{0 -sinΦ cosΦ }
Y轴旋转矩阵
R(θ)
{cosθ 0 -sinθ}
{0 1 0 }
{sinθ 0 cosθ}
Z轴旋转矩阵
R(θ)
{cosΨ sinΨ 0}
{-sinΨ cosΨ 0}
{0 0 1 }
由Z-Y-X顺规有:
载体坐标系到导航坐标系下旋转矩阵R(b2n)
R(b2n) =R(Ψ)^T*R(θ)^T*R(Φ)^T
R(b2n)=
{cosΨ*cosθ -cosΦ*sinΨ+sinΦ*sinθ*cosΨ sinΨ*sinΦ+cosΦ*sinθ*cosΨ}
{cosθ*sinΨ cosΦ*cosΨ +sinΦ*sinθ*sinΨ -cosΨ*sinΦ+cosΦ*sinθ*sinΨ}
{-sinθ cosθsin Φ cosθcosΦ }
在计算R(b2n)的过程中也可以采用四元数旋转矩阵来实现,避免进行大量的三角函数运算,这里直接截取论文里面的图片如下。
根据上述公式可得导航坐标系下加速度A(n)为:
A(n)_X=Cos_Yaw* Cos_Roll * A(b)_X
+(Sin_Pitch*Sin_Roll*Cos_Yaw-Cos_Pitch * Sin_Yaw) * A(b)_Y
+(Sin_Pitch * Sin_Yaw+Cos_Pitch * Sin_Roll * Cos_Yaw) * A(b)_Z;
A(n)_Y=Sin_Yaw* Cos_Roll * A(b)_X
+(Sin_Pitch * Sin_Roll * Sin_Yaw +Cos_Pitch * Cos_Yaw) * A(b)_Y
+ (Cos_Pitch * Sin_Roll * Sin_Yaw - Sin_Pitch * Cos_Yaw) * A(b)_Z;
A(n)_Z=-Sin_Roll* A(b)_X
+ Sin_Pitch *Cos_Roll * A(b)_Y
+ Cos_Pitch * Cos_Roll *A(b)_Z;
由此我们得到了导航系下的加速度量,这里需要注意的是此时我们得到的加速度量并不全是用于惯性导航的运动加速度,因为加速度计为比力模型,所有作用在加速度计上的惯性力都将对其产生比力加速度。在载体坐标系中,重力(0,0,1)g始终作用在加速度计上。
对于时间非常短的导航 ,当忽略地球自转和哥氏项所引起的 误差的情况下有:
所以为得到到用于导航的运动加速度Acce(x,y,z)转化为cm/s^2有:
Acce(x)*=9.8/AcceMax;
Acce(x)*=100;//加速度cm/s^2
Acce(y)*=9.8/AcceMax;
Acce(y)*=100;//加速度cm/s^2
Acce(z)*=9.8/AcceMax;
Acce(z)-=9.8;
Acce(z)*=100;//加速度cm/s^2
至此我们得到了三组用于导航的运动加速度量,这里注意一点的是,水平运动加速度Acce(x),Acce(y)在这里表示的是四旋翼沿着正北(纬度)、正东(经度)运动的加速度。AcceMax为加度素计1G量程下的值。
下面贴出本文参考APM三阶互补位置融合的代码:
#define TIME_CONTANST_Z5.0f
#define K_ACC_Z (5.0f / (TIME_CONTANST_Z * TIME_CONTANST_Z * TIME_CONTANST_Z))
#define K_VEL_Z (3.0f / (TIME_CONTANST_Z * TIME_CONTANST_Z))
#define K_POS_Z (3.0f / TIME_CONTANST_Z)
float High_Filter[3]={
0.03,//0.015
0.05,//0.05
0.02//0.03
};
float Altitude_Dealt=0;
void Strapdown_INS_High()
{
//Altitude_Dealt=HC_SR04_Distance-NamelessQuad.Position[_YAW];//气压计(超声波)与SINS估计量的差,单位cm
Altitude_Dealt=Altitude_Estimate-NamelessQuad.Position[_YAW];//气压计(超声波)与SINS估计量的差,单位cm
acc_correction[_YAW] += High_Filter[0]*Altitude_Dealt* K_ACC_Z ;//加速度校正量
vel_correction[_YAW] += High_Filter[1]*Altitude_Dealt* K_VEL_Z ;//速度校正量
pos_correction[_YAW] += High_Filter[2]*Altitude_Dealt* K_POS_Z ;//位置校正量
//原始加速度+加速度校正量=融合后的加速度
NamelessQuad.Acceleration[_YAW]=Origion_NamelessQuad.Acceleration[_YAW]+acc_correction[_YAW];
//融合后的加速度积分得到速度增量
SpeedDealt[_YAW]=NamelessQuad.Acceleration[_YAW]*CNTLCYCLE;
//得到速度增量后,更新原始位置
Origion_NamelessQuad.Position[_YAW]+=(NamelessQuad.Speed[_YAW]+0.5*SpeedDealt[_YAW])*CNTLCYCLE;
//原始位置+位置校正量=融合后位置
NamelessQuad.Position[_YAW]=Origion_NamelessQuad.Position[_YAW]+pos_correction[_YAW];
//原始速度+速度校正量=融合后的速度
Origion_NamelessQuad.Speed[_YAW]+=SpeedDealt[_YAW];
NamelessQuad.Speed[_YAW]=Origion_NamelessQuad.Speed[_YAW]+vel_correction[_YAW];
}
作者在去年寒假的之前基本上都是用的上述方案进行气压计定高融合,效果还比较好,实际融合调试过程中,只需要调整三个积分系数即可,如果你之前的位置观测量是采用气压计,当你直接把高度位置观测量换成超声波时,参数基本不用调整,融合就挺好的。
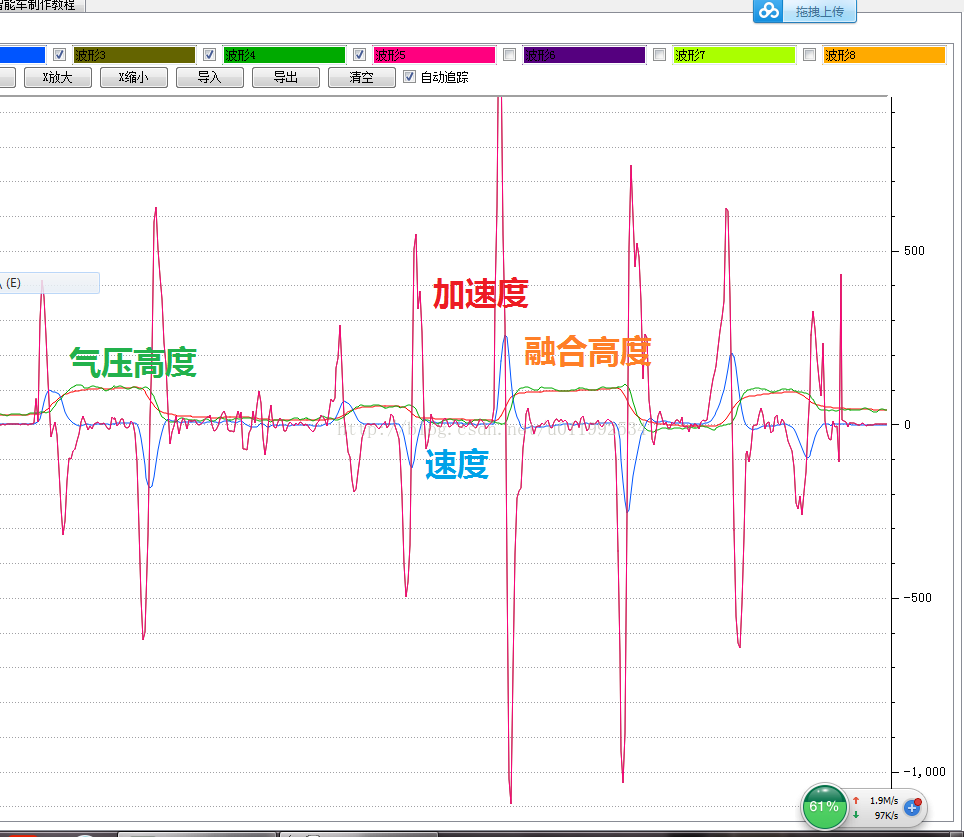
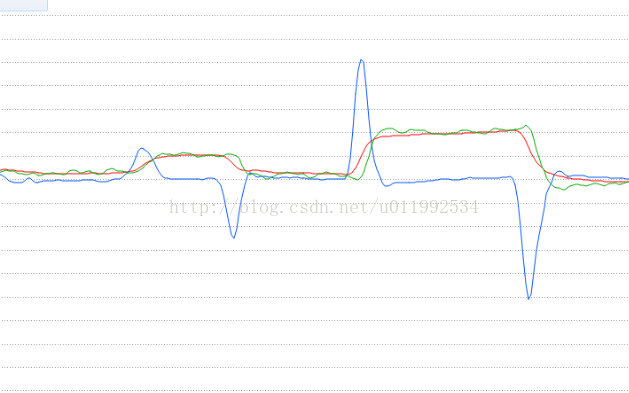
下面给出之前测试时候融合波形:
三阶互补融合方案,在飞机中、低速的上升或者下降的时候,不
处理延时修正时,由于观测传感器带来的滞后感不明显,但是当
你快速拖动飞机,你会发现位置融合波形在后半段会出现跟踪缓
慢,强行被观测传感器拉至稳定值的情况,这里截取一小段融合
波形给大家,大家对比一下速度快和慢的时候位置融合就一目了
然了。
问题先留在这里,如何处理这样一类因观测传感器滞后的造成的惯导融合滞后的问题?
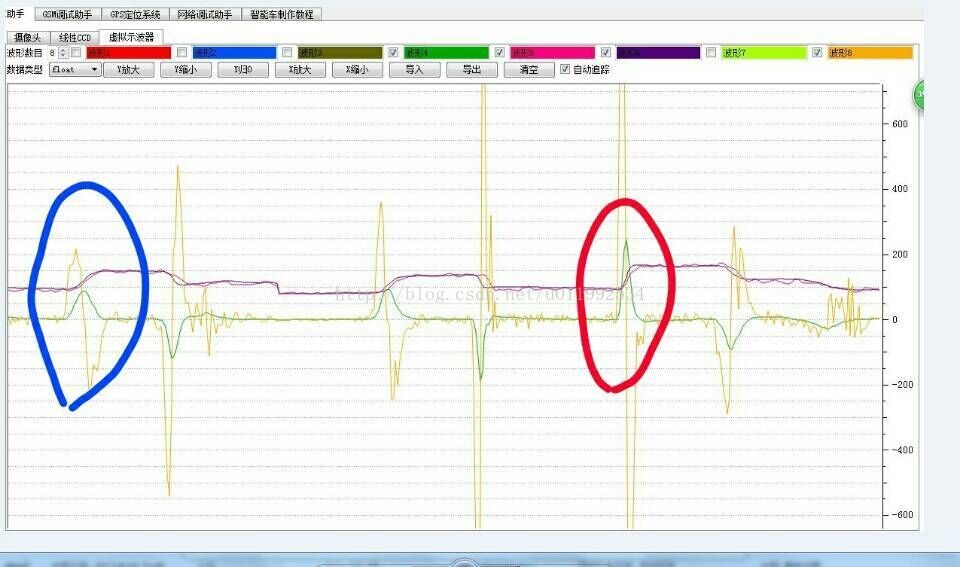
贴上处理后的融合波形,大家仔细对比下:
附上之前寒假的三阶互补室外定高视频:
视频1:室外定高F330机架
视频2:QAV250穿越机
以上内容,均为作者学习四轴的个人总结与
感悟,难免有错误之处,欢迎批评指出,谢
谢!!!
作者将在下一节阐述观测传感器延时修正的
处理,以及基于GPS速度+位置两个观测量
的水平位置卡尔曼融合过程。








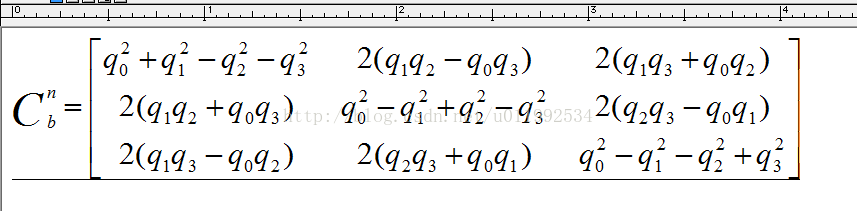
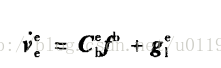














 317
317

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








