论文阅读：The Perfect Match

原创已于 2022-10-12 14:06:21 修改

· 1k 阅读

5 ·

版权

文章标签：

#论文阅读 #深度学习 #计算机视觉

于 2020-03-20 12:21:45 首次发布

论文阅读笔记专栏收录该内容

7 篇文章

订阅专栏

提出一种紧凑型学习局部特征描述子，用于3D点云匹配，创新点包括SDV体素化输入表示和全卷积暹罗网络结构，实现高效、旋转不变的3D特征描述。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

论文阅读：The Perfect Match

The Perfect Match: 3D Point Cloud Matching with Smoothed Densities

1、现存问题

大场景三维重建需要将不同视角捕获的具有低重叠区域的点云拼接在一起。现有的点云配准方法有基于几何约束的，有匹配对应3D特征描述符的（如点分布直方图和局部表面法向量），有随着深度学习回归二研究3D局部特征的，这些学习的3D特征描述符要么不具备旋转不变性，要么需要非常高的输出维度才能成功，或者很难适应新的领域（这个地方我看到他引用的是两篇17年的文章，后续看看为啥不能适应新领域）

2、创新点

1、提出了一种针对3D点云匹配的紧凑学习局部特征的描述子
2、SDV体素化是一种新的服务于全卷积层的输入数据的表示方式
3、SDV可以一方面降低了输入体素网格的密度，使反向传播中的梯度流动更好同时降低了边界损失和由于局部参考系估计中的误差而造成的误差。另一方面，我们假设它明确地对深度网络通常在第一层学习的平滑进行建模，从而节省了学习高度描述性特征的网络容量。其次，我们提出了一个具有全卷积层的暹罗网络结构，它学习了一个非常紧凑、旋转不变性的3D局部特征描述子。
4、他们的输出只有16或者32个维度，这样加速了对应区域的搜索，使实时成为可能

3、内容

文章先描述了一下现有的两大类点云特征：手工3D局部描述子和基于学习的3D局部描述子。指出从原始点云直接训练网络实现了端到端学习范式，但是也阻碍了卷积层的作用。因此，文章采用了一种混合策略，首先，将点邻域转换成LRFs，其次，将未构造的三维点云编码为能够适应对流层的SDV网格，第三，使用siamese CNN学习描述性特征。
文章的流程步骤为
（1）给定两个原始点云
（2）随机选择的兴趣点的球形邻域的LRF
（3）将邻域转换为统一的表示
（4）借助高斯平滑体素化他们
（5）利用3DSmoothNET推断每个点的局部特征并作为基于随机样本一致性的鲁棒点云配准管道的输入

3.1、输入参数化

估计点云的局部参考系

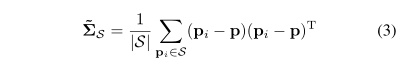
在这里插入图片描述
其中 $\{ {p_i}:||{p_i} - p|{|_2} \le {r_{LRF}}\}$ , ${r_{LRF}}$ 代表用于估计LRF的邻域半径（这里提到了一篇PR的文章只用了1/3的半径，原因未明，并且强调了自己是用兴趣点p替代邻域中心）
接着文章选择z轴 $\mathop {{z_p}}\limits^ \wedge$ 作为共线估计作为最小特征矩阵 $\sum\limits_{}^ \sim S$ 特征向量的法向量 $\mathop {{n_p}}\limits^ \wedge$ ，文章通过公式（4）计算 $\mathop {{z_p}}\limits^ \wedge$
在这里插入图片描述
x轴的 $\mathop {{x_p}}\limits^ \wedge$ 被计算作为权重向量的和

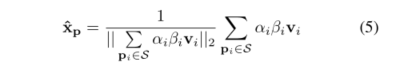
其中 ${v_i} = \overrightarrow {p{p_i}} - \left\langle {\overrightarrow {p{p_i}} ,} \right.\left. {{{\widehat z}_p}} \right\rangle {\widehat z_p}$ 是向量 $\overrightarrow {p{p_i}}$ 在正交于 $\mathop {{z_p}}\limits^ \wedge$ 的面上的投影，其中 ${\alpha _i}$ 和 ${\beta _i}$ 是权重值
在这里插入图片描述
直观来说 ${\alpha _i}$ 更喜欢靠近兴趣点的点，这样让 $\mathop {{x_p}}\limits^ \wedge$ 应对簇和遮挡更鲁棒， ${\beta _i}$ 对大规模投影给予更多的权重（尤其在平面区域，这里还是PR那篇文章里有讲述）最终 $\mathop {{y_p}}\limits^ \wedge$ 被根据左手定则计算 ${\widehat y_p} = {\widehat x_p} \times {\widehat z_p}$

平滑密度值体素化

一旦在局部坐标系S中的点 ${p_i} \in S$ 被变换为统一的表示 ${p_i}' \in S'$ ，文章用这些点来表示转换后的兴趣点的局部邻域。文章用SDV体素化网格表示以兴趣点 $p^{'}$ 为中心并且用LRF对齐后的点。将SDV体素化网格用三维矩阵 ${X^{SDV}} \in {R^{W \times H \times D}}$ 表示，其中元素 ${({X^{SDV}})_{jkl}} = :{x_{jkl}}$ 表示用带带宽h的高斯平滑核计算的响应体素的SDV
在这里插入图片描述
其中 ${n_{jkl}}$ 代表 ${p_i}' \in S'$ 距离体素中心 ${c_{jkl}}$ $3 h$ 范围内的点数量。此外，所有X SDV的值都被归一化，使它们之和为1，以实现相对于可变点云密度的不变性。
为什么要用体素化表示呢，因为：
1、通过对体素上的密度值进行平滑处理，减轻了二进制占用网格和截断距离函数的边界效应和噪声的影响。
2、想必也二进制展位网格降低了稀疏性使得反向传播的梯度流动的更好。
3、SDV代表有助于我们的方法实现更好的泛化，因为我们没有在训练中过度拟合准确的数据线索。
4、与手工制作的特征表示不同，SDV体素网格表示为输入提供了几何形式的结构，这能够利用卷积层，这对捕获点云的局部几何特征的至关重要。