7.1点和斑点 419
7.1.1特征检测器 422
7.1.2特征描述符 434
7.1.3特征匹配 441
7.1.4大规模匹配和检索 448
7.1.5特征跟踪 452
7.1.6应用:性能驱动动画 454
7.2边缘和轮廓 455
7.2.1边缘检测 456
7.2.2轮廓检测 461
7.2.3应用:边缘编辑和增强 465
7.3剖面跟踪 466
7.3.1蛇与剪刀 467
7.3.2水平集 474
7.3.3应用:轮廓跟踪和转描 476
7.4线与消失点 477
7.4.1连续逼近 477
7.4.2 Hough变换 477
7.4.3消失点 481
7.5分段 483
7.5.1基于图的分割 486
7.5.2平均偏移 487
7.5.3标准化切割 489
7.6其他阅读材料 491
7.7练习 495

图7.1特征检测器和描述子可用于分析、描述和匹配图像:(a)点状兴趣算子(Brown,Szeliski和Winder 2005)©2005 IEEE;(b) GLOH描述子(Mikolajczyk和Schmid 2005);(c)边缘(Elder和Goldberg 2001)©2001 IEEE;(d)直线(Sinha,Steedly等2008)©2008 ACM;(e)图基合并(Felzenszwalb和Huttenlocher 2004)©2004 Springer;(f)均值漂移(Comaniciu和Meer 2002)©2002 IEEE。
特征检测与匹配是许多计算机视觉应用中的关键组成部分。考虑图7.2中展示的两组图像。对于第一组,我们可能希望将两张图像对齐,以便无缝拼接成一个复合马赛克(第8.2节)。对于第二组,我们可能希望建立一组密集的对应关系,以便构建3D模型或生成中间视图(第12章)。无论哪种情况,你应该检测并匹配哪些类型的特征来建立这种对齐或对应关系?在继续阅读之前,请花点时间思考这个问题。
你可能首先注意到的是图像中的特定位置,如山峰、建筑角落、门道或形状有趣的雪地。这些局部特征通常被称为关键点特征或兴趣点(甚至角点),通常通过该位置周围像素块的外观来描述(第7.1节)。另一类重要的特征是边缘,例如山峦与天空的轮廓(第7.2节)。这类特征可以根据其方向和局部外观(边缘轮廓)进行匹配,也是图像序列中物体边界和遮挡事件的良好指标。边缘可以组合成长曲线和环线,然后进行跟踪(第7.3节)。它们也可以组合成直线段,可以直接匹配或分析以找到消失点,从而确定内部和外部相机参数(第7.4节)。
在本章中,我们描述了一些检测这些特征的实际方法,并讨论了如何在不同图像之间建立特征对应关系。点特征现在被广泛应用于各种场景,因此阅读并实现第7.1节中的一些算法是很好的做法。边缘和线条提供了与关键点和基于区域的描述符互补的信息,非常适合描述制造物体的边界。这些替代描述符虽然非常有用,但在简短的入门课程中可以跳过。
本章的最后一部分(第7.5节)讨论了自下而上的非语义分割技术。尽管这些技术曾广泛用作识别和匹配算法的重要组成部分,但它们大多已被我们在第6.4节中研究的语义分割技术所取代。这些技术偶尔仍被用于将像素聚类在一起,以实现更快或更可靠的匹配。
点特征可用于在不同图像中找到一组稀疏的对应位置,通常作为计算相机姿态(第11章)的前体,而计算相机姿态是使用立体匹配(第12章)计算更密集对应位置的前提条件。

图7.2两对要匹配的图像。可以使用哪些特征来建立这些图像之间的对应关系?
对应点还可以用于对齐不同的图像,例如,在拼接图像马赛克(第8.2节)或高动态范围图像(第10.2节),以及执行视频稳定(第9.2.1节)。它们还广泛用于对象实例识别(第6.1节)。关键点的一个重要优势是,即使在存在遮挡(如被遮挡)和大规模及方向变化的情况下,也能进行匹配。
基于特征的对应技术自立体匹配早期就已使用(Hannah1974;Moravec1983;Hannah1988),随后在图像拼接应用中(Zoghlami、Faugeras和Deriche1997;Brown和Lowe 2007)以及全自动三维建模中(Beardsley、Torr和Zisserman1996;Schaf-falitzky和Zisserman2002;Brown和Lowe2005;Snavely、Seitz和Szeliski2006)也获得了广泛的应用。
寻找特征点及其对应关系主要有两种方法。第一种是在一张图像中找到可以使用局部搜索技术(如相关性或最小二乘法)准确跟踪的特征点(第7.1.5节)。第二种是独立检测所有待考虑图像中的特征点,然后根据它们的局部外观进行匹配(第7.1.3节)。前者更适合于从附近视角拍摄或快速连续拍摄的图像(例如视频序列),而后者则更适合于预期会有大量运动或外观变化的情况,例如拼接全景图(Brown和Lowe 2007年)、在宽基线立体中建立对应关系(Schaffalitzky和Zisserman 2002年)或执行物体识别。

图7.3图片对,提取的补丁如下。注意一些补丁可以比其他补丁更精确地定位或匹配。
(Fergus,Perona和Zisserman2007)。
在本节中,我们将关键点检测和匹配流程分为四个独立阶段。在特征检测(提取)阶段(Section7.1.1),每张图像都会搜索出可能与其他图像良好匹配的位置。在特征描述阶段(第7.1.2节),每个检测到的关键点周围区域会被转换成一个更紧凑且稳定的(不变的)描述符,以便与其他描述符进行匹配。特征匹配阶段(Sections7.1.3and 7.1.4)高效地搜索其他图像中可能的匹配候选。特征跟踪阶段(Section7.1.5)是第三阶段的替代方案,仅搜索每个检测到特征的小邻域,因此更适合视频处理。
一个很好的例子可以在大卫·洛(2004)的论文中找到,该论文描述了他尺度不变特征变换(SIFT)的发展和完善过程。关于替代技术的全面描述可以在一系列综述和评估论文中找到,这些论文涵盖了特征检测(施密德、莫尔和鲍克哈格2000;米科拉伊奇克、图特拉尔斯等人2005;图特拉尔斯和米科拉伊奇克2008)和特征描述子(米科拉伊奇克和施密德2005;巴尔纳斯、伦斯等人2020)。石和托马西(1994)以及特里格斯(2004)也提供了经典(神经网络前)特征检测的良好综述。

图7.4不同图像区域的孔径问题:(a)稳定(“角状”)流动;(b)经典孔径问题(梳状幻象);(c)无纹理区域。两幅图像I0(黄色)和I1(红色)叠加在一起。红色向量u表示区域中心之间的位移,w(xi)加权函数(区域窗口)以深色圆圈显示。
7.1.1特征检测器
我们如何找到可以与其他图像可靠对应的位置,即哪些是好的特征来跟踪(Shi和Tomasi 1994;Triggs 2004)?再次查看图7.3中显示的图像对和三个样本补丁,看看它们匹配或跟踪的效果如何。你可能会注意到,无纹理的补丁几乎无法定位。具有大对比度变化(梯度)的补丁更容易定位,尽管单一方向上的直线段会受到孔径问题的影响(Horn和Schunck 1981;Lucas和Kanade 1981;Anandan 1989),也就是说,只能沿边缘方向的法线方向对齐补丁(图7.4b)。至少在两个(显著)不同方向上有梯度的补丁最容易定位,如图7.4a所示。
这些直觉可以通过查看比较两个图像块的最简单的匹配标准来形式化,即它们的(加权)平方差之和,
其中,I0和I1是要比较的两幅图像,u =(u,v)是位移向量,w(x)是空间变化的加权(或窗口)函数,求和i涵盖了补丁中的所有像素。请注意,这与我们后来用于估计完整图像之间运动的公式相同(第9.1节)。
在执行特征检测时,我们不知道该特征最终会与哪些其他图像位置匹配。因此,我们只能通过将图像块与之对比,来计算这一指标相对于位置△u的小变化的稳定性。

图7.5三个自相关表面EAC(Δu)以灰度图像和表面图的形式显示:(a)原始图像用三个红色十字标记,表示计算自相关表面的位置;(b)这个区域来自花坛(良好的唯一
最小);(c)这个斑块来自屋顶边缘(一维孔径问题);(d)这个斑块来自云层(没有好的峰值)。图b-d中的每个网格点都是Δu的一个值。
(图7.5)。1注意纹理花坛的自相关表面(图7.5b和图7.5a右下角的红色十字)表现出强烈的最小值,表明它可以很好地定位。屋顶边缘对应的关联表面(图7.5c)在一个方向上具有强烈的模糊性,而云区对应的关联表面(图7.5d)则没有稳定的最小值。
利用图像函数的泰勒级数展开,我们可以将自相关面近似为I0(xi+△u)≈I0(xi)+▽I0(xi)·△u(Lucas和Kanade1981;Shi和Tomasi1994),
(7.5)
= △uTA△u, (7.6)
在哪里
(7.7)
是图像在xi处的梯度。该梯度可以通过多种技术计算(Schmid,Mohr和Bauckhage 2000)。经典的“哈里斯”检测器(Harris和Stephens 1988)使用[–2–1 0 1 2]滤波器,但更现代的变体(Schmid,Mohr和Bauckhage 2000;Triggs 2004)则用高斯函数的水平和垂直导数对图像进行卷积(通常σ = 1)。
A = w *
我们用权重核w的离散卷积替换了加权求和。这个矩阵可以解释为一个张量(多带)图像,其中梯度▽I的外积与权重函数w卷积,以提供每个像素
自相关函数的局部(二次)形状估计。
1严格来说,相关性是两个补丁的乘积(3.12);我在这里使用这个术语是更定性的。加权平方差之和通常被称为SSD表面(第9.1节)。

正如Anandan(1984;1989)首次指出,并在Section9.1.3and方程(9.37)中进一步讨论,矩阵A的逆提供了匹配区域位置不确定性的下限。因此,它是判断哪些区域可以可靠匹配的有效指标。最直观地理解和分析这种不确定性的方法是对自相关矩阵A进行特征值分析,这会产生两个特征值(λ0;λ 1)和两个特征向量方向(图7.6)。由于较大的不确定性依赖于较小的特征值,即λ0-1/2,因此找到较小特征值的最大值来定位要跟踪的良好特征是有意义的(Shi和Tomasi 1994)。
弗斯特纳
-哈里斯。虽然阿南丹(1984)和卢卡斯与卡纳德(1981)是最早分析自相关矩阵不确定性结构的人,但他们是在将确定性与光流测量关联的背景下进行的。弗斯特纳(1986)和哈里斯与斯蒂芬斯(1988)首次提出使用从自相关矩阵
导出的旋转不变标量度量中的局部最大值来定位关键点,以实现稀疏特征匹配。这两种技术还建议使用高斯加权窗口代替之前使用的正方形块,这使得检测器响应对平面内图像旋转不敏感。
最小特征值λ0(Shi和Tomasi1994)不是唯一可以计算的量
用于寻找关键点。Harris和Stephens(1988)提出的一个更简单的量是
det(A)—Q轨迹(A)2=λ0λ1—Q(λ0 + λ1)2 (7.9)
与Q = 0.06不同,这个量不需要使用平方根,但仍然具有旋转不变性,并且还降低了边缘特征的权重
Schmid、Mohr和Bauckhage(2000)以及Triggs(2004)对特征检测算法进行了更详细的历史回顾。

图7.7流行的关键点检测函数的等值线(Brown、Szeliski和Winder 2004)。每个检测器都寻找特征值λ0,λ1均为较大的点。
λ1≥λ0. Triggs(2004)建议使用该数量
λ0 — Qλ 1 (7.10)
(例如,当Q=0.05时),这也会减少一维边缘处的响应,在这些位置上,混叠误差有时会放大较小的特征值。他还展示了如何将基本的2×2赫斯矩阵扩展到参数运动中,以检测在尺度和旋转方面也能准确定位的点。另一方面,布朗、泽利斯基和温德(2005)使用了调和平均值
(7.11)
在λ0≈λ1的区域内,这是一个更平滑的函数。图7.7显示了各种兴趣点算子的等值线,从中我们可以看到两个特征值是如何混合以确定最终的兴趣值的。图7.8展示了经典哈里斯检测器以及下面讨论的高斯差分(DoG)检测器的结果兴趣点响应。
自适应非极大值抑制(ANMS)。大多数特征检测器仅寻找兴趣函数中的局部最大值,这可能导致图像中特征点分布不均,例如,在高对比度区域特征点会更密集。为了缓解这一问题,Brown、Szeliski和Winder(2005)仅检测那些既是局部最大值且其响应值显著(10%)高于其半径r内所有邻居的特征点(图7.9c-d)。他们设计了一种有效的方法,通过首先按响应强度对所有局部最大值进行排序,然后创建

图7.8兴趣点运算器响应:(a)样本图像,(b) Harris响应,以及(c) DoG响应。圆圈的大小和颜色表示每个兴趣点检测的尺度。注意两个检测器往往在互补的位置响应。

图7.9自适应非极大值抑制(ANMS)(Brown,Szeliski和Winder 2005)©2005 IEEE:上两幅图像显示了最强的250个和500个兴趣点,而下两幅图像则展示了通过自适应非极大值抑制选择的兴趣点及其对应的抑制半径r。请注意,后者在图像中的空间分布更加均匀。

图7.10在五个金字塔层次上提取的多尺度定向补丁(MOPS)(Brown、Szeliski和Winder 2005)©2005 IEEE。方框显示了特征的方向和描述符向量采样的区域。
第二列表按抑制半径递减排序(Brown,Szeliski和Winder 2005)。图7.9展示了选择前n个特征与使用ANMS的定性比较。请注意,非极大值抑制现在也是基于DNN的目标检测器的重要组成部分,如第6.3.3节所述。
测量重复性。鉴于计算机视觉中已开发出大量特征检测器,我们如何决定使用哪些?Schmid、Mohr和Bauckhage(2000)首次提出了测量特征检测器的重复性,他们将其定义为在一个图像中检测到的关键点在变换后图像中相应位置∈(例如,∈= 1.5)像素内的出现频率。在他们的论文中,他们通过应用旋转、尺度变化、光照变化、视角变化以及添加噪声来转换平面图像。他们还测量了每个检测到的特征点可用的信息量,定义为一组旋转不变局部灰度描述符的熵。在他们调查的技术中,发现改进版(高斯导数)的Harris操作符,其中σd=1(导数高斯的尺度)和σi=2(积分高斯的尺度),效果最佳。
尺度不变性
在许多情况下,检测尽可能精细的稳定尺度特征可能不合适。例如,在匹配具有少量高频细节的图像(如云)时,
细粒度特征可能不存在。
解决这一问题的一个方法是在不同尺度上提取特征,例如,在金字塔结构中以多种分辨率执行相同操作,然后在相同层级匹配特征。当待匹配的图像没有发生大规模变化时,这种方法尤为适用,比如从飞机上连续拍摄的航拍图像或使用固定焦距相机拍摄的全景图拼接。图7.10展示了这种方法的一个输出:布朗、斯泽利斯基和温德(2005)提出的多尺度定向块检测器,显示了五个不同尺度下的响应。
然而,对于大多数物体识别应用而言,图像中物体的尺度是未知的。与其在多个尺度上提取特征,然后匹配所有这些特征,不如提取在位置和尺度上都稳定的特征(Lowe 2004;Mikolajczyk和Schmid 2004)。
早期关于尺度选择的研究由林德伯格(1993;1998b)进行,他首次提出使用高斯拉普拉斯(LoG)函数的极值作为兴趣点位置。基于这项工作,洛(2004)提出了计算一组次八度高斯差分滤波器(图7.11a),寻找结果结构中的三维(空间+尺度)最大值(图7.11b),然后使用二次拟合计算亚像素空间+尺度位置(布朗和洛2002)。经过仔细的经验调查,确定次八度级别的数量为三个,这对应于四分之一八度金字塔,与特里格斯(2004)使用的相同。
与Harris算子一样,对于指示函数(在这种情况下,是DoG)的局部曲率存在强烈不对称性的像素被拒绝。这是通过首先计算差异图像D的局部Hessian实现的
(7.12)
然后拒绝那些关键点

图7.11使用次八度高斯金字塔差分(Lowe2004)检测尺度空间特征©2004斯普林格:(a)相邻的次八度高斯金字塔层级相减,生成高斯差分图像;通过将像素与其26个邻近像素进行比较,检测出结果三维体积中的(b)极值(最大值和最小值)。
或小于其粗略和精细级别的值)。还提出了并评估了对尺度和位置的可选迭代优化。米科拉伊奇克、图特拉尔斯等人(2005)和图特拉尔斯与米科拉伊奇克(2008)讨论了其他尺度不变区域检测器的例子。
旋转不变性和方向估计
除了处理尺度变化外,大多数图像匹配和物体识别算法还需要应对(至少)平面内的图像旋转。一种解决方法是设计旋转不变的描述子(Schmid和Mohr 1997),但这些描述子的区分能力较差,即它们会将外观不同的区域映射到相同的描述子上。
更好的方法是估计每个检测到的关键点的主导方向。一旦估计了关键点的局部方向和尺度,就可以提取出一个围绕检测点的缩放和定向的补丁,并用于形成特征描述符(图7.10和7.15)。
最简单的方向估计是关键点周围区域内的平均梯度。如果使用高斯加权函数(Brown、Szeliski和Winder2005),

图7.12通过创建所有梯度方向的直方图(按其大小加权或在阈值化小梯度后)并找到该分布中的显著峰值,可以计算出主导方向估计值(Lowe2004)©2004 Springer。
这个平均梯度相当于一阶可调滤波器(第3.2.3节),即可以使用高斯滤波器的水平和垂直导数进行图像卷积来计算(Freeman和Adelson 1991)。为了使这一估计更加可靠,通常建议使用比检测窗口更大的聚合窗口(高斯核大小)(Brown、Szeliski和Winder 2005)。图7.10中所示的方框方向是通过这种方法计算得出的。
然而,有时一个区域内的平均(带符号)梯度可能很小,因此作为方向的指标不可靠。更可靠的方法是查看围绕关键点计算的方向直方图。Lowe(2004)计算了一个由边缘方向组成的36个区间直方图,该直方图根据梯度大小和到中心的高斯距离加权,并找到全局最大值80%范围内的所有峰值,然后使用三个区间的抛物线拟合计算出更准确的方向估计(图7.12)。
仿射不变性
虽然尺度不变性和旋转不变性非常理想,但对于许多应用,如宽基线立体匹配(Pritchett和Zisserman1998;Schaffalitzky以及Zisserman 2002)或位置识别(Chum、Philbin等2007),完全仿射不变性更为优选。仿射不变检测器不仅在尺度和方向变化后能在一致的位置响应,还能在仿射变形如(局部)透视缩短(图7.13)中保持一致的响应。事实上,对于足够小的图像块,任何连续的图像扭曲都可以很好地近似为仿射变形。
为了引入仿射不变性,一些作者提出了拟合椭圆到自动-

图7.13用于匹配从截然不同的视角拍摄的两幅图像的仿射区域探测器(Mikolajczyk和Schmid2004)©2004 Springer。

图7.14从多幅图像中提取并匹配的最大稳定极限区域(MSERs)(Matas,Chum et al.2004)©2004 Elsevier。
相关性或Hessian矩阵(使用特征值分析),然后使用该拟合的主要轴和比率作为仿射坐标系(Lindeberg和G rding1997;Baumberg 2000;Mikolajczyk
和Schmid2004;Mikolajczyk、Tuytelaars等2005;Tuytelaars和Mikolajczyk2008)。
另一个重要的仿射不变区域检测器是由马塔斯、楚姆等人(2004年)开发的最大稳定极值区域(MSER)检测器。为了检测MSERs,通过在所有可能的灰度级别上对图像进行阈值处理来计算二值化区域(因此该技术仅适用于灰度图像)。这一操作可以通过首先按灰度值对所有像素进行排序,然后随着阈值的变化逐步向每个连通组件中添加像素来高效完成(Nist r和Stew nius2008)。随着阈值的变化,监测每个组件(区域)的面积;那些相对于阈值面积变化率最小的区域被定义
为最大稳定的。因此,这些区域对仿射几何和光度(线性偏置增益或平滑单调)变换具有不变性(Figure7.14)。如有需要,可以使用其矩矩阵将每个检测到的区域拟合到一个仿射坐标系。
特征点检测领域依然非常活跃,每年在主要的计算机视觉会议上都会发表论文。Mikolajczyk、Tuytelaars等人(2005)和Tuytelaars和Mikolajczyk(2008)综述了多个流行的(DNN之前)仿射区域检测器,并提供了它们对常见图像变换不变性的实验比较。
最近十年发表的论文包括:
SURF (Bay,Ess等人,2008),使用积分图像进行更快的卷积;
•FAST和FASTER(Rosten、Porter和Drummond2010),最早的学会检测器之一;
•BRISK(Leutenegger、Chli和Siegwart2011),它使用尺度空间FAST检测器和位串描述符;
ORB (Rublee、Rabaud等人,2011年),为FAST添加了方向性;以及
KAZE (Alcantarilla、Bartoli和Davison,2012)和Accelerated-KAZE (Alcantarilla、Nuevo和Bartoli,2013),使用非线性扩散来选择特征的尺度
察觉
虽然FAST引入了机器学习用于特征检测器的想法,但最近的论文使用卷积神经网络来执行检测。这些包括:
学习协变特征检测器(Lenc和Vedaldi2016);
学习为特征点分配方向(Yi,Verdie等人,2016);
•LIFT,学习不变特征变换(Yi,Trulls等,2016),SuperPoint,自监督兴趣点检测与描述(DeTone,Malisiewicz和Rabi- novich,2018),以及LF-Net,从图像中学习局部特征(Ono,Trulls等,2018),这三种方法共同优化了检测器和描述符。
(多头)管道;
AffNet(Mishkin、Radenovic和Matas2018),用于检测可匹配的仿射协变区域;
Key.Net (Barroso-Laguna,Riba等人,2019),它使用手工制作和学习的CNN特征的组合;
D2-Net (Dusmanu、Rocco等人,2019)、R2D2 (Revaud、Weinzapfel等人,2019)和D2D (Tian、Balntas等人,2020),均提取密集的局部特征描述符
然后保留那些具有高显著性或可重复性的数据。
最后两篇论文也包含了对其他最近特征检测器的很好的回顾,Balntas、Lenc等人(2020)的论文也是如此。
当然,关键点并不是唯一可用于图像配准的特征。佐格拉米、福热拉斯和德里奇(1997)使用线段以及点状特征来估计图像对之间的单应性,而巴托利、科克雷尔和斯特姆(2004)则利用沿边缘的局部对应关系提取三维结构和运动。图特拉尔斯和范古尔(2004)使用仿射不变区域检测宽基线立体匹配中的对应关系,而卡迪尔、齐瑟曼和布雷迪(2004)则检测局部最大化的显著区域,这些区域的块熵及其随尺度变化的速率达到最大值。科索和哈格(2005)使用相关技术将二维定向高斯核拟合到同质区域。关于寻找和匹配曲线、直线和区域的技术的更多细节将在本章后面部分介绍。
检测到关键点特征后,我们必须进行匹配,即确定不同图像中相应位置的特征。在某些情况下,例如视频序列(Shi和Tomasi 1994)或已校正的立体对(Zhang、Deriche等1995;Loop和Zhang 1999;Scharstein和Szeliski 2002),每个特征点周围的局部运动可能主要是平移。在这种情况下,可以使用简单的误差度量,如平方差之和或归一化互相关,这些方法在第9.1节中有所描述,用于直接比较每个特征点周围小区域的强度。(Mikolajczyk和Schmid(2005)的研究,下文讨论,使用了互相关。)由于特征点可能无法精确定位,可以通过执行增量运动精化来计算更准确的匹配分数,如第9.1.3节所述,但这可能会耗时较长,有时甚至会降低性能(Brown、Szeliski和Winder 2005)。
然而,在大多数情况下,特征的局部外观会改变方向和尺度,有时甚至会发生仿射变形。因此,通常更倾向于提取局部尺度、方向或仿射框架估计值,然后使用这些信息重新采样补丁,再形成特征描述符(图7.15)。
即使补偿了这些变化,图像块的局部外观通常仍会因图像而异。我们如何使图像描述符对这种变化更加不变,同时仍能保持不同(非对应)图像块之间的可区分性?Mikolajczyk和Schmid(2005)回顾了多种视图不变的局部图像描述符,并实验比较了它们的性能。最近,Balntas、Lenc等人(2020)和Jin、Mishkin等人(2021)比较了过去十年开发的大量学习特征描述符。下面,我们将介绍其中的一些描述符。
3最近的许多出版物,如Tian,Yu等人(2019)使用他们的HPatches数据集来比较他们的性能

图7.15一旦确定了局部尺度和方向估计,就会使用偏置和增益归一化的强度值的8×8采样来形成MOPS描述符,采样间距为检测尺度的五像素(Brown,Szeliski,和Winder 2005)©2005 IEEE。这种低频采样使特征对兴趣点位置误差具有一定的鲁棒性,是通过在高于检测尺度的金字塔层级进行采样实现的。
更多细节。
偏置和增益归一化(MOPS)。对于不表现出大量前景缩短的任务,如图像拼接,简单的归一化强度块表现良好且易于实现(Brown,Szeliski和Winder 2005)(Figure7.15)。为了补偿特征点检测器(位置、方向和尺度)的轻微不准确,多尺度定向块(MOPS)以相对于检测尺度的五像素间距采样,使用图像金字塔的较粗层次以避免混叠。为了补偿仿射光度变化(线性曝光变化或偏置和增益,(3.3)),块强度被重新缩放,使其均值为零,方差为一。
尺度不变特征变换(SIFT)。SIFT特征(Lowe2004)是通过计算检测到的关键点周围16×16窗口中每个像素的梯度形成的,使用的是检测到关键点时所对应的高斯金字塔层级。梯度幅度通过高斯衰减函数(图7.16a中以蓝色圆圈表示)进行下权重处理,以减少远离中心的梯度的影响,因为这些梯度更容易受到小失配的影响。
在每个4×4象限中,通过(概念上)将梯度值乘以高斯衰减函数后加到八个方向直方图的一个区间内,形成梯度方向直方图。为了减少位置和主要方向估计错误的影响,每个原始的256个加权梯度幅度被柔和地添加到2×2×2相邻的区域。
与以前的方法相反。

图7.16洛(2004)尺度不变特征变换(SIFT)的示意图:(a)在每个像素处计算梯度的方向和强度,并通过高斯衰减函数加权(蓝色圆圈)。(b)然后在每个子区域中使用三线性插值计算加权梯度方向直方图。虽然此图显示了一个8×8像素的补丁和一个2×2的描述符数组,但洛的实际实现使用了16×16的补丁和一个4×4的八区间直方图数组。
使用三线性插值在(x;y;θ)空间中绘制直方图区间。在计算直方图的任何应用中,例如霍夫变换(第7.4.2节)或局部直方图均衡化(第3.1.4节),将值柔和地分配到相邻的直方图区间通常是个好主意。
四维数组中的八个区间直方图生成了128个非负值,构成了SIFT描述子向量的原始版本。为了减少对比度或增益的影响(梯度已经去除了加性变化),128维向量被归一化为单位长度。为进一步提高描述子对其他光度变化的鲁棒性,值被裁剪至0.2,然后再次归一化为单位长度。
PCA-SIFT。Ke和Sukthankar(2004)提出了一种更简单的计算描述子的方法,该方法受到SIFT的启发;它在39×39的补丁上计算x和y(梯度)导数,然后使用主成分分析(PCA)将结果的3042维向量降维至36维(第5.2.3节和附录A.1.2)。另一种流行的SIFT变体是SURF (Bay,Ess等2008),该方法使用盒滤波器来近似SIFT中使用的导数和积分。
RootsSIFT.Arandjelovi和Zisserman(2012
)观察到,通过使用L1度量重新归一化SIFT描述符,然后取每个分量的平方根,可以显著提高性能(可区分性)。

图7.17梯度位置-方向直方图(GLOH)描述符使用对数极坐标区间而不是正方形区间来计算方向直方图(Mikolajczyk和Schmid,2005)。GLOH在每个区间内使用16个梯度方向,尽管该图仅显示了8个以减少混乱。
梯度位置-方向直方图(GLOH)。这一描述符由米科拉伊奇克和施密德(2005)开发,是SIFT的一种变体,使用了对数极坐标分箱结构,而不是洛厄(2004)使用的四个象限(图7.17)。空间分箱范围为半径0.. .6、6.. .11和11.. .15,共有八个角度分箱(除了单个中心区域),总计17个空间分箱,而GLOH使用了16个方向分箱,而不是SIFT中的8个。然后,272维直方图通过在大型数据库上训练的主成分分析投影到128维描述符上。在他们的评估中,米科拉伊奇克和施密德(2005)发现,总体表现最佳的GLOH比SIFT略胜一筹。
可转向滤波器。可转向滤波器(第3.2.3节)是高斯滤波器的导数组合,允许快速计算所有可能方向上的偶数和奇数(对称和反对称)边缘特征和角特征(Freeman和Adelson1991)。由于它们使用了相当宽的高斯函数,因此对定位和方向误差也较为不敏感。
局部描述子的性能。在Mikolajczyk和Schmid(2005)比较的局部描述子中,他们发现GLOH表现最好,紧随其后的是SIFT。他们还给出了许多本书未涉及的其他描述子的结果。
特征描述子领域继续迅速发展,一些技术关注局部颜色信息(van de Weijer和Schmid 2006;Abdel-Hakim和Farag 2006)。Winder和Brown(2007)开发了一个多阶段框架,用于计算特征描述子,该框架涵盖了SIFT和GLOH(图7.18a),并且还允许它们

图7.18 SIFT、GLOH及一些相关特征描述子的空间求和块(Winder和Brown 2007)©2007 IEEE: (a)特征参数,例如高斯权重,是从互联网照片集合中应用鲁棒结构从运动得到的(b)匹配真实图像块训练数据库中学习而来的(Hua、Brown和Winder 2007)。
学习新的描述子以获得优于先前手动调优的描述子的最佳参数。Hua、Brown和Winder(2007)通过学习具有最佳区分能力的高维描述子的低维投影扩展了这一工作,而Brown、Hua和Winder(2011)进一步扩展了这项工作,学习池化区域的最佳放置。所有这些论文都使用了一个由真实世界图像补丁组成的数据库(图7.18b),这些图像是在互联网照片集合中使用稳健的结构从运动算法可靠匹配的位置采样的(Snavely、Seitz和Szeliski 2006;Goesele、Snavely等2007)。在同期研究中,Tola、Lepetit和Fua(2010)开发了一种类似的菊花描述子用于密集立体匹配,并根据真实立体数据优化了其参数。
虽然这些技术构建了优化所有对象类别重复性的特征检测器,但也有可能开发出针对特定类别或实例的特征检测器,以最大化与其他类别的区分度(Ferencz,Learned-Miller和Malik 2008)。如果可以在匹配图像中确定平面表面的方向,则还可以提取视角不变的补丁(Wu,Clipp等2008)。
最近的趋势是开发二进制位字符串特征描述子,这些描述子可以利用现代计算机架构中的快速汉明距离运算。简短描述子(Calonder,Lepetit等,2010)通过比较关键点周围散落的128对像素值(图7.19a中表示为线段)来获得一个128位向量。ORB (Rublee,Rabaud等,2011)在计算定向简短描述子之前,在fast检测器中添加了方向组件。BRISK(Leutenegger,Chli,和Siegwart,2011)在fast检测器中加入了尺度空间分析和径向对称采样模式(图7.19b),以生成二进制描述子。FREAK (Alahi,

图7.19二进制位串特征描述符:(a)简短的描述符比较了128对像素值(用线段表示),并将比较结果存储在一个128位向量中(Calonder,Lepetit等,2010)©2010 Springer;(b)快速采样模式和高斯模糊半径;(Leutenegger,Chli和Siegwart,2011)©2011 IEEE;(c) FREAK视网膜采样模式(Alahi,Ortiz和Vandergheynst,2012)©2012 IEEE。
Ortiz和Vandergheynst2012)使用了更明显的“视网膜”(对数极坐标)采样模式,并结合一系列位比较,以实现更高的速度和效率。Mukherjee、Wu和Wang(2015)的调查和评估比较了所有这些“经典”特征检测器和描述符。
自2015年以来,大多数新的特征描述符都是使用深度学习技术构建的,如Balntas、Lenc等人(2020)和Jin、Mishkin等人(2021)所调查的。其中一些描述符,例如LIFT(Yi、Trulls等人,2016)、TFeat(Balntas、Riba等人,2016)、HPatches (Balntas、Lenc等人,2020)、L2-Net (Tian、Fan、Wu,2017)、HardNet (Mishchuk、Mishkin等人,2017)、Geodesc (Luo、Shen等人,2018)、LF-Net (Ono、Trulls等人,2018)、SOSNet (Tian、Yu等人,2019)和Key.Net (Barroso-Laguna、Riba等人,2019),都是基于补丁操作的,类似于经典的SIFT方法。因此,它们需要一个初始的局部特征检测器来确定补丁的中心,并在构建网络输入时使用预设的补丁大小。
相比之下,诸如DELF (Noh,Araujo等,2017)、SuperPoint (DeTone,Malisiewicz和Rabinovich,2018)、D2-Net (Dusmanu,Rocco等,2019)、ContextDesc (Luo,Shen等,2019)、R2D2 (Revaud,Weinzaepfel等,2019)、ASLFeat(Luo,Zhou等,2020)和CAPS(Wang,Zhou等,2020)等方法使用整个图像作为描述子计算的输入。这还有一个额外的好处,即用于计算描述子的感受野可以从数据中学习,而不需要指定块大小。理论上,这些CNN模型可以学习到使用图像中所有像素的感受野,尽管在

图7.20 HPatches局部描述符基准测试(Balntas,Lenc等人,2020)©2019
IEEE:(a)特征描述符的年代学;(b)数据集中的典型补丁(按Easy、Hard和Tough分组);(c)不同描述符的大小和速度。
他们倾向于使用高斯样感受野(Zhou,Khosla等人,2015;Luo,Li等人,2016;Selvaraju,Cogswell等人,2017)。
在HPatches基准测试(图7.20)中,Balntas等人(2020)评估了补丁匹配,HardNet和L2-net平均表现最佳。另一篇论文(Wang,Zhou等人,2020)显示CAPS和R2D2表现最佳,而S2DNet (Germain,Bourmaud和Lepetit,2020)和LISRD (Pautrat,Larsson等人,2020)也声称达到了最先进水平,而WISW基准测试(Bellavia和Colombo,2020)则表明,传统的描述符如SIFT结合更近期的思想表现最好。在Jin,Mishkin等人(2021)的宽基线图像匹配基准测试中,HardNet、Key.Net和D2-Net是顶级表现者(例如,D2-Net具有最多的地标),尽管结果相当依赖于任务,高斯差异检测器仍然是最佳选择。这些描述符在大光照差异(昼夜)下匹配特征的表现也得到了研究(Radenovi,Sch nberger等人,2016;Zhou,Sattler和Jacobs,2016;Mishkin,2021)。最近在宽基线匹配领域的一个趋势是,在没有检测器阶段的情况下密集提取特征,然后匹配并优化对应关系集(江、特鲁尔斯等人2021;萨林、乌纳加尔等人2021;孙、沈等人2021;张、达内利扬等人2021;周、萨特勒和莱亚尔-泰克斯2021)。这些较新的技术中的一些已经
一旦我们从两张或多张图像中提取了特征及其描述符,下一步就是在这几张图像之间建立初步的特征匹配。我们采取的方法部分取决于应用,例如,对于已知重叠的图像(如图像拼接)与可能完全没有对应关系的图像(如尝试从数据库中识别对象时),不同的策略可能是更优的选择。
在本节中,我们将这个问题分为两个独立的部分。第一部分是选择匹配策略,这决定了哪些对应关系会被传递到下一阶段进行进一步处理。第二部分是设计高效的数据结构和算法,以尽可能快地完成这种匹配,相关内容将在第7.1.4节中详细展开。
匹配策略和错误率
确定哪些特征匹配是合理的进一步处理取决于匹配执行的上下文。假设我们有两张图像,它们有相当程度的重叠(例如,在图像拼接或视频中跟踪物体时)。我们知道一张图像中的大多数特征很可能与另一张图像匹配,尽管有些可能不匹配,因为它们被遮挡了或者外观变化太大。
另一方面,如果我们要识别一个杂乱场景中出现的已知物体数量(图6.2),大多数特征可能不匹配。此外,必须搜索大量潜在匹配的物体,这需要更有效的策略,如下所述。
首先,我们假设特征描述子已经设计得当,使得特征空间中的欧几里得(向量大小)距离可以直接用于潜在匹配的排序。如果发现某个描述子中的某些参数(轴)比其他参数更可靠,通常最好提前重新缩放这些轴,例如通过确定它们与其他已知良好匹配之间的差异(Hua,Brown,和Winder 2007)。一个更通用的过程是将特征向量转换到一个新的缩放基中,这被称为白化,在基于特征脸的人脸识别中会有更详细的讨论(第5.2.3节)。
给定欧几里得距离度量,最简单的匹配策略是设置一个阈值(最大距离),并返回该阈值范围内的所有其他图像的匹配结果。如果阈值设置过高,则会产生过多的假阳性,即返回错误的匹配结果。如果阈值设置过低,则会产生过多的假阴性,即错过太多正确的匹配结果(图7.21)。
我们可以通过以下方法量化匹配算法在特定阈值下的性能

图7.21假阳性和假阴性:黑色数字1和2是在与其他图像特征数据库匹配的特征。在当前阈值设置(实心圆圈)下,绿色1是真阳性(匹配成功),蓝色1是假阴性(未匹配),红色3是假阳性(匹配错误)。如果我们提高阈值(虚线圆圈),蓝色1会变成真阳性,但棕色4会成为额外的假阳性。

表7.1特征匹配算法正确估计和错误估计的匹配数量,显示了真正例(TP)、假正例(FP)、假反例(FN)和真反例(TN)的数量。各列之和等于实际的正例(P)和负例(N),而各行之和等于预测的正例(P9)和负例(N9)。文中给出了真正例率(TPR)、假正例率(FPR)、阳性预测值(PPV)和准确率(ACC)的计算公式。
首先计算正确和错误匹配以及匹配失败的数量,使用以下定义(Fawcett2006),我们在Section6.3.3中已经讨论过:
TP:真阳性,即正确匹配的数量;
FN:假阴性,未正确检测到的匹配;
FP:假阳性,错误的匹配建议;
TN:真阴性,正确拒绝的非匹配。
表7.1显示了包含此类数字的样本混淆矩阵(列联表)。
我们可以通过定义以下量将这些数字转换为单位率(Fawcett
真阳性率(TPR),
假阳性率(FPR),
阳性预测值(PPV),
准确度(ACC),
在信息检索(或文档检索)文献中(Baeza-Yates和Ribeiro-Neto 1999;Manning、Raghavan和Schtze 2008),使用了精确率(返回的文档中有多少是相关的)这一术语,而不是阳性预测值。召回率(找到的相关文档的比例)则被用作真正率(参见第6.3.3节)。精确率和召回率可以结合成一个称为F值的单一指标,这是它们的调和平均值。这个单一指标常用于对视觉算法进行排名(Knapitsch、Park等2017)。
任何特定的匹配策略(在特定阈值或参数设置下)都可以通过真阳性率和假阳性率来评估;理想情况下,真阳性率接近1,假阳性率接近0。随着我们改变匹配阈值,会得到一系列这样的点,这些点统称为受试者工作特征(ROC)曲线(Fawcett2006)(图7.22a)。这条曲线越接近左上角,即曲线下面积(AUC)越大,其性能越好。图7.22b展示了如何根据特征间距离绘制匹配数和非匹配数的关系图。这些曲线可以用来绘制ROC曲线(练习7.3)。ROC曲线还可以用于计算平均精度,这是在选择最佳结果时改变阈值的平均精度(PPV),然后是两个最佳结果等(见第6.3.3节和图6.27)。
使用固定阈值的问题在于难以设定;随着我们进入特征空间的不同部分,有用的阈值范围可能会有很大变化(Lowe2004;Mikolajczyk和Schmid2005)。在这种情况下,更好的策略是直接匹配特征空间中的最近邻。由于某些特征可能没有匹配项(例如,在物体识别中它们可能是背景杂波的一部分,或者在另一张图像中被遮挡),因此仍然需要使用阈值来减少假阳性的数量。
理想情况下,该阈值本身将适应特征空间的不同区域。如果可用的训练数据充足(Hua,Brown,and Winder2007),有时可以学习

图7.22 ROC曲线及其相关率:(a)ROC曲线绘制了特征提取和匹配算法特定组合下的真正率与假正率。理想情况下,真正率应接近1,而假正率接近0。ROC曲线下面积(AUC)常被用作算法性能的单一(标量)度量。或者,有时也会使用等错误率。(b)正例(匹配)和负例(非匹配)随特征间距离的变化分布。随着阈值θ的增加,真正例(TP)和假正例(FP)的数量也随之增加。
不同的特征有不同的阈值。然而,通常我们只是得到一组图像需要匹配,例如,在拼接图像或从无序的照片集合构建3D模型时(Brown和Lowe 2007,2005;Snavely、Seitz和Szeliski 2006)。在这种情况下,一个有用的启发式方法是将最近邻距离与次近邻距离进行比较,最好是从已知不匹配目标的图像中获取(例如,数据库中的不同对象)(Brown和Lowe 2002;Lowe 2004;Mishkin、Matas和Perdoch 2015)。我们可以定义这个最近邻距离比(Mikolajczyk和Schmid 2005)为
NNDR =
(7.18)
其中,d1和d2分别是最近邻和次近邻距离,DA是目标描述符,DB和DC是其最近的两个邻居(图7.23)。近期研究表明,互NNDR(或至少带有交叉一致性检查的NNDR)明显优于单向NNDR (Bellavia和Colombo 2020;Jin、Mishkin等2021)。

图7.23固定阈值、最近邻和最近邻距离比匹配。在固定距离阈值(虚线圆圈)下,描述符DA无法正确匹配DB,而DD错误地匹配了DC和DE。如果我们选择最近邻,DA正确地匹配了DB,但DD错误地匹配了DC。使用最近邻距离比(NNDR)匹配,
小NNDR d1 /d2正确匹配DA与DB,大NNDR
d/d正确
拒绝与DD匹配。
一旦我们确定了匹配策略,仍需高效地寻找潜在候选者。最简单的方法是将每对可能匹配图像中的所有特征与其他所有特征进行比较。虽然传统上这种方法计算成本过高,但现代GPU已经使得这种比较成为可能。
一种更高效的方法是设计一种索引结构,如多维搜索树或哈希表,以快速查找给定特征附近的其他特征。这些索引结构可以独立为每张图像构建(这在我们只想考虑某些潜在匹配时非常有用,例如寻找特定对象),也可以全局地为给定数据库中的所有图像构建,这样可能会更快,因为它消除了遍历每张图像的需要。对于极其庞大的数据库(数百万张或更多图像),甚至可以使用基于文档检索思想的更高效的结构,例如词汇树(Nist r和Stew nius2006)、产品量化(J gou,Douze和Schmid2010;Johnson,Douze和J gou2021)或倒排多索引(Babenko和Lempitsky2015b),具体讨论见第7.1.4节。
实现较为简单的一种技术是多维哈希,它根据应用于每个描述符向量的函数,将描述符映射到固定大小的桶中。匹配时,每个新特征都会被哈希到一个桶中,通过搜索附近的桶来返回潜在候选者,然后对这些候选者进行排序或评分,以确定哪些是有效的匹配。
哈希的一个简单例子是Brown、Szeliski和Winder使用的Haar小波
(2005)在他们的MOPS论文中。在匹配结构构建过程中,每个8×8缩放、定向和归一化的MOPS封面被转换为一个三元素索引,通过对封面的不同象限求和实现。生成的三个值根据其预期的标准差进行归一化,然后映射到两个(b=10)最近的一维区间。由这三个量化值连接形成的三维索引用于索引存储(添加)特征的23 = 8区间。查询时,仅使用主要(最近)索引,因此只需检查单个三维区间。然后可以利用该区间的系数选择k个近似最近邻以进行进一步处理(如计算NNDR)。
一种更复杂但适用范围更广的哈希方法称为局部敏感哈希,它使用独立计算的哈希函数的联合来索引特征(Gionis,Indyk和Motwani 1999;Shakhnarovich,Darrell和Indyk 2006)。Shakhnarovich、Viola和Darrell(2003)将这一技术扩展,使其对参数空间中点的分布更加敏感,他们称之为参数敏感哈希。最近的研究将高维描述子向量转换为二进制码,这些码可以通过汉明距离进行比较(Torralba,Weiss和Fergus 2008;Weiss,Torralba和Fergus 2008),或者可以适应任意核函数(Kulis和Grauman 2009;Raginsky和Lazebnik 2009)。
另一种广泛使用的索引结构是多维搜索树。其中最著名的是k-d树,也常写作kd树,它通过交替的轴对齐超平面分割多维特征空间,在每个轴上选择阈值以最大化某个标准,例如搜索树平衡(Samet 1989)。图7.24展示了一个二维k-d树的例子。这里,八个不同的数据点A至H以小菱形形式排列在二维平面上。k-d树递归地沿轴对齐(水平或垂直)切割平面分割这个平面。每次分割可以用维度编号和分割值来表示(图7.24b)。分割的安排旨在尽量平衡树,即尽可能减小其最大深度。查询时,经典的k-d树搜索首先定位查询点(+)在其相应的箱(D)中,然后在树中搜索附近的叶子节点(C,B,.. .),直到可以保证找到最近邻。最佳的箱优先(BBF)搜索(Beis和Lowe 1999)按空间距离顺序搜索箱,因此通常更高效。
许多额外的数据结构已被开发出来,用于解决精确和近似最近邻问题(Arya,Mount等,1998;Liang,Liu等,2001;Hjaltason和Samet,2003)。例如,Nene和Nayar(1997)开发了一种称为切片的技术,该技术通过沿不同维度排序的点列表进行一系列一维二分搜索。
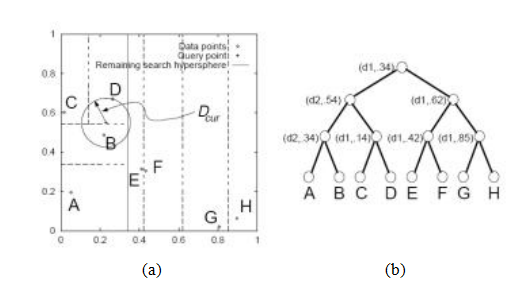
图7.24 K-d树和最佳先验(BBF)搜索(Beis和Lowe 1999)©1999 IEEE: (a)轴向切割平面的空间排列用虚线表示。单个数据点以小菱形显示。(b)相同的细分可以表示为一棵树,其中每个内部节点代表一个轴向切割平面(例如,顶部节点沿维度d1切割值为.34),每个叶节点是一个数据点。在BBF搜索过程中,查询点(记作“+”)首先在其所属的箱(D)中查找,然后在其最近的相邻箱(b)中查找,而不是在树(C).中的最近邻节点。
为了高效地筛选出位于查询点超立方体内的候选点列表。Grauman和Darrell(2005)在索引树的不同层级重新加权匹配项,这使得他们的技术对树构建中的离散化误差不那么敏感。Nist和Stew nius(2006)使用度量树,该树在层次结构的每一层将特征描述符与少量原型进行比较。由此产生
的量化视觉词汇可以与经典的信息检索(文档相关性)技术结合使用,快速从数百万图像数据库中筛选出潜在候选者(第7.1.4节)。Muja和Lowe(2009)比较了这些方法中的几种,并引入了一种新的方法(基于层次k均值树的优先搜索),并得出结论认为多重随机化k-d树通常提供最佳性能。现代计算近似最近邻的库包括FLANN (Muja和Lowe 2014)和Faiss (Johnson、Douze和J gou 2021),相关内容在Section5.1.1and附录C.2中讨论。
特征匹配验证和密集化
一旦我们有一些候选匹配,我们可以使用几何对齐(第8.1节)来验证哪些匹配是内点,哪些是外点。例如,如果我们预期整个图像在匹配视图中被平移或旋转,我们可以拟合一个全局几何

图7.25从椭圆归一化仿射区域获得的视觉词汇(Sivic和Zis- serman2009)©2009 IEEE。(a)从每一帧中提取仿射协变区域,并使用基于学习到的马氏距离的k均值聚类方法,将这些区域聚类为视觉词汇。(b)每个网格中的中心补丁显示查询点,周围的补丁显示最近邻。
转换并保留那些与估计变换足够接近的特征匹配。选择一小部分种子匹配,然后验证更大一组的过程通常称为随机抽样或RANSAC(第8.1.4节)。一旦建立了初始的一组对应关系,一些系统会寻找更多的匹配,例如沿着极线寻找额外的对应关系(第12.1节)或基于全局变换在估计位置附近寻找。还可以使用深度神经网络进行特征匹配和过滤,如Sarlin、DeTone等人(2020年)的SuperGlue系统所示。这些主题将在第8.1节和第12.2节中进一步讨论。
随着数据库中对象数量的增加(比如数十亿个对象或视频帧),将新图像与每个数据库图像匹配所需的时间可能会变得难以承受。与其逐一比较图像,需要采用技术手段快速缩小搜索范围,锁定少数可能的图像,然后通过更严格的验证阶段进行比对。
快速查找文档之间的部分匹配问题是信息检索(IR)中的一个核心问题(Baeza-Yates和Ribeiro-Neto1999;Manning,
Raghavan和Sch tze2008)。在计算机视觉中,寻找特定对象的问题
在大型集合中,称为基于内容的图像检索(CBIR)(Smeulders,Worring等,2000;Lew,Sebe等,2006;Vasconcelos,2007;Datta,Joshi等,2008)或实例检索(Zheng,Yang,和Tian,2018)。快速文档检索算法的基本方法是预先计算单个词与它们出现的文档(或网页或新闻故事)之间的倒排索引。更具体地说,特定词出现的频率
文档中的单词用于快速查找与特定查询匹配的文档。
西维克和齐瑟曼(2009)首次将红外技术应用于视觉搜索。在他们的视频谷歌系统中,首先在所有待索引的视频帧中检测仿射不变特征,这些特征既包括哈里斯特征点周围的形状适应区域(沙法利茨基和齐瑟曼2002;米科拉伊奇克和施密特2004),也包括最大稳定极值区域(马塔斯、楚姆等人2004;Section7.1.1),如图7.25a所示。接下来,从每个归一化区域计算出128维SIFT描述子(即图7.25b中的补丁)。然后,通过累积从一帧到另一帧跟踪的特征统计信息,估计这些描述子的平均协方差矩阵。随后,使用特征描述子协方差Σ定义特征描述子之间的马氏距离(5.32)。实际上,特征描述子通过预乘以Σ-1/2进行白化处理,以便可以使用欧几里得距离。5
为了将快速信息检索技术应用于图像,首先需要将每张图像中出现的高维特征描述符映射到离散的视觉词汇。Sivic和Zisserman(2003)使用k-均值聚类来完成这一映射,而一些后来的方法(Nist r和Stew nius 2006;Philbin,Chum等2007)则采用了其他技术,如词汇树或随机森林。为了使聚类时间可控,仅使用几百帧视频来学习聚类中心,这仍然涉及从大约300,000个描述符中估计数千个聚类,尽管后续研究大大扩展了这一能力(Nist r和Stew nius 2006;Philbin,Chum等2007;Mikulik,Perdoch等2013)。在视觉查询时,新查询区域中的每个特征(例如图7.25a,这是从较大视频帧裁剪出来的区域)都会映射到其对应的视觉词汇。为了防止非常常见的模式污染结果,创建了一个最常见的视觉词汇停止列表,并将这些词汇从进一步考虑中剔除。
一旦查询图像或区域被映射为其构成的视觉词汇,就需要从数据库中检索出可能匹配的图像。具体操作方法可参见Sivic和Zisserman(2009)、Nist r和Stew nius(2006)、Philbin、Chum等人(2007)、Chum、Philbin等人(2007)、Philbin、Chum
等人(2008),以及本书第一版(Szeliski2010,第14.3.2节)。由于量化和评分特征的高效性,Nist r和Stew nius(2006)构建的基于词汇树的识别系统能够实时处理来自40,000张CD封面的数据库,并以1赫兹的速度匹配包含一百万帧的数据库。
5注意,从匹配的特征点计算特征协方差比在描述子空间上简单地执行PCA要合理得多(Winder和Brown2007)。这大致相当于我们在第5.2.3节中研究的类内散射矩阵。

图7.26使用随机树进行位置或建筑物识别(Philbin,Chum等人,2007)©2007 IEEE。左图是查询,其他图是最高排名的结果。
取自六部故事片。
实例识别系统在2000年代继续迅速改进。Philbin、Chum等人(2007)展示了随机森林k-d树在大规模位置识别任务中表现优于词汇树(图7.26)。他们还比较了验证阶段使用不同二维运动模型的效果(第2.1.1节)。后续工作中,Chum、Philbin等人(2007)应用了信息检索中的另一个概念,即查询扩展,这涉及将初始查询中排名靠前的图像重新提交作为额外查询,以生成更多的候选结果。Philbin、Chum等人(2008)展示了如何通过软分配来缓解视觉词汇选择中的量化问题,其中每个特征描述符映射到多个附近的视觉词汇,类似于J gou、Harzallah和Schmid(2007)之前提出的多分配想法。然而,这些技术往往会减少视觉词汇向量的稀疏性并增加内存和计算成本。J gou、Douze和Schmid(2008)在初始大规模图像排序阶段引入了部分几何信息和局部描述符之间的显式
匹配方案。综上所述,这些算法帮助实例识别算法实现了网络规模的检索、匹配和三维重建任务(Agarwal、Furukawa等人,2010,2011;Frahm
自2012年的“深度学习革命”以来,研究人员开始开发神经特征检测器和描述符(第7.1.1节和第7.1.2节),有时将它们组合成端到端匹配系统。图7.27展示了实例检索的一些主要里程碑,而图7.28则展示了各种不同的经典和基于CNN的检索架构。郑、杨和田(2018)的综述论文更详细地描述并对比了这些不同的算法,还提供了
6查询扩展的另一种方法是数据库端增强(Arandjelovi和Zisserman2012)。
但请注意,一些流行的开源大规模重建系统,如COLMAP,仍然使用传统特征和索引方案(Sch nberger和Frahm2016)。

图7.27实例检索中的里程碑(Zheng、Yang和Tian2018)©2018 IEEE,显示了从手工制作的基于特征的检索到基于CNN的方法的转变。

这些算法在图像检索数据集上的实验比较。您还可以在第6.2.3节关于视觉相似性搜索的部分找到更多相关技术和系统的详细信息,该部分讨论了用单个向量表示图像的全局描述符(Arandjelovic,Gronat等2016;Radenovi,Tolias和Chum 2019;Yang,Kien Nguyen等2019;Cao,Araujo和Sim 2020;Ng,Balntas等2020
;Tolias,Jenicek和Chum 2020),作为局部特征包的替代方案;第11.2.3节关于位置识别的部分;以及第11.4.6节关于从社区(互联网)照片中进行大规模3D重建的部分。
一种替代方法是,在第一张图像中找到一组可能的特征位置,然后在后续图像中搜索这些位置对应的特征。这种检测后跟踪的方法更广泛应用于视频跟踪场景,预期相邻帧之间的运动和外观变形量较小。
选择好的特征进行跟踪的过程与为更广泛的识别应用选择好的特征密切相关。实际上,包含双向高梯度的区域,即在自相关矩阵(7.8)中具有高特征值的区域,提供了稳定的位置来寻找对应关系(Shi和Tomasi 1994)。
在后续帧中,寻找对应补丁平方差较低的位置(7.1)通常效果良好。然而,如果图像发生亮度变化,则明确补偿这种变化(9.9)或使用归一化互相关(9.11)可能更为合适。如果搜索范围较大,使用层次搜索策略通常更高效,该策略利用低分辨率图像中的匹配来提供更好的初始猜测,从而加快搜索速度(第9.1.1节)。替代策略包括学习被跟踪补丁的外观特征,然后在其预测位置附近进行搜索(Avidan2001;Jurie和Dhome 2002;Williams、Blake和Cipolla2003)。这些主题在第9.1.3节中有更详细的讨论。
如果特征在较长的图像序列中被跟踪,其外观可能会发生更大的变化。这时你需要决定是继续与最初检测到的补丁(特征)匹配,还是在每个后续帧的匹配位置重新采样。前者容易失败,因为原始补丁可能会发生外观变化,如缩短。后者则存在特征从其原始位置漂移到图像中其他位置的风险(Shi和Tomasi 1994)。(从数学上讲,小的失配误差会累积形成马尔可夫随机游走,导致随时间推移更大的漂移。)

图7.29使用仿射运动模型进行特征跟踪(Shi和Tomasi 1994)©1994 IEEE,上排:跟踪特征位置周围的图像块。下排:使用仿射变换回拉回第一帧后的图像块。尽管速度标志从一帧到另一帧逐渐变大,但仿射变换仍保持了原始帧与后续跟踪帧之间的良好相似性。
一个理想的解决方案是使用仿射运动模型(第9.2节)将原始补丁与后续图像位置进行比较。Shi和Tomasi(1994)首先使用平移模型比较相邻帧中的补丁,然后利用这一步骤产生的位置估计值初始化当前帧中补丁与首次检测到特征的基帧之间的仿射配准(图7.29)。在他们的系统中,特征仅在跟踪失败的区域偶尔被检测到。通常情况下,会在特征当前预测位置周围搜索一个区域,并使用增量配准算法(第9.1.3节)。由此产生的跟踪器常被称为Kanade-Lucas-Tomasi(KLT)跟踪器。
自他们最初进行特征跟踪研究以来,石和托马西的方法已经催生了大量后续论文和应用。比尔斯利、托尔和齐瑟曼(1996)利用扩展特征跟踪结合运动结构(第11章)从视频序列中逐步构建稀疏3D模型。康、斯泽利斯基和舒姆(1997)将相邻(规则网格化)补丁的角点连接起来,以提高跟踪的稳定性,但代价是处理遮挡时表现较差。托马西尼、富西埃洛等人(1998)为基本的石和托马西算法提供了一个更好的虚假匹配拒绝标准,柯林斯和刘(2003)提供了改进的特征选择机制和应对长时间内较大外观变化的方法,沙菲克和沙(2005)开发了适用于大量移动对象或点的视频特征匹配(数据关联)算法。勒佩蒂和富亚(2005)以及伊尔马兹、贾韦德和沙(2006)综述了更广泛的物体跟踪领域,该领域不仅包括基于特征的技术,还包括基于轮廓和区域的替代技术(第7.3节)。

图7.30使用快速训练分类器进行实时头部跟踪(Lepetit、Pilet和Fua
特征跟踪的最新发展是使用学习算法构建专用识别器,以快速搜索图像中的匹配特征(Lepetit、Pilet和Fua2006;Hinterstoisser、Benhimane等人2008;Rogez、Rihan等人。
2008;zuysal,Calonder等人2010)。通过花时间在样本补丁上训练分类器
并且通过仿射变形,可以构建极其快速且可靠的特征检测器,从而支持更快的运动(图7.30)。将这些特征与可变形模型(Pilet、Lepetit和Fua2008)或从运动中构建结构的算法(Klein和Murray2008)相结合,可以实现更高的稳定性。
虽然基于特征的跟踪在实时应用中仍被广泛使用,如SLAM、自主导航和增强现实(第11.5节),但目前许多关于跟踪的研究集中在整体物体跟踪上(Chellappa,Sankaranarayanan等2010;Smeulders,Chu等2014),我们将在Section9.4.4中详细探讨这一主题。
快速特征跟踪最引人注目的应用之一是性能驱动的动画,即基于跟踪用户运动的3D图形模型的交互变形(Williams1990;Litwinowicz和Williams1994;Lepetit、Pilet和Fua2004)。
巴克、芬克尔斯坦等人(2000)提出了一种系统,该系统能够跟踪用户的面部表情和头部动作,并利用这些信息在一系列手绘草图之间进行变形。动画师首先提取每个草图的眼睛和嘴巴区域,并在每张图像上绘制控制线(图7.31a)。运行时,面部跟踪系统(Toyama 1998)确定这些特征的当前位置(图7.31b)。动画系统决定哪个

图7.31表现驱动的手绘动画(Buck,Finkelstein等2000)©2000 ACM:(a) eye和嘴部部分的手绘草图及其叠加的控制线;(b)输入视频帧中叠加了跟踪特征;(c)不同的输入视频帧及其对应的(d)手绘动画。
输入图像根据最近邻特征外观匹配和三角形重心插值进行变形。它还从跟踪的特征中计算头部的整体位置和方向。最终变形的眼睛和嘴巴区域被重新合成到整体头部模型中,生成手绘动画的一帧(图7.31d)。
在最近的研究中,巴恩斯、雅各布斯等人(2008)观察用户在桌面上用纸剪动画,然后将这些动作和图画转化为无缝的二维动画。基于特征的人脸追踪器继续被广泛使用(佐尔费尔、蒂斯等人,2018),不仅在视觉特效行业,还用于实时智能
手机增强现实效果,如脸书的Spark AR面具。
虽然兴趣点对于找到可以在二维中精确匹配的图像位置很有用,但边缘点更为丰富,通常携带重要的语义关联。例如,物体的边界,在三维中也对应于遮挡事件,通常由可见轮廓界定。其他类型的边缘则对应于阴影边界或折痕边缘,这些地方表面方向迅速变化。孤立的边缘点也可以组合成长曲线或轮廓,以及直线段(第7.4节)。有趣的是,即使是年幼的孩子也能轻松识别出熟悉的物体或动物,即使它们只是简单的线条画。

图7.32人边界检测(Martin、Fowlkes和Malik2004)©2004 IEEE。边缘的暗度对应于有多少人标记了该位置的对象边界。
给定一张图像,我们如何找到显著的边缘?考虑图7.32中的彩色图像。如果有人让你指出最“显著”或“最强”的边缘或物体边界,你会追踪哪些?你的感知与图7.32中显示的边缘图像有多接近?
定性地说,边缘出现在不同颜色、强度或纹理区域的边界处(Martin,Fowlkes和Malik 2004;Arbel ez,Maire等2011;Pont-Tuset,Arbel ez等2017
)。不幸的是,将图像分割
成连贯的区域是一项艰巨的任务,我们将在第7.5节中讨论。通常,最好仅使用局部信息来检测边缘。
在这种情况下,一种合理的方法是将边缘定义为强度或颜色变化迅速的位置。可以将图像看作是一个高度场。在这样的表面上,边缘出现在陡峭斜坡的位置,或者等效地,在密集的等高线区域(地形图上)。
定义曲面斜率和方向的数学方法是通过它的梯度,
(7.19)
局部梯度向量J指向强度函数中上升最快的方位。其大小表示变化的斜率或强度,而其方向则指向与局部轮廓垂直的方向。
不幸的是,取图像导数会突出高频部分,从而放大噪声,因为噪声与信号的比例在高频部分更大。因此,这是明智的做法
为了在计算梯度之前用低通滤波器平滑图像。由于我们希望边缘检测器的响应与方向无关,因此需要一个圆形对称的平滑滤波器。正如我们在第3.2节中所见,高斯滤波器是唯一可分离的圆形对称滤波器,因此它被用于大多数边缘检测算法。Canny(1986)讨论了其他滤波器,许多研究人员回顾了不同的边缘检测算法并比较了它们的性能(Davis 1975;Nalwa和Binford 1986;Nalwa 1987;Deriche 1987;Freeman和Adelson 1991;Nalwa 1993;Heath、Sarkar等1998;Crane 1997;Ritter和Wilson 2000;Bowyer、Kranenburg和Dougherty 2001;Arbel ez、Maire等2011;Pont-Tuset、Arbel ez等2017)。
由于微分是一个线性运算,因此它与其他线性滤波运算可以互换。因此,平滑图像的梯度可以写为
Jσ (x) = ▽[Gσ (x) * I(x)] = [▽Gσ ](x) * I(x), (7.20)
即,我们可以将图像与高斯核函数的水平和垂直导数进行卷积,
▽Gσ (x
)
= , (x) = [—x — y
] exp (— ,
(7.21)
参数σ表示高斯函数的宽度。这与Freeman和Adelson(1991)在第3.2.3节中已经介绍的第一阶可导向滤波器的计算相同。
然而,对于许多应用而言,我们希望将这种连续的梯度图像简化为仅包含孤立的边缘,即沿边缘轮廓在离散位置上的单个像素。这可以通过寻找与边缘方向垂直的方向上的最大值来实现,即沿着梯度方向。
找到这个最大值相当于沿着梯度方向对强度场求方向导数,然后寻找零交叉点。所需的向量导数等同于第二个梯度算子与第一个结果之间的点积,
Sσ (x) = ▽ · Jσ (x) = [▽2 Gσ ](x) * I(x). (7.22)
▽2 Gσ
(7.23)
因此,该核被称为高斯(LoG)拉普拉斯核(Marr和Hildreth1980)。该核可以分为两个可分离的部分,
▽2 Gσ (x) = —
Gσ
(y)Gσ (x) (7.24)
(Wiejak、Buxton和Buxton1985),这允许使用可分离过滤实现更高效的实施(第3.2.1节)。
在实际应用中,通常会用高斯差分(DoG)计算来替代高斯卷积的拉普拉斯算子,因为它们的核形状在定性上是相似的(Figure3.34)。如果已经计算了“拉普拉斯金字塔”(第3.5节),这种方法尤为方便。
事实上,在计算边缘场时,并不一定非要区分相邻层次之间的差异。想想“广义”高斯差分图像中的零交叉点代表什么。更精细(小核)的高斯函数是原始图像的降噪版本。较粗(大核)的高斯函数则是较大区域平均强度的估计值。因此,每当DoG图像改变符号时,这对应于(略微模糊的)图像从相对暗处变为相对亮处,相对于该邻域内的平均强度而言。
一旦我们计算了符号函数S(x),就必须找到其零交叉点,并将其转换为边缘元素(edgels)。检测和表示零交叉点的一个简单方法是寻找相邻像素位置xi和xj,其中符号值发生变化,即[S(xi)> 0] [S(xj)> 0]。
这个交叉点的子像素位置可以通过计算连接S(xi)和S(xj)的“线”的“x轴截距”来获得,
(7.25)
通过线性插值在原始像素网格上计算的梯度值,可以获得这种边缘的方向和强度。
通过将对偶网格上的相邻边缘连接到由四个相邻像素组成的原始像素网格中的每个正方形内的形成边缘,可以获得一种替代的边缘表示。这种表示的优势在于,边缘现在位于比原始像素网格偏移半个像素的网格上,因此更容易存储和访问。与之前一样,可以通过插值梯度场或从高斯图像差异中估计这些值来计算边缘的方向和强度(见练习7.7)。
在对边缘方向的准确性要求较高的应用中,可以使用高阶可转向滤波器(Freeman和Adelson1991)(参见Section3.2.3)。这种滤波器对更细长的边缘具有更高的选择性,并且有可能更好地建模曲线。
8回顾Burt和Adelson(1983a)的“拉普拉斯金字塔”实际上计算高斯滤波水平的差异。
9该算法是三维行进立方体等值面提取算法(Lorensen和Cline)的二维版本
图7.33边缘检测尺度选择(Elder和Zucker 1998)©1998 IEEE:((a))原始图像;(b-c)调整至更精细(模特)和更粗略(阴影)尺度的Canny/Deriche边缘检测器;(d)梯度估计的最小可靠尺度;(e)二阶导数估计的最小可靠尺度;(f)最终检测到的边缘。
交点,因为它们可以表示同一像素上的多种方向(图3.16)。它们的缺点是计算成本更高,且边缘强度的方向导数没有简单的闭式解。10
尺度选择和模糊估计
正如我们之前提到的,导数、拉普拉斯和高斯差分滤波器(7.20-7.23)都需要选择一个空间尺度参数σ。如果我们只关注检测锐利边缘,滤波器的宽度可以从图像噪声特性中确定(Canny1986;Elder和Zucker1998)。然而,如果我们希望检测不同分辨率下的边缘(图7.33b-c),可能需要采用一种尺度空间方法,该方法能够检测并选择不同尺度下的边缘(Witkin1983;Lindeberg1994,1998a;Nielsen,Florack和Deriche1997)。
埃尔德和祖克(1998)提出了一种解决此问题的原则方法。给定已知的图像噪声水平,他们的技术计算每个像素可以可靠检测到边缘的最小尺度(图7.33d)。该方法首先通过选择不同尺度下计算的梯度估计值中的梯度幅度来密集地计算图像上的梯度。然后,它对有向二阶导数进行类似的最小尺度估计,并利用这一量的零交叉点稳健地选择边缘(图7.33e-f)。作为可选的最后一步,可以从二阶导数响应中极值之间的距离减去高斯滤波器的宽度来计算每条边的模糊宽度。
色彩边缘检测
虽然大多数边缘检测技术都是为灰度图像开发的,但彩色图像可以提供额外的信息。例如,不同亮度的颜色(具有相同亮度的颜色)之间的明显边缘是有用的线索,但是不能被灰度边缘运算符检测到。
一种简单的方法是将每个颜色通道单独运行的灰度检测器的输出结合起来。然而,需要注意一些事项。例如,如果我们简单地将每个颜色通道中的梯度相加,带符号的梯度可能会相互抵消!(比如考虑一个纯红到绿的边缘。)我们也可以独立地在每个通道中检测边缘,然后取这些边缘的并集,但这可能导致难以连接的粗化或重叠的边缘。
更好的方法是在每个频带中计算定向能量(Morrone和Burr 1988;Perona和Malik 1990a),例如使用二阶可导向滤波器(第3.2.3节)(Freeman和Adelson 1991),然后将定向加权能量相加,找到它们的联合最佳方向。不幸的是,这种能量的方向导数可能没有封闭形式的解(如带符号的一阶可导向滤波器的情况),因此不能使用简单的零交叉策略。然而,Elder和Zucker(1998)描述的技术可以用来数值计算这些零交叉点。
一种替代方法是在每个像素周围估计局部颜色统计(Ruzon和Tomasi 2001;Martin、Fowlkes和Malik 2004)。这种方法的优点在于可以使用更复杂的技术(例如,三维颜色直方图)来比较区域统计,并且还可以考虑其他指标,如纹理。图7.34显示了此类检测器的输出。
多年来,为了检测颜色边缘,人们开发了许多其他方法,可以追溯到Nevatia(1977)的早期工作。Ruzon和Tomasi(2001)以及Gevers、van de Weijer和Stokman(2006)对这些方法进行了很好的综述,其中包括融合多通道输出、使用多维梯度和基于向量的方法等思想。
结合边缘特征线索
如果边缘检测的目标是匹配人类边界检测的性能(Bowyer,Kranenburg和Dougherty 2001;Martin,Fowlkes和Malik 2004;Arbel ez,Maire等2011;Pont-Tuset,Arbel ez等2017),而
不仅仅是寻找用于匹配的稳定特征,
那么通过结合亮度、颜色和纹理等多低级线索,可以构建出更好的检测器。
马丁、福尔克斯和马利克(2004)描述了一个系统,该系统结合了亮度、颜色和纹理边缘,以在手段分割的自然彩色图像数据库上实现最先进的性能(马丁、福尔克斯等人,2001)。首先,他们构建并训练了独立的方向半圆检测器,用于测量亮度(亮度)、颜色(a*和b*通道,总响应)和纹理(未归一化的滤波器组响应,来自马利克、贝隆吉等人(2001)的工作)中的显著差异。然后,使用软非极大值抑制技术对某些响应进行锐化。最后,利用多种机器学习技术将三个检测器的输出结合起来,其中逻辑回归被发现具有速度、空间和准确性之间的最佳平衡。结果系统(见图7.34的一些示例)显示出优于先前开发的技术。梅尔、阿尔贝莱兹等人(2008)通过结合基于局部外观的检测器与光谱(基于分割的)检测器(贝隆吉和马利克,1998)改进了这些结果。在后续工作中,阿尔贝莱兹、梅尔等人(2011)建立了层次化分割。
7.2.2轮廓检测
虽然孤立的边缘对于各种应用很有用,例如线检测(第7.4节)和稀疏立体匹配(第12.2节),但当它们被链接到连续轮廓时,它们变得更加有用。
如果边缘是通过某个函数的零交叉点检测到的,那么将它们连接起来就很简单了,因为相邻的边缘点共享共同的端点。将这些边缘点链接成链涉及拾取一个未连接的边缘点,并沿着其邻居双向追踪。可以使用一个排序后的边缘点列表(首先按x坐标排序,然后按y坐标排序,以

图7.34综合亮度、颜色、纹理边界检测器(Martin,Fowlkes和Malik 2004)©2004 IEEE。连续几行显示了亮度梯度(BG)、颜色梯度(CG)、纹理梯度(TG)以及综合(BG+CG+TG)检测器的输出结果。最后一行显示了从手段分割图像数据库中的人工标注边界(Martin,Fowlkes等2001)。

图7.35链接轮廓的一些编码替代方案。(a)网格对齐的链接边缘链的链码表示。该代码以一系列方向码的形式表示,例如0 1 0 7 6 5,这些方向码可以进一步使用预测编码和行程长度编码进行压缩。(b–c)轮廓的弧长参数化。沿轮廓(b)的离散点首先被转换为沿弧长的(c)(x,y)对。然后,这条曲线可以定期重新采样或转换为其他(例如傅里叶)表示形式。
例如),可以使用二维数组来加速邻居查找。如果边缘不是通过零交叉检测到的,那么找到边缘的延续会变得很棘手。在这种情况下,比较相邻边缘的方向(以及可选的相位)可以用于消除歧义。连接组件计算的一些想法有时也可以用来使边缘链接过程更快(见练习7.8)。
一旦边缘像素被连接成链,我们可以应用一个可选的具有滞后性的阈值处理,以去除强度较低的轮廓段(Canny1986)。滞后性的基本思想是设置两个不同的阈值,允许被跟踪的曲线在高于较高阈值的情况下强度下降到较低阈值。
连接的边缘列表可以使用多种替代表示方法更紧凑地编码。链码使用三位代码对应于点与其后继点之间的八个基本方向(北、东北、东、东南、南、西南、西、西北),来编码位于N8网格上的连接点列表(图7.35a)。虽然这种表示比原始的边缘列表更为紧凑(特别是当使用预测可变长度编码时),但它不太适合进一步处理。
一个更有用的表示方法是轮廓的弧长参数化,x(s),其中s表示沿曲线的弧长。考虑图7.35b中所示的边集。我们从一个点开始(图7.35c中的(1.0,0.5)的点),并在坐标s = 0处绘制它(图7.35c)。下一个点(2.0,0.5)在s = 1处绘制,再下一个点(2.5,1.0)在s = 1.7071处绘制,即我们以每个边段的长度递增。最终的图可以在进一步处理之前,在规则的(例如,整数)s网格上重新采样。

图7.36使用弧长参数化匹配两条轮廓。如果两条曲线都归一化到单位长度,s∈[0,1]并以它们的质心x0为中心,它们将具有相同的描述符,直到一个整体的“时间”偏移(由于s=0的不同起点)和相位(x-y)偏移(由于旋转)。

图7.37使用高斯核进行曲线平滑(Lowe1988)©1998 IEEE:(a)不使用收缩校正项;(b)使用收缩校正项。
处理
弧长参数化的优点在于它使得匹配和处理(例如平滑)操作变得更加容易。考虑图7.36中描述相似形状的两条曲线。为了比较这两条曲线,我们首先从每个描述符中减去平均值x0 = ,sx(s)。接下来,我们将每个描述符重新缩放,使s从0到1而不是从0到S,即x(s)除以S。最后,我们将每个归一化的描述符进行傅里叶变换,将每个x =(x,y)值视为复数。如果原始曲线相同(仅相差未知的比例和旋转),那么最终的傅里叶变换结果应该只在幅度上有所不同,加上由于旋转引起的恒定复相位偏移,以及由于s的不同起点而在域内产生的线性相位偏移(见练习7.9)。
弧长参数化也可用于平滑曲线以去除数字化

图7.38不影响曲线扫掠的曲线特性变化(Finkelstein和Salesin1994)©1994 ACM:高频小波可以用风格库中的示例替换,以产生不同的局部外观。
噪声。然而,如果我们仅仅应用一个常规平滑滤波器,曲线往往会向内收缩(图7.37a)。Lowe(1989)和Taubin(1995)描述了通过基于二阶导数估计或更大的平滑核添加偏移项来补偿这种收缩的技术(图7.37b)。芬克尔斯坦和塞利辛(1994)提出了一种基于小波分解中选择性修改不同频率的替代方法。除了控制收缩而不影响其“范围”外,小波还允许交互式地修改曲线的“特征”,如图7.38所示。
曲线的平滑和简化过程与“草火”(距离)变换和区域骨架(第3.3.3节)(Tek和Kimia 2003)有关,可用于根据轮廓形状识别物体(Sebastian和Kimia 2005)。此外,还可以使用更局部的曲线形状描述符,如形状上下文(Belongie、Malik和Puzicha 2002),这些描述符在识别过程中可能对因遮挡导致的部分缺失更为鲁棒。
轮廓检测与链接领域持续快速进化,现在包括全局轮廓分组、边界完成和节点检测(Maire,Arbelaez等2008),以及将轮廓分组到可能的区域(Arbel ez,Maire等2011)和宽基线对应(Meltzer和Soatto 2008)。一些涉及轮廓检测的其他论文包括Xiaofeng和Bo
(2012),Lim,Zitnick和Doll r(2013),Doll r和Zitnick(2015),Xie和Tu(2015),以及Pont-Tuset,Arbel ez等(2017)。
虽然边缘可以作为对象识别或匹配特征的组件,但它们也可以直接用于图像编辑。
事实上,如果在保留每个边缘的同时保留边缘的幅度和模糊估计值,视觉上

图7.39在轮廓域中的图像编辑(Elder和Goldberg2001)©2001 IEEE:
(a)和(d)原始图像;(b)和(e)提取的边缘(要删除的边缘用白色标记);(c)和(f)重建的编辑图像。
可以从这些信息中重建出类似的图像(Elder1999)。基于这一原理,Elder和Goldberg(2001)提出了一种“轮廓域图像编辑”系统。该系统允许用户选择性地移除与不需要的特征相对应的边缘,如镜面反射、阴影或分散注意力的视觉元素。通过从剩余的边缘重建图像,不希望的视觉特征已被移除(图7.39)。
另一个潜在应用是增强感知显著的边缘,同时简化底层图像以生成卡通或“钢笔画”风格化图像(DeCarlo和Santella2002)。该应用在第10.5.2节中进行了更详细的讨论。
虽然直线、消失点和矩形在人造世界中很常见,但对应于物体边界的曲线更为常见,尤其是在自然环境中。在本节中,我们将介绍一些定位图像中边界曲线的方法。
第一个曲线最初由其发明者(Kass、Witkin和Terzopoulos1988)称为蛇形曲线(第7.3.1节),是一种能量最小化二维样条曲线,可演化(移动)
朝向图像特征,如强边缘。第二种智能剪刀(Mortensen和Barrett 1995)(Section7.3.1),允许用户实时勾勒出一条贴合物体边界的曲线。最后,水平集技术(第7.3.2节)通过将曲线作为特征函数的零集来演化,这使得它们能够轻松改变拓扑结构并融入基于区域的统计信息。
这三种方法都是活动轮廓的例子(Blake和Isard 1998;Mortensen 1999),因为这些边界检测器在图像和可选用户引导力的共同作用下,逐步向最终解移动。下面的介绍大幅简化了本书第一版中第5.1节的内容(Szeliski 2010),感兴趣的读者可以查阅更多细节。
蛇形曲线是第4.2节中首次介绍的一维能量最小化样条的二维推广,
εint = ∫ α(s)Ⅱfs (s)Ⅱ2 + β(s)Ⅱfss (s)Ⅱ2 ds, (7.26)
其中s是沿曲线f(s) =(x(s),y(s))的弧长,α(s)和β(s)是类似于(4.24–4.25)中引入的s(x,y)和c(x,y)项的一阶和二阶连续性加权函数。我们可以通过沿初始曲线位置均匀采样来离散化这一能量(图7.35c),以获得
(7.27)
+ β(i)Ⅱf(i + 1) - 2f(i) + f(i - 1)Ⅱ2 /h4 ,
其中是步长,如果我们在每次迭代后沿着弧长重采样曲线,就可以忽略它。
除了这种内部的样条能量之外,蛇同时最小化基于图像和基于约束的外部势能。基于图像的势能是几个项的总和
εimage = wline εline + wedge εedge + wterm εterm, (7.28)
其中,线项将蛇吸引到暗色的脊上,边缘项将蛇吸引到强烈的梯度(边缘)上,而项则将蛇吸引到线的末端。随着蛇的进化,
为了减少能量,它们经常“扭动”和“滑行”,这就是它们的流行名称。

图7.40弹性网络:开放的方块表示城市,封闭的方块通过直线段连接的是游览点。蓝色圆圈表示每个城市的吸引力范围,这种吸引力会随时间减弱。根据弹性网络的贝叶斯解释,蓝色圆圈对应于从某个未知游览点生成每个城市的圆形高斯分布的一个标准差。
因为普通蛇形模型有收缩的趋势,通常最好通过将蛇形模型绘制在要跟踪的对象外部来初始化。或者,可以向动力学中加入膨胀力(Cohen和Cohen 1993),即沿每个点的法线向外移动。此外,还可以用深度神经网络替代能量最小化变分演化方程,以显著提高性能(Peng、Jiang等2020)。
弹性网和滑动弹簧
一个有趣的蛇形变体,最初由杜宾和威尔肖(1987)提出,后来杜宾、斯泽利斯基和尤尔(1989)在能量最小化框架下重新表述,是旅行商问题(TSP)的弹性网公式。回想一下,在TSP中,旅行商必须访问每个城市一次,同时尽量减少总行走距离。一条被限制通过每个城市的蛇可以解决这个问题(尽管没有最优性保证),但事先无法确定每条蛇控制点应与哪个城市关联。
而不是在蛇节点和城市之间设置固定的约束,假设城市会在游览路线(Figure7.40)上的某个点附近经过。从概率的角度来看,每个城市都是以每个游览点为中心的高斯混合生成的,
p
ij与pij = e-d
| 469 | |
| 其中σ是高斯分布的标准差 | |
| dij = Ⅱf(i) - d(j)Ⅱ | (7.30) |
是巡游点f(i)和城市位置d(j)之间的欧几里得距离。相应的数据拟合能量(负对数似然)是
这种能量的名称来源于,与普通的弹簧不同,普通弹簧将给定的蛇形点与给定的约束条件耦合,而这种替代能量定义了一个滑动弹簧,使得约束条件(城市)和曲线(路线)之间的关联随时间演变(Szeliski1989)。请注意,这是广受欢迎的迭代最近点数据约束的一种软变体,通常用于拟合或对齐表面到数据点或彼此之间(第13.2.1节)(Besl和McKay1992;Chen和Medioni1992;Zhang1994)。
为了计算出一个良好的TSP解决方案,滑动弹簧数据关联能量与常规的一阶内部平滑能量(7.27)相结合,以定义一条路径的成本。路径f(s)最初被初始化为围绕城市点平均值的小圆圈,而σ逐渐降低(图7.40)。当σ值较大时,路径试图靠近点的质心;但随着σ的减小,每个城市对其最近的路径点的吸引力越来越强(Durbin,Szeliski,和Yuille 1989)。当σ→0时,每个城市至少会捕获一个路径点,且后续城市的路径变得直线。
虽然蛇在捕捉许多真实世界轮廓的细微和不规则细节方面非常擅长,但它们有时会表现出太多的自由度,这使得它们在进化过程中更容易陷入局部最小值。
解决此问题的一个方法是通过使用B样条近似来控制具有较少自由度的蛇形曲线(Menet、Saint-Marc和Medioni1990b,a;Cipolla和Blake1990)。由此产生的B蛇形曲线可以表示
(7.32)
如果被跟踪或识别的对象在位置、尺度或方向上有很大的变化,这些可以建模为控制点上的附加变换,例如,
x = sRxk + t(2.18),该值可与对照组的值同时进行估计
或者,可以运行单独的检测和对准阶段,首先定位和定向感兴趣对象(Cootes、Cooper等人,1995)。

图7.41活动形状模型(ASM):(a)改变一组面部的前四个形状参数的效果(Cootes,Taylor等人,1993年)©1993 IEEE;(b)沿每个控制点法线寻找最强梯度(Cootes,Cooper等人,1995年)©1995 Elsevier.
在B型蛇形线中,由于蛇形线受控自由度较少,因此不需要使用原始蛇形线的内部平滑力,尽管这些平滑力仍可以通过有限元分析推导和实现,即对B样条基函数求导和积分(Terzopoulos1983;Bathe2007)。
在实际应用中,通常会估计一组关于控制点{xk }的形状先验分布(Cootes,Cooper等,1995)。描述这一分布的一种方法是通过每个单独点xk的位置x-k和二维协方差Ck来表示。这些可以转化为对点位置的二次惩罚(先验能量)。然而,在实践中,点位置的变化通常是高度相关的。
一种优选的方法是同时估计所有点的联合协方差。首先,将所有点的位置{xk }连接成一个向量x,例如通过交错每个点的x和y位置。这些向量在所有训练样本中的分布可以用均值x和协方差来描述。
(7.33)
其中,xp是P个训练样本。使用特征值分析(附录A.1.2),可以得到
也称为主成分分析(PCA)(Section5.2.3和附录B.1),协方差矩阵可以写为,
C = Φ diag(λ0... λK - 1) ΦT . (7.34)
在大多数情况下,可以使用具有最大特征值的少数几个特征向量来模拟点的可能出现。所得点分布模型(Cootes、Taylor等人,1993;Cootes、Cooper等人,1995)可表示为
x = x- + b, (7.35)
其中b是M冬K元素形状参数向量,是Φ的前m列。
为了将形状参数限制在合理的值,我们可以使用形式如下的二次惩罚
或者,允许的bm值范围可以限制在某个范围内,例如,jbmj≤3√λm(Cootes,Cooper等,1995)。Isard和Blake(1998)回顾了推导一组形状向量的替代方法。通过在-2√λm≤2√λm的范围内变化各个形状参数bm,可以很好地表示预期的外观变化,如图7.41a所示。
为了使点分布模型与图像对齐,每个控制点会在垂直于轮廓的方向上搜索,以找到最可能对应的图像边缘点(图7.41b)。这些单独的测量结果可以与形状参数(以及位置、尺度和方向参数,如需)的先验知识结合,来估计一组新的参数。由此产生的活动形状模型(ASM)可以通过迭代最小化来拟合非刚性变形物体的图像,例如医学图像或身体部位,如手部(Cootes,Cooper等,1995)。ASM还可以与底层灰度分布的主成分分析相结合,创建活动外观模型(AAM)(Cootes,Edwards,和Taylor,2001),我们在Section6.2.4中对此进行了更详细的讨论。
动态蛇形线和冷凝
在许多活动轮廓的应用中,感兴趣的对象在变形和演化过程中从一帧到另一帧被跟踪。在这种情况下,使用前一帧的估计值来预测和限制新的估计值是有意义的。
一种方法是使用卡尔曼滤波,这将产生一个称为卡尔曼蛇的公式(Terzopoulos和Szeliski1992;Blake、Curwen和Zisserman1993)。卡尔曼滤波基于形状参数演化的线性动态模型,
xt = Axt - 1 + wt , (7.37)
其中xt和xt - 1是当前和前一状态变量,A是线性转换矩阵,w是一个噪声(扰动)向量,通常建模为高斯(Gelb

图7.42使用冷凝进行头部跟踪(Isard和Blake,1998)©1998
Springer:(a)头部估计分布的样本集表示;(b)每个控制顶点位置的多个测量值;(c)多假设跟踪随时间变化。
1974)。矩阵A和噪声协方差可以通过观察被跟踪对象的典型序列提前学习(Blake和Isard1998)。
然而,在许多情况下,例如在杂乱环境中跟踪时,如果我们移除假设分布为高斯分布这一前提,可以得到更好的轮廓估计。在这种情况下,传播的是一个通用的多模态分布。为了建模这种多模态分布,Isard和Blake(1998)将粒子滤波技术引入了计算机视觉领域。粒子滤波技术通过一组加权点样本来表示概率分布(Andrieu、de Freitas等2003;Bishop 2006;Koller和Friedman 2009)。
为了根据线性动力学(确定性漂移)更新样本的位置,首先更新样本的中心,并为每个点生成多个样本。然后对这些样本进行扰动以考虑随机扩散,即它们的位置由从w分布中抽取的随机向量移动。最后,将这些样本的权重乘以测量概率密度,即根据当前(新的)测量结果,计算每个样本的似然性。由于点样本代表并传播了多模态密度的条件估计,Isard和Blake(1998)将其算法称为条件密度传播或凝聚。 图7.42a显示了头部跟踪器的一个分解样本可能的样子,为被跟踪的(子集)粒子绘制红色B样条轮廓。图7.42b显示了为什么测量密度本身通常是多模态的:边缘的位置
12多模态分布建模的替代方法包括高斯混合(第5.2.2节)和多重假设跟踪(Bar-Shalom和Fortmann1988;Cham和Rehg1999)。
13注意,由于这些步骤的结构,可以使用非线性动力学和非高斯噪声。

图7.43智能剪刀:(a)当鼠标追踪白色路径时,剪刀沿着物体边界跟随橙色路径(绿色曲线显示中间位置)(Mortensen和Barrett 1995)©1995 ACM;(b)常规剪刀有时会跳到更强(错误的)边界;(c)经过前一段训练后,更倾向于相似的边缘轮廓(Mortensen和Barrett 1998)©1995 Elsevier。
由于背景杂乱,与样条曲线垂直的条件密度(头部和肩部跟踪器质心的x坐标)可能有多个局部最大值。最后,图7.42c显示了在一段时间内跟踪几个人时条件密度的时间演变。
剪刀
活动轮廓允许用户大致指定感兴趣的边界,并让系统将轮廓演化到更精确的位置,同时跟踪其随时间的变化。然而,这种曲线演化的结果可能是不可预测的,可能需要额外的用户提示才能达到预期效果。
一种替代方法是让系统在用户绘制时实时优化轮廓(Mortensen 1999)。Mortensen和Barrett(1995)开发的智能剪刀系统正是这样做的。当用户绘制粗略轮廓(图7.43a中的白色曲线)时,系统会计算并绘制出更优的曲线,该曲线紧贴高对比度边缘(橙色曲线)。
为了计算最优曲线路径(活线),首先对图像进行预处理,将低成本与边缘(即相邻的水平、垂直和对角线,即N8邻域)关联起来,这些边缘可能是边界元素。他们的系统使用零交叉、梯度幅度和梯度方向的组合来计算这些成本。
接下来,当用户绘制一条粗略的曲线时,系统会使用迪杰斯特拉算法不断重新计算从起始种子点到当前鼠标位置之间的最低成本路径。
为了防止系统不可预测地跳跃,系统会在一段时间的不活动后“冻结”到目前为止的曲线(重置起始点)。为了防止导线跳到相邻的高对比度轮廓上,系统还会“学习”当前优化曲线下的强度分布,并利用这一点优先让导线沿着相同的(或相似的)边界移动(图7.43b-c)。
已提出几种扩展基本算法的方法,即使在原始形式下也能表现出色。莫滕森和巴雷特(1999)使用了滑板法,这是一种简单的分水岭区域分割方法,用于预先将图像分割成边界成为优化曲线路径候选的区域。这些区域边界被转换成一个更小的图,在该图中,节点位于三个或四个区域交汇的地方。然后在这一简化图上运行迪杰斯特拉算法,从而实现更快(且通常更稳定)的性能。智能剪刀的另一种扩展是采用概率框架,考虑边界当前的轨迹,从而形成一个名为JetStream的系统(普雷兹、布莱克和甘格内特2001)。
与在每个时间点重新计算最优曲线不同,可以通过简单地将当前鼠标位置“抓取”到最近的可能边界点来开发一个更简单的系统(Gleicher1995)。这些边界提取技术在图像切割中的应用
7.3.2水平集
基于参数曲线形式的主动轮廓,例如蛇形、B-蛇形和凝聚,其局限性在于,在曲线演化过程中改变其拓扑结构具有挑战性(McInerney和Terzopoulos 1999,2000)。此外,如果形状发生剧烈变化,可能还需要重新参数化曲线。
对于这些闭合轮廓,另一种表示方法是使用水平集,其中特征函数(或带符号距离(第3.3.3节))的零交叉点定义了曲线。水平集通过修改底层嵌入函数(即这个二维函数的另一个名称)φ(x;y),而不是曲线f(s),来适应和跟踪感兴趣的物体(Malladi、Sethian和Vemuri 1995;Sethian 1999;Sapiro 2001;Osher和Paragios 2003)。为了减少所需的计算量,只需在当前零交叉点周围更新一小段区域(边界),这导致了所谓的快速行进方法(Sethian 1999)。
一个演化方程的例子是卡塞勒斯提出的测地线活动轮廓,

图7.44测地线活动轮廓的水平集演化。嵌入函数φ根据底层表面的曲率更新,该曲率由边缘/速度函数g(I)调制,并且还根据g(I)的梯度进行更新,从而将其吸引到强边缘。
Kimmel和Sapiro(1997)以及Yezzi、Kichenassamy等人(1997),
· ▽φ, (7.38)
其中g(I)是蛇边势能的广义版本。为了直观地理解曲线的行为,假设嵌入函数φ是一条与曲线相距的带符号距离函数(图7.44),在这种情况下jφj = 1。方程(7.38)中的第一项使曲线沿其曲率方向移动,即在调制函数g(I)的影响下,它起到拉直曲线的作用。第二项使曲线沿着g(I)的梯度向下移动,促使曲线向g(I)的最小值迁移。
虽然这种水平集公式可以轻松改变拓扑结构,但它仍然容易受到局部最小值的影响,因为它是基于图像梯度等局部测量的。另一种方法是将问题重新表述为分割框架,在该框架中,能量衡量的是分割区域内外图像统计特性(如颜色、纹理、运动)的一致性(Cremers,Rousson和Deriche 2007;Rousson和Paragios 2008;Houhou,Thiran和Bresson 2008)。这些方法建立在Leclerc(1989)、Mumford和Shah(1989)以及Chan和Vese(2001)引入的早期基于能量的分割框架之上,相关内容详见Section4.3.2。
有关水平集及其应用的更多信息,请参见由Osher和Paragios编辑的论文集(2003年)以及关于变分和水平集方法在计算机视觉中的研讨会系列(Paragios,Faugeras等2005年)和关于尺度空间和变分方法在计算机视觉中的特刊(Paragios和Sgallari。

图7.45基于关键帧的转描(Agarwala,Hertzmann等人,2004)©2004
ACM: (a)原始画面;(b)转描轮廓;(c)重新上色的上衣;(d)转描手绘动画。
2009).
活动轮廓可用于多种物体跟踪应用(Blake和Isard 1998;Yilmaz、Javed和Shah 2006)。例如,它们可以用于追踪面部特征以实现性能驱动的动画(Terzopoulos和Waters 1990;Lee、Terzopoulos和Waters 1995;Parke和Waters 1996;Bregler、Covell和Slaney 1997)。它们还可以用于追踪头部和人物,如图7.42所示,以及移动车辆(Paragios和Deriche 2000)。其他应用包括医学图像分割,在计算机断层扫描中可以从一个切片到另一个切片追踪轮廓(Cootes和Taylor 2001),或随时间变化,如超声波扫描。
一个有趣的应用是转描技术,它利用跟踪轮廓来变形一组手绘动画(或修改或替换原始视频frames).14Agarwala,赫茨曼等人(2004)提出了一种基于跟踪选定关键帧的手绘B样条轮廓的系统,结合了几何和外观标准(图7.45)。他们还对之前的转描技术和基于图像的轮廓跟踪系统进行了出色的综述。
14这个术语来自于一种装置(arotoscope),它将真人电影的画面投射到醋酸纤维素下面,这样艺术家就可以直接在演员的形状上绘制动画。
477节介绍了将对象从一张照片剪切并粘贴到另一张照片中,参见第10.4节。
虽然边缘和一般曲线适合描述自然物体的轮廓,但人造世界充满了直线。检测和匹配这些直线在多种应用中都有用处,包括建筑建模、城市环境中的姿态估计以及打印文档布局的分析。
在本节中,我们介绍了一些从前一节计算的曲线中提取分段线性描述的技术。首先,我们介绍一些算法,用于将曲线近似为分段线性折线。接着,我们描述了霍夫变换,该变换可以将边缘点聚集成线段,即使在间隙和遮挡的情况下也能做到这一点。最后,我们描述了如何将具有共同消失点的三维线段聚类在一起。这些消失点可用于校准相机,并确定其相对于矩形场景的方向,如第11.1.1节所述。
正如我们在第7.2.2节中所见,将曲线描述为一系列二维位置xi=x(s)提供了一种通用表示方法,适用于匹配和进一步处理。然而,在许多应用中,更倾向于用更简单的表示来近似这种曲线,例如,作为分段线性折线或B样条曲线(Farin2002)。
多年来,人们开发了多种技术来实现这种近似,也称为线简化。其中最古老且简单的方法之一是由拉默(1972年)和道格拉斯与佩克(1973年)提出的,他们通过递归地将曲线在距离连接两个端点的直线(或当前粗略折线近似)最远的点处细分。赫舍伯格和斯诺因克(1992年)提供了一种更高效的实现方法,并引用了该领域的其他一些相关工作。
一旦计算出线简化,就可以用来近似原始曲线。如果需要更平滑的表示或可视化,可以使用近似或插值样条或曲线(第3.5.1节和第7.3.1节)(Szeliski和Ito1986;Bartels、Beatty和Barsky1987;Farin2002)。
虽然使用多段线进行曲线近似通常可以成功提取直线,但现实世界中的直线有时会被分解成不连通的组件或由许多直线组成

图7.47偏向霍夫变换:(a)在极坐标(r;θ)中参数化,其中i =(cos θi;sin θi)和ri = i·xi;(b)(r;θ)积累数组,显示了标记为红色、绿色和蓝色的三个边缘的投票结果。
共线线段。在许多情况下,将这些共线线段组合成延长线是可取的。在进一步处理阶段(第7.4.3节中描述),我们可以将这些线组合成具有共同消失点的集合
霍夫变换,以其原始发明者(Hough1962)命名,是一种著名的边缘“投票”技术,用于确定可能的线位置(Duda和Hart1972;Ballard 1981;Illingworth和Kittler1988)。在其最初的表述中(图7.46),每个边缘点都会对所有通过它的可能线条进行投票,而与高累加器或箱值相对应的线条则被检查以寻找潜在的线拟合。除非线上的点确实是孤立的,否则更好的方法是利用每个边缘点处的局部方向信息来投票给一个单独的累加器单元(图7.47),如下所述。一种混合策略,即每个边缘点投票
15Hough变换也可以推广到寻找其他几何特征,如圆(Ballard

在一些情况下,对于以估计方向为中心的多个可能的方向或位置对来说可能是可取的。
在我们投票支持线性假设之前,我们必须首先选择一个合适的表示。
图7.48(从图2.2a复制)显示了正常距离(d)参数化
一条直线。由于直线由边段组成,我们采用以下约定:直线的法线
与图像梯度J(x) =▽I(x)方向相同(即,具有相同的符号)的点
(7.19)为了获得直线的最小两个参数表示,我们将法向量转换为角度
θ = tan-1 ny /nx, (7.39)如图7.48所示。可能的(θ,d)值范围为[-180.,180.]×[-√2,√2],假设我们使用的是归一化的像素坐标(2.61),这些坐标位于[-1,1]内。每个轴上的区间数量取决于位置和方向估计的精度以及预期的线密度,并且最好通过在样本图像上进行一些测试运行来实验确定。
实现霍夫变换时有许多细节需要注意,包括在投票过程中使用边缘段长度或强度,在累加器数组中保存构成边的列表以便于后处理,以及可选地将不同“极性”的边合并为同一线段。这些细节最好通过编写实现并在样本数据上测试来解决。
对于线的二维极坐标(θ,d)表示法,另一种方法是使用完整的三维m=
(d)直线方程,投影到单位球上。虽然球可以参数化
使用球坐标(2.8),
=(cosθcosφ,sinθcosφ,sinφ), (7.40)
这并不能均匀地对球体进行采样,仍然需要使用三角学。
通过使用立方体映射,可以得到另一种表示方法,即将m投影到
单位立方体的表面(图7.49a)。计算三维向量的立方体坐标

图7.49线方程和消失点的立方体地图表示:(a)围绕单位球体的立方体地图;(b)将半立方体投影到三个子空间(Tuyte- laars、Van Gool和Proesmans1997)©1997 IEEE。
首先,找到m的最大(绝对值)分量,即m = ± max(jnxj,jny j,jdj),并用它来选择六个立方体面中的一个。将剩余的两个坐标除以m,并用这些坐标作为立方体面的索引。虽然这种方法避免了使用三角函数,但确实需要一些决策逻辑。
使用立方体图的一个优势,首先由图特拉尔斯、范古尔和普罗斯曼斯(1997)指出,是所有通过某一点的线都对应于立方体面上的线段,这在使用原始(全投票)霍夫变换时非常有用。在他们的研究中,他们表示直线方程为ax + b + y = 0,这并不对x和y轴进行对称处理。需要注意的是,如果我们通过忽略边缘方向(梯度符号)的极性来限制d≥0,就可以使用半立方体,仅需用三个立方体面即可表示,如图7.49b所示(图特拉尔斯、范古尔和普罗斯曼斯1997)。
基于RANSAC的线检测。霍夫变换的另一种替代方法是随机样本一致性(RANSAC)算法,该算法在第8.1.4节中详细描述。简而言之,RANSAC随机选择边对来形成一条线假设,然后测试有多少其他边落在这条线上。(如果边的方向足够准确,单个边就可以产生这个假设。)具有足够多内点(匹配的边)的线段随后被选为所需的线段。
RANSAC的一个优点是不需要累加器数组,因此算法可以更加节省空间,并且可能更少受到箱大小选择的影响。缺点是需要生成和测试的假设远多于通过在累加器数组中找到峰值所获得的假设。
自下而上的分组。另一种线段检测方法是将具有相似方向的边沿迭代地分组为有向矩形线支持区域(Burns,Han-

图7.50实际消失点:(a) architecture (Sinha,Steedly等人,2008),(b) furniture (Mi u k,Wildenauer和Ko eck,2008)©2008 IEEE,以及(c)校准模式(Zhang,2000)。
儿子,以及里斯曼1986)。然后可以使用统计分析来确定这些区域的有效性,如格罗蓬·冯·乔伊、雅库博维奇等人(2008)在LSD论文中所述。该算法非常快速,能够很好地区分线段和纹理,并因其性能和开源可用性而在实践中广泛使用。最近,已经开发出深度神经网络算法,可以同时提取线段及其连接点(黄、王等人2018;张、李等人2019;黄、秦等人2020;林、平特亚和范·格默特2020)。
一般来说,对于哪种线估计技术表现最佳并没有明确的共识。因此,仔细考虑问题并尝试几种方法(连续逼近、Hough和RANSAC)来确定最适合您应用的方法是个好主意。
在许多场景中,结构重要的线条因为三维空间中的平行性而具有相同的消失点。例如水平和垂直的建筑边缘、斑马线、铁路轨道、家具如桌子和衣柜的边缘,当然还有常见的校准图案(图7.50)。找到这些线条集合的共同消失点可以帮助精确定位它们在图像中的位置,在某些情况下,还可以帮助确定相机的内外方位(第11.1.1节)。
多年来,已经开发出大量技术来寻找消失点(Quan和Mohr 1989;Collins和Weiss 1990;Brillaut-O‘Mahoney 1991;McLean和Kotturi 1995;Becker和Bove1995;Shufelt1999;Tuytelaars,Van Gool,以及Proesmans 1997;Schaffalitzky和Zisserman 2000;Antone和Teller 2002;Rother 2002;Ko eck和Zhang

图7.51矩形检测:(a)室内走廊和(b)建筑物外部
分组立面(Ko eck和Zhang2005)©2005 Elsevier;基于(c)语法的识别
(Han和Zhu2005)©2005 IEEE;(d-f)使用平面扫描算法进行矩形匹配
(Mi u k、Wildenauer和Ko eck 2008)©2008 IEEE。
2012;Antunes和Barreto2013;Kluger、Ackermann等人2017;Zhou、Qi等人2019a)——请参阅一些较新的论文以获取更多参考文献和替代方法。
在本书的第一版(Szeliski2010,第4.3.3节)中,我介绍了一种基于线对投票潜在消失点位置的简单霍夫技术,随后进行稳健的最小二乘拟合阶段。虽然我的方法分为两个独立阶段,但通过交替分配线条到消失点和重新拟合消失点位置,可以取得更好的结果(Antone和Teller2002;Ko eck和Zhang2005;Pflugfelder2008)。检测单个消失点的结果也可以通过同时搜索相互正交的消失点对或三元组来提高
鲁棒性(Shufelt1999;Antone和Teller2002;Rother2002;Sinha、Steedy等人2008;Li、Kim等人2020)。图7.50展示了此类消失点检测算法的一些结果。还可以使用神经网络同时检测线段及其连接点(Zhang、Li等人2019),然后利用这些信息构建完整的3D线框模型(Zhou、Qi和Ma2019;Zhou、Qi等人2019b)。
矩形检测
一旦检测到一组相互正交的消失点,就可以在图像中搜索三维矩形结构(图7.51)。已经开发出多种技术来寻找这样的矩形,主要集中在建筑场景中。
(Ko eck和Zhang2005;Han
以及Ko eck
2008;Schindler,Krishnamurthy等人2008)。
检测到正交消失方向后,Ko eck和Zhang(2005)改进了拟合线方程
,寻找靠近线段交点的角点,然后通过校正相应区域并寻找大量水平和垂直边缘来验证矩形假设(图7.51a-b)。在后续工作中,Mi u k、Wilder和Ko eck(2008)使用马尔可夫随机场(MRF)来区分可能重叠的矩形假设。他们还使用平面扫描算法在不同视图之间
匹配
矩形(图7.51d-f)。
韩和朱(2005)提出了一种不同的方法,他们利用矩形形状的潜在语法和嵌套结构(矩形与消失点之间)来推断线段最可能分配给矩形的方式(图7.51c)。现在,使用规则、重复结构作为建模过程的一部分被称为整体3D重建(周、古川和马2019;周、古川等2020;平托雷、穆拉等2020),将在Section13.6.1on建模3D建筑中详细讨论。
图像分割的任务是找到“组合在一起”的像素组。在统计学和机器学习中,这个问题被称为聚类分析或更简单的聚类,是一个广泛研究的领域,有数百种不同的算法(Jain和Dubes 1988;Kaufman和Rousseeuw 1990;Jain、Duin和Mao 2000;Jain、Topchy等2004;Xu和Wunsch 2005)。我们已经在第5.2.1节讨论了一般向量空间聚类算法。聚类与分割的主要区别在于,前者通常忽略像素布局和邻域,而后者则高度依赖空间线索和约束。
在计算机视觉中,图像分割是最古老且研究最为广泛的问题之一(Brice和Fennema 1970;Pavlidis 1977;Riseman和Arbib 1977;Ohlander、Price和Reddy 1978;Rosenfeld和Davis 1979;Haralick和Shapiro 1985)。早期技术通常采用区域分割或合并的方法(Brice和Fennema 1970;Horowitz和Pavlidis 1976;Ohlander、Price和Reddy 1978;Pavlidis和Liow 1990),这些方法对应于分裂算法和聚类算法(Jain、Topchy等2004;Xu和Wunsch 2005),我们在此介绍
在第5.2.1节中进行了减少。最近的算法通常优化一些全局标准,例如区域内的一致性和区域间边界长度或不相似性(Leclerc1989;Mumford和Shah1989;Shi和Malik2000;Comaniciu和Meer2002;Felzenszwalb和Huttenlocher2004;Cremers、Rousson和Deriche2007;Pont-Tuset、Arbel ez等人2017)。
我们已经看到了使用图像形态学(第3.3.3节)、马尔可夫随机场(第4.3节)、活动轮廓(第7.3节)和水平集(第7.3.2节)进行图像分割的例子。在识别章节(第6.4节)中,我们研究了语义分割,其目标是将图像分解为具有语义标签的区域,如天空、草地以及个人和动物。在本节中,我们将回顾一些用于自下而上通用(非语义)图像分割的额外技术。这些技术包括基于区域分割和合并的算法、基于图的分割、概率聚合(第7.5.1节)、均值漂移模式查找(第7.5.2节)以及基于像素相似度度量的归一化切割分割(第7.5.3节)。由于许多这些算法已不再广泛使用,因此很多描述已经大大缩短,与本书第一版(Szeliski2010,第5章)中的描述相比,后者提供了更详细的说明。
由于图像分割领域的文献非常丰富,了解一些表现较好的算法的一个好方法是查看人类标注数据库上的实验比较(Arbel ez,Maire等2011;Pont-Tuset,Arbel ez等2017)。其中最著名的是伯克利分割数据
集和基准(Martin,Fowlkes
等2001),该数据集包含来自Corel图像数据集的1,000张图像,由30名人类受试者手动标注。Unnikrishnan、Pantofaru和Hebert(2007)提出了新的度量标准来比较分割算法,而Estrada和Jepson(2009)则比较了四种知名分割算法。Alpert、Galun等人(2007)还提供了一个更新的前景和背景分割数据库。
如第3.3.3节所述,分割灰度图像的最简单技术是选择一个阈值,然后计算连通分量。不幸的是,由于光照和对象内部统计变化,单个阈值很少足以处理整个图像。
区域分割(分裂聚类)。将图像逐步细分为更小的区域是计算机视觉中最古老的技术之一。Ohlander、Price和Reddy(1978)提出了一种这样的技术,首先计算整个图像的直方图,然后找到最佳阈值以分离直方图中的大峰值。这一过程会重复进行,直到区域变得相对均匀或低于某个特定大小。近年来的分割算法通常优化某些区域内相似性和区域间差异性的度量。这些内容将在第4.3.2节和第7.5.3节中讨论。
区域合并(凝聚聚类)。区域合并技术可以追溯到计算机视觉的早期。Brice和Fennema(1970)使用双网格来表示像素之间的边界,并根据相对边界长度和这些边界处可见边缘的强度来合并区域。
一种非常简单的基于像素的合并方法结合了平均颜色差异低于阈值或区域过小的相邻区域。将图像分割成这样的超像素(Mori,Ren等,2004),这些超像素没有语义意义,可以作为有用的预处理阶段,使立体匹配(Zitnick,Kang等,2004;Taguchi,Wilburn和Zitnick,2008)、光流(Zitnick,Jojic和Kang,2005;Brox,Bregler和Malik,2009)以及识别(Mori,Ren等,2004;Mori,2005;Gu,Lim等,2009;Lim,Arbel ez等,2009)等高级算法更快且更稳健。还可以通过从中粒度分割
(以四叉树表示)开始,然后允许合并和分裂操作来结合分割和合并(Horowitz和Pavlidis,1976;Pavlidis和Liow,1990)。
分水岭。一种与阈值处理相关的技术,因为它作用于灰度图像,即分水岭计算(Vincent和Soille 1991)。该技术将图像分割成多个集水区,这些区域是图像中的部分(可以解释为高度场或地形),雨水会流入同一个湖泊。计算这些区域的一种有效方法是从所有局部最小值开始淹没地形,并在不同演化组件相遇的地方标记山脊。整个算法可以使用像素优先队列和广度优先搜索来实现(Vincent和Soille1991).16
由于图像中很少有被较亮的脊线分隔的暗区,因此通常将分水岭分割应用于梯度幅值图像的平滑版本,这使得它也能用于彩色图像。作为替代方案,可以使用可导向滤波器(3.28–3.29)中的最大方向能量(Freeman和Adelson 1991)作为Arbel ez、Maire等人(2011)开发的方向分水岭变换的基础。这些技术最终会找到由可见(高梯度)边界分隔的平滑区域。由于这些边界通常是活动轮廓
通常跟随的目标,因此活动轮廓算法(Mortensen和Barrett 1999;Li、Sun等人2004)通常会预先计算这种分割,使用分水岭或
16相关算法可用于高效计算最大稳定极限区域(MSER)(第7.1.1节)(Nist r和Stew nius2008)。

图7.52基于图的合并分割(Felzenszwalb和Huttenlocher 2004)©2004斯普林格:(a)输入灰度图像成功分割为三个区域,尽管较小矩形内的变化大于中间边缘的变化;(b)输入灰度图像;(c)使用N8像素邻域的结果分割。
7.5.1基于图的分割
虽然许多合并算法只是简单地应用一个固定的规则来将像素和区域聚类在一起,但费尔岑斯瓦尔布和胡滕洛赫(2004)提出了一种使用区域间相对不相似性来确定哪些区域应该合并的合并算法;该算法能够证明优化全局聚类度量。他们首先使用像素间的不相似性度量w(e),例如测量N8邻域之间的强度差异。或者,他们可以使用科马尼丘和梅尔(2002)引入的联合特征空间距离,我们将在Sections7.5.2和7.5.3中讨论。图7.52显示了使用他们的技术分割的两个图像示例。
概率聚合
阿尔珀特、加伦等人(2007)开发了一种基于灰度相似性和纹理相似性的概率合并算法。区域Ri和Rj之间的灰度相似性基于与其他相邻区域的最小外部差异,该差异与平均强度差异进行比较,以计算两个区域应合并的可能性pij。合并过程采用层次化方式,受到代数多重网格技术(布兰特1986;布里格斯、亨森和麦考密克2000)的启发,并由阿尔珀特、加伦等人(2007)在其加权聚合分割(SWA)算法中使用过(沙伦、加伦等人2006)。图7.56显示了该算法生成的分割结果。
7.5.2平均偏移
均值移位和模式查找技术,如k-均值和高斯混合,将与每个像素相关的特征向量(例如,颜色和位置)建模为来自未知概率密度函数的样本,然后尝试在该分布中查找聚类(模式)。
考虑图7.53a所示的彩色图像。仅凭颜色,你如何分割这幅图像?图7.53b展示了L*u*v*空间中像素的分布,这相当于忽略空间位置的视觉算法所看到的情况。为了简化可视化,我们只考虑L*u*坐标,如图7.53c所示。你看到了多少明显的(拉长的)聚类?你会如何找到这些聚类?
我们在第5.2.2节中研究的k均值和高斯混合技术使用密度函数的参数模型来回答这个问题,即假设密度是由少量较简单的分布(例如高斯分布)的叠加而成,这些分布的位置(中心)和形状(协方差)可以被估计。而均值漂移则平滑分布并找到其峰值以及特征空间中对应每个峰值的区域。由于建模的是完整的密度,这种方法被称为非参数方法(Bishop 2006)。
均值漂移的关键在于一种高效地在高维数据分布中找到峰值的技术,而无需显式计算完整的函数(Fukunaga和Hostetler 1975;Cheng 1995;Comaniciu和Meer 2002)。再次考虑图7.53c中显示的数据点,可以认为这些数据是从某个概率密度函数中抽取的。如果我们能够计算出这个密度函数,如图7.53e所示,我们就能找到其主要峰值(模式),并识别出输入空间中达到相同峰值的区域属于同一区域。这与第7.5节描述的分水岭算法相反,后者是沿着山谷向下寻找吸引盆地的过程。
那么,第一个问题是如何根据稀疏样本集估计密度函数。最简单的方法之一是平滑数据,例如通过用宽度为h的固定核进行卷积,正如我们在Section4.1.1中所见,这是密度估计中的帕森窗口方法(Duda,Hart和Stork 2001,第4.3节;Bishop 2006,第2.5.1节)。一旦我们计算出f (x),如Figure7.53e所示,就可以使用梯度上升或其他优化技术找到其局部最大值。
这种方法的问题在于,对于更高维度的情况,评估整个搜索空间上的f (x)在计算上变得不可行。相反,均值漂移采用了一种优化文献中称为多次重启梯度下降的变体。从某个局部最大值的猜测点yk开始,该点可以是随机输入数据点xi,均值漂移计算f (x)在yk处的密度估计梯度,并取一个

图7.53均值偏移图像分割(Comaniciu和Meer2002)©2002 IEEE:
(a)输入彩色图像;(b)在L*u*v*空间中绘制的像素;(c) L*u*空间分布;(d)经过159次均值漂移处理后的聚类结果;(e)相应轨迹,峰值用红点标记。
朝这个方向迈出一步。有关如何高效地实现这一点的详细信息,可参见关于均值漂移的论文(Comaniciu和Meer2002;Paris和Durand2007)以及本书第一版(Szeliski2010,第5.3.2节)。
图7.53所示的颜色分割仅在确定最佳聚类时考虑像素颜色。因此,可能会将具有相同颜色的小孤立像素聚在一起,这可能不符合图像的语义分割。通常通过在颜色和位置的联合域中进行聚类可以获得更好的结果。在这种方法中,图像的空间坐标xs =(x,y),称为空间域,与颜色值xr,称为范围域,被连接起来,并在五维空间xj中应用均值漂移聚类。由于位置和颜色可能有不同的尺度,核函数分别调整,就像第3.3.2节讨论的双边滤波器核(3.34–3.37)一样。然而,均值漂移与双边滤波的区别在于,在均值漂移中,每个像素的空间坐标与其颜色值一起调整,使得该像素更快地向具有相似颜色的其他像素迁移,从而可以用于后续的聚类和分割。
均值漂移算法已应用于计算机视觉中的多个不同问题,包括人脸跟踪、二维形状提取和纹理分割(Comaniciu和Meer 2002),立体匹配(Wei和Quan 2004),非真实感渲染(第10.5.2节)(DeCarlo和Santella 2002),以及视频编辑(第10.4.5节)(Wang,Bhat等2005)。Paris和Durand(2007)对这些应用进行了很好的综述,同时提供了更高效地求解均值漂移方程和生成层次分割的技术。
7.5.3标准化切割
而自下而上的合并技术将区域聚合为连贯的整体,并进行平均移位
技术试图使用模式查找和归一化切割来寻找相似像素的簇
Shi和Malik(2000)提出的技术检查了邻近像素之间的亲缘关系(相似性),并试图分离由弱亲缘关系连接的组。
考虑图7.54a所示的简单图。A组中的像素都以高亲和力紧密相连,用粗红线表示;B组中的像素也是如此。这两组之间的连接,用细蓝线表示,要弱得多。一个归一化的切割线,用虚线表示,将它们分为两个簇。
两组A和B之间的切割定义为所有权重被切割的总和,其中两个像素(或区域)i和j之间的权重衡量它们的相似度。然而,使用最小切割作为分割标准并不能产生合理的聚类,因为最小切割通常涉及隔离单个像素。

图7.54样本加权图及其归一化切割:(a)小样本图及其最小归一化切割;(b)该图关联和切割的表格形式。关联和切割条目是通过相关权重矩阵W的面积之和计算得出的。通过行或列求和对表格条目进行归一化,得到归一化的关联和切割Nassoc和Ncut。
更好的分割度量是归一化切割,定义为
N切割
(7.41)
其中assoc(A,A)=εi∈A;j∈A wij表示A内的关联(所有权重之和)
聚类和关联(A,V)=关联(A,A)+切割(A,B)是与节点A中的所有权重之和。图7.54b展示了如何将切割和关联视为权重矩阵W = [wij ]中的面积之和,其中矩阵的条目已排列为节点A在前,节点B在后。将这些面积除以相应的行和(图7.54b最右列)得到归一化的切割和关联值。这些归一化值更好地反映了特定分割的适应性,因为它们寻找的是相对于特定区域内部和外部所有边而言较弱的边集合。
不幸的是,计算最优归一化切割是NP完全问题。因此,Shi和Malik(2000)建议使用归一化亲和矩阵的广义特征值分析来计算节点到组的实值分配(Weiss1999),具体细节参见归一化切割论文和(Szeliski2010,第5.4节)。由于这些特征向量可以解释为弹簧-质量系统中的大振动模式,归一化切割是一种用于图像分割的谱方法。在计算出实值特征向量后,与正负特征向量值相对应的变量被关联到两个切割组件。这一过程可以进一步重复,以层次方式细分图像,如图7.55所示。
Shi和Malik(2000)提出的原始算法使用了空间位置和图像

图7.55归一化切割分割(Shi和Malik2000)©2000 IEEE:输入图像和归一化切割算法返回的组件。
特征差异用于计算像素间的相似度。在后续的研究中,Malik、Belongie等人(2001)寻找像素i和j之间的中间轮廓,定义中间轮廓权重,然后将这些权重与基于纹理块的纹理相似度度量相乘。他们随后使用基于局部像素特征的初始过度分割,以区域为基础重新估计中间轮廓和纹理统计。图7.56展示了该改进算法在多个测试图像上的运行结果。
由于需要求解大型稀疏特征值问题,归一化切割可能相当缓慢。Sharon、Galun等人(2006)提出了一种加速归一化切割计算的方法,该方法受到代数多重网格(Brandt1986;Briggs,Henson,and McCormick2000)的启发。
图7.56展示了加权聚合(SWA)产生的分割示例,以及Alpert、Galun等人(2007)提出的最新概率自下而上的合并算法。在更近期的研究中,Pont-Tuset、Arbel ez等人(2017)加速了归一化切割,并将其扩展到多个尺度,从而在伯克利分割
数据集上取得了最先进的结果,同时在VOC和COCO数据集上也实现了对象建议的最先进成果。
关于特征检测、描述和匹配的开创性论文之一是Lowe(2004)。Schmid、Mohr和Bauckhage(2000)、Mikolajczyk和Schmid(2005)、Mikolajczyk、Tuytelaars等人对这些技术进行了全面的调查和评估。

图7.56比较分割结果(Alpert,Galun等人,2007)©2007 IEEE。“我们的方法”指的是Alpert等人开发的概率自下而上的合并算法。
al.(2005)和Tuytelaars和Mikolajczyk(2008),而Shi和Tomasi(1994)和Triggs
(2004)也提供了很好的评论。
在特征检测器领域(Mikolajczyk,Tuytelaars等2005),除了经典的Frstner-Harris(F rstner1986;Harris
和Stephens1988
)和高斯差分(Lindeberg1993,1998b;Lowe2004)方法外,最大稳定极值区域(MSERs)也被广泛用于需要仿射不变性的应用(Matas,Chum等2004;Nist r和Stew nius2008)。最近的兴趣点检测器由Xiao和Shah(2003)、Koethe
(2003)、Carneiro和Jepson(2005)、Kenney,Zuliani和Manjunath(2005)、Bay,Ess等(2008)、Platel,Balmachnova等(2006)以及Rosten,Porter和Drummond(2010)讨论,基于线匹配的技术(Zoghlami,Faugeras和Deriche1997;Bartoli,Coquerelle和Sturm2004)和地区检测(Kadir,Zisserman和Brady2004;Matas,Chum等2004;Tuytelaars和Van Gool2004;Corso和Hager 2005)也是如此。三篇关于基于DNN的特征检测器的优秀综述论文分别由Balntas,Lenc等(2020)、Barroso-Laguna,Riba等(2019)和Tian,Balntas等(2020)撰写。
米科拉伊奇克和施密德(2005)调查并比较了多种局部特征描述符(及匹配启发式方法)。该领域的较新出版物包括范德韦杰尔和施密德(2006)、阿卜杜勒-哈基姆和法拉格(2006)、温德和布朗(2007)以及华、布朗和温德(2007)的著作,还有巴尔恩塔斯、伦茨等人(2020)和金、米什金等人(2021)的最新评估。高效匹配特征的技术包括k-d树(贝斯和洛厄1999;洛厄2004;穆贾和洛厄2009)、金字塔匹配核(格劳曼和达雷尔2005)、度量(词汇)树(尼斯特和斯图尼乌斯2006),
多种多维哈希技术(Shakhnarovich、Viola和Darrell 2003;Torralba、Weiss和Fergus 2008;Weiss、Torralba和Fergus 2008;Kulis和Grauman 2009;Raginsky和Lazebnik 2009),以及产品量化(J gou、Douze和Schmid 2010;Johnson、Douze和J
gou 2021)。关于大规模系统用于
实例检索的综述,可参考Zheng、Yang和Tian(2018)。
关于特征检测和跟踪的经典参考文献是Shi和Tomasi(1994)。该领域的最新研究集中在为特定特征学习更好的匹配函数(Avidan2001;Jurie和Dhome2002;Williams、Blake和Cipolla2003;Lepetit和Fua 2005;Lepetit、Pilet和Fua2006;Hinterstoisser、Benhimane等人2008;Rogez、Rihan等人。
Al.2008;zuysal,Calonder等人2010)。
一个被广泛引用和使用的边缘检测器是由Canny(1986)开发的。关于替代边缘检测器以及实验比较的研究,可以在Nalwa和Binford(1986)、Nalwa(1987)、Deriche(1987)、Freeman和Adelson(1991)、Nalwa(1993)、Heath、Sarkar等人(1998)、Crane(1997)、Ritter和Wilson(2000)、Bowyer、Kranenburg和Dougherty(2001)、Arbel ez、Maire等人(2011)以及Pont
-Tuset、Arbel ez等人(2017
)的出版物中找到。边缘检测中的尺度选择问题由Elder和Zucker(1998)进行了很好的处理,而颜色和纹理边缘检测的方法则可以在Ruzon和Tomasi(2001)、Martin、Fowlkes和Malik(2004)以及Gevers、van de Weijer和Stokman(2006)的著作中找到。边缘检测器还与区域分割技术结合使用,以进一步提高对语义显著边界检测的效果(Maire、Arbel ez等人2008;Arbel ez、Maire等人2011;Xiaofeng和Bo2012;Pont-Tuset、Arbel
ez等人2017)。连接成轮廓的边缘可以平滑和操作以
产生艺术效果(Lowe1989;Finkelstein和Salesin1994;Taubin1995),并用于识别(Belongie、Malik和Puzicha2002;Tek和Kimia2003;Sebastian和Kimia2005)。
活动轮廓的主题有着悠久的历史,始于关于蛇和其他能量最小化变分方法的开创性工作(Kass、Witkin和Terzopoulos 1988;Cootes、Cooper等1995;Blake和Isard 1998),继而发展到智能剪刀技术(Mortensen和Barrett 1995,1999;P rez、Blake和Gangnet 2001),最终演变为水平集方法(Malladi、Sethian和Vemuri 1995;Caselles、Kimmel和Sapiro 1997
;Sethi an 1999;Paragios和Deriche 2000;Sapiro 2001;Osher和Paragios 2003;Paragios、Faugeras等2005;Cremers、Rousson和Deriche 2007;Rousson和Paragios 2008;Paragios和Sgallari 2009),这些方法目前是最广泛使用的活动轮廓方法。
Burns、Hanson和Riseman(1986)撰写了一篇关于图像中直线提取的早期、备受推崇的论文。Grompone von Gioi、Jakubowicz等人(2008)扩展了他们的自下而上的线支持区域概念,构建了流行的LSD线段。
检测器。关于消失点检测的文献非常丰富且仍在不断发展中(Quan和Mohr 1989;Collins和Weiss 1990;Brillaut-O‘Mahoney 1991;McLean和Kotturi 1995;Becker和Bove 1995;Shufelt 1999;Tuytelaars、Van Gool和Proesmans 1997;Schaffalitzky和Zisserman 2000;Antone和Teller 2002;Rother 2002;Ko eck和Zhan
2005;Denis、Elder和Estrada2008;Pflugfelder2008;Tardif2009;Bazin,Seo等2012;Antunes和Barreto 2013;Zhou、Qi等2019a)。同时,线段和节点检测技术也已开发出来(Huang、Wang等2018;Zhang、Li等2019)。
图像分割这一主题与聚类技术密切相关,这在许多专著和综述文章中都有论述(Jain和Dubes 1988;Kaufman和Rousseeuw 1990;Jain、Duin和Mao 2000;Jain、Topchy等2004)。一些早期的分割技术包括Brice和Fennema(1970)、Pavlidis(1977)、Rise-man和Arbib(1977)、Ohlander、Price和Reddy(1978)、Rosenfeld和Davis(1979)以及Haralick和Shapiro(1985)所描述的技术,而较新的技术则由Leclerc(1989)、Mumford和Shah(1989)、Shi和Malik(2000)以及Felzenszwalb和Hutten- locher(2004)开发。
Arbel ez、Maire等人
2011)和Pont-Tuset、Arbel ez等
人(2017)对自动分割技术进行了很好的综述,并在Berkeley分割数据集和基准测试(Martin、Fowlkes等人,2001)上比较了它们的性能。17其他比较论文和数据库包括Unnikrishnan、Pantofaru和Hebert(2007)、Alpert、Galun等人(2007)以及Estrada和Jepson(2009)。
基于局部像素相似性的图像分割技术结合聚合或分裂方法包括分水岭(Vincent和Soille1991;Beare2006;Arbel ez,Maire等人2011),区域分裂(Ohlander,Price,and Reddy1978
),区域合并(Brice和Fennema1970;Pavlidis和Liow1990;Jain,Topchy等人2004),以及基于图和概率的多尺度方法(Felzenszwalb和Huttenlocher2004;Alpert,Galun等人2007)。
均值移位算法,用于在像素的密度函数表示中找到模式(峰值),由Comaniciu和Meer(2002)以及Paris和Durand(2007)提出。高斯混合参数化也可用于表示和分割此类像素密度(Bishop2006;Ma,Derksen等2007)。
关于图像分割的谱(特征值)方法的开创性工作是石和马利克(2000)提出的归一化切割算法。相关研究还包括韦斯(1999)、梅尔和石(2000)、梅尔和石(2001)、马利克、贝隆
吉等人(2001)、吴、乔丹和韦斯(2001)、余和石(2003)、库尔、布尼茨和石(2005)、沙伦、加伦等人(2006)、托利弗和米勒(2006)以及王和奥利恩斯(2010)。


























 619
619

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








