理解神经网络中的Dropout

dropout是指在深度学习网络的训练过程中，对于神经网络单元，按照一定的概率将其暂时从网络中丢弃。注意是暂时，对于随机梯度下降来说，由于是随机丢弃，故而每一个mini-batch都在训练不同的网络。

过拟合是深度神经网（DNN）中的一个常见问题：模型只学会在训练集上分类，这些年提出的许多过拟合问题的解决方案，其中dropout具有简单性而且效果也非常良好。

算法概述

我们知道如果要训练一个大型的网络，而训练数据很少的话，那么很容易引起过拟合，一般情况我们会想到用正则化、或者减小网络规模。然而Hinton在2012年文献：《Improving neural networks by preventing co-adaptation of feature detectors》提出了，在每次训练的时候，随机让一半的特征检测器停过工作，这样可以提高网络的泛化能力，Hinton又把它称之为dropout。

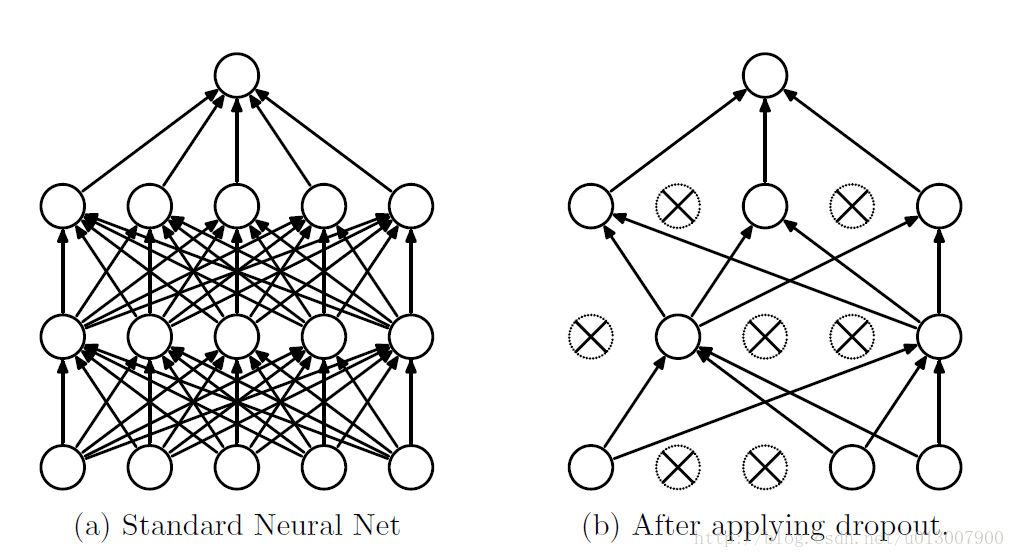
第一种理解方式是，在每次训练的时候使用dropout，每个神经元有百分之50的概率被移除，这样可以使得一个神经元的训练不依赖于另外一个神经元，同样也就使得特征之间的协同作用被减弱。Hinton认为，过拟合可以通过阻止某些特征的协同作用来缓解。

第二种理解方式是，我们可以把dropout当做一种多模型效果平均的方式。对于减少测试集中的错误，我们可以将多个不同神经网络的预测结果取平均，而因为dropout的随机性，我们每次dropout后，网络模型都可以看成是一个不同结构的神经网络，而此时要训练的参数数目却是不变的，这就解脱了训练多个独立的不同神经网络的时耗问题。在测试输出的时候，将输出权重除以二，从而达到类似平均的效果。

需要注意的是如果采用dropout，训练时间大大延长，但是对测试阶段没影响。

带dropout的训练过程

而为了达到ensemble的特性，有了dropout后，神经网络的训练和预测就会发生一些变化。在这里使用的是dropout以$p$的概率舍弃神经元

训练层面

对应的公式变化如下如下：

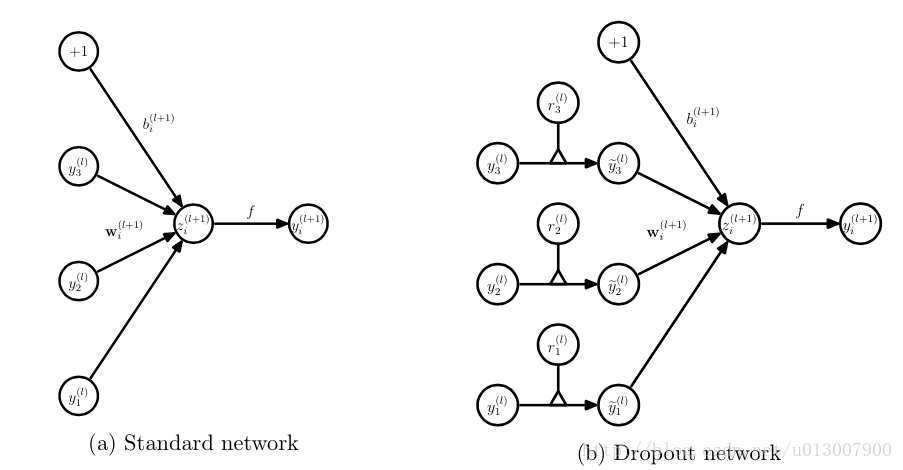
没有dropout的神经网络

$$z_i^{l+1} = w_i^{l+1}y^l+b_i^{l+1}\\ y_i^{l+1} = f(z_i^{l+1})$$

有dropout的神经网络

$$r_j^j～ Bernoulli(p)\\ {\tilde y^l} = r^l*y^l\\ z_i^{l+1} = w_i^{l+1}{\tilde y^l}+b_i^{l+1}\\ y_i^{l+1} = f(z_i^{l+1})$$

无可避免的，训练网络的每个单元要添加一道概率流程。

测试层面

预测的时候，每一个单元的参数要预乘以p。

除此之外还有一种方式是，在预测阶段不变，而训练阶段改变。

Inverted Dropout的比例因子是${1\over 1-p}$

$$r_j^j～ Bernoulli(p)\\ {\tilde y^l} = r^l*y^l\\ z_i^{l+1} = w_i^{l+1}{\tilde y^l}+b_i^{l+1}\\ y_i^{l+1} = {1\over 1-p}f(z_i^{l+1})$$

关于这个比例我查了不少资料，前面的是论文的结论；后面是keras源码中dropout的实现。有博客写的公式不一致，我写了一个我觉得是对的版本。

Dropout与其它正则化

Dropout通常使用L2归一化以及其他参数约束技术。正则化有助于保持较小的模型参数值。

$$w = w - \eta({\partial f(W;x)\over \partial w}+\lambda w)$$

使用Inverted Dropout后，上述等式变为：

$$w = w - \eta({1\over 1-p}{\partial f(W;x)\over \partial w}+\lambda w)$$

可以看出使用Inverted Dropout，学习率是由因子$q = 1-p$进行缩放 。由于q在[0,1]之间，$η$和q之间的比例变化：

$$r(q) = {\eta\over q}\in [\eta=\lim_{q\rightarrow 1}r(q), +\infty = \lim_{q\rightarrow 0}r(q)]$$

参考文献将q称为推动因素，因为其能增强学习速率，将r(q)称为有效的学习速率。

有效学习速率相对于所选的学习速率而言更高：基于此约束参数值的规一化可以帮助简化学习速率选择过程。

---

• Improving neural networks by preventing co-adaptation of feature detectors
• Improving Neural Networks with Dropout
• Dropout: A Simple Way to Prevent Neural Networks from Overtting
• ImageNet Classification with Deep Convolutional