矩阵变换基础方式包括:平移、旋转、缩放、对称(或者叫做镜像)、错切、投影。
复合变换的总结:
- 刚体变换:平移+旋转,只改变物体位置,不改变物体形状。
- 仿射变换:改变物体位置和形状,但是原来平行的边依然平行,也就是‘平直性’。
- 透视变换(也称投影变换):彻底改变物体位置和形状。
未知参数量:
- 仿射变换的方程组有6个未知数,所以要求解就需要找到3组映射点,三个点刚好确定一个平面(即使数组长度为4也仅取前3个点作为基准点)。
- 透视投影变换的方程组有8个未知数,所以要求解就需要找到4组映射点,四个点就刚好确定了一个三维空间(即使数组长度为5也仅取前4个点作为基准点)。
目录
1.矩阵变换的简单理解
我们从理论上理解了图形学中图形的变换过程,具体可以理解为如果要对一个图形A进行变换,那么存在图形A所处的相同原点的仿射空间SpaceA(或者说仿射空间SpaceA中原点处存在一个图形A),这时候我们暂时忽略图形A,只考虑SpaceA经过各种变换最终变换成另一个仿射空间SpaceB(或者说变换后的仿射空间SpaceA与另一个仿射空间SpaceB重合),因为仿射空间SpaceA变换后可能被伸缩或者被旋转同时又移动了,那么仿射空间SpaceA中的图形A同时跟着被变换成了另外的样子,如下图:

举个例子:
想像一下,假设把你自己当作一个“图形”,这时候出现一个任务,就是让躺在床上的你从家里出发去公司坐在办公椅上上班写代码,你应该怎么做呢,首先你要起床(从平躺的向量变成竖着的向量,这就经历了一个人体旋转的过程),然后出发,经过一条长长的街道xxx路(从xxx路的起点路口到xxx路的终点路口,这就经历了一个人体平移的过程),然后拐弯进入yyy路并且继续行走(这就经历了人体旋转加人体平移两个过程),然后进入公司走到办公椅前坐下(从竖着站立状态变成坐下的坐立状态,这可以人为人体进行了形变缩放)。
这么一看,我们对于变换的理解就可以分解为旋转、平移、缩放三个过程。
2.图像变换的方式
2.1 旋转
矩阵操作仿射坐标系旋转,还是老办法,建立单位圆进行逆时针旋转θ角(三角函数中规定逆时针旋转为正角)的旋转矩阵辅助推导,如下图:

我们通过矩阵T_rotate旋转变换仿射坐标系xoy到x1oy1,矩阵T_rotate的推导也是通过建立线性方程组解方程得到T_rotate的未知数。那么仿射坐标系所“容纳”的原点图形也就跟着变换了。因为旋转变换不需要额外扩充成齐次坐标表示也能进行变换,所以我们忽略“平移维度”。
2.1.1 扩展到三维空间
三维下的旋转就会复杂一些,不同于二维坐标系旋转只能绕着那个不存在的Z轴正反旋转(或者说我们在纸上画一个XYZ三维仿射坐标系,但是Z轴垂直于纸面我们看不到,那么以XY为坐标轴的二维坐标系就只能绕着Z轴旋转,因为我们习惯性把旋转角按逆时针标记(三角函数中规定逆时针旋转为正角),这个前面我们讨论三角函数说过了,所以顺时针旋转我们也能通过转换得到逆时针旋转的θ角度值,那么也就是说XY二维坐标系的旋转就是绕着Z轴逆时针旋转),此时三维XYZ坐标系的旋转就变成了XY绕着Z逆时针旋转,XZ绕着Y逆时针旋转,YZ绕着X逆时针旋转,现在我们依次来推导:
(1)XY绕Z轴逆时针旋转,如下图:

(2)XZ绕Y轴逆时针旋转,这个时候就要注意了,因为图形学有左右手坐标系之分,简单来说就是Z轴是向内还是向外的区别,我们可以观察得到unity的坐标系是左手坐标系,也就是Z轴向内,如下图:

那么我们建立矩阵和已知量的推导就变成如下图:

(3)YZ绕X轴逆时针旋转

2.2 缩放
矩阵操作仿射坐标系缩放,建立辅助单位圆,如下图:

上面我们首先推导了标准缩放,也就是xy缩放比例K相同,接下来缩放比例不同x缩放m/y缩放n,依旧是通过建立矩阵T_scale以及转换成线性方程组就很容易得到矩阵T_scale了。
扩展到三维空间

2.3 平移
矩阵操作仿射坐标系平移,特殊情况来了!前面我们讲过仿射坐标系平移是不能直接进行线性变换的,而需要扩充平移维度进行辅助计算,如下图:

同样的,因为二维平移只有xy轴两个方向,我们建立仿射坐标系观察,同时扩充“平移维度”,建立矩阵T_translate和线性方程组,就能得到我们需要的平移矩阵T_translate。
前面我们推了二维情况下仿射坐标系旋转,缩放,平移的变换矩阵T_rotate,T_scale,T_translate,但是三个矩阵太不规范了,有的是2x2有的是3x3,有的使用了齐次坐标,有的又只使用了普通坐标,这对我们程序中进行计算是非常不友好的。之前我们说了平移变换是通过扩充“平移维度”来处理的,并不影响“旋转维度”和“缩放维度”,同时GPU设计的重要指标之一就是极快速处理4x4及以下的矩阵计算,所以我们通过将T_rotate和T_scale扩充维度到T_translate的行列数,用来统一传入GPU进行处理。
扩充方式如下图:

扩展到三维空间

2.4 对称
对称变换也称为反射变化或镜像变换,变换后的图形是原图形关于某一轴线或原点的镜像。





2.5 错切
2.5.1 二维错切
水平方向


垂直方向


2.5.2 三维错切
这里要介绍一下仿射变换的一个特点,就是“平直性”,因为前面我们理解仿射变换是一个线性变换加上一个平移,线性这个性质就保证了直线变换后还是直线,所以仿射变换,变换后的图形,是直线边的还是直线边。
切变是一种特殊的“平直性”变换,简单来说就是矩形变为平行四边形,长方体变为平行六面体,如下图:

上面展示了长方体沿着X轴进行切变的示意图,从图中我们可以看出长方体沿X轴两边经过非单位1的等比例平移得到平行四边形,然后”牵引“整个长方体”扭曲“成平行六面体,所以切变矩阵的变换参数肯定存在有多个变动的缩放因子K。事实上,数学上规定n维仿射坐标系下的切变变换是取出一个切变方向坐标轴,然后将其他轴乘以切变因子再加到切变方向轴上。既然有了概念和定义,那我们就很容易推导了,如下图:

沿着X轴切变的推导过程还是很简单的,那么我们继续进行Y轴切边和Z轴切边推导,如下图:

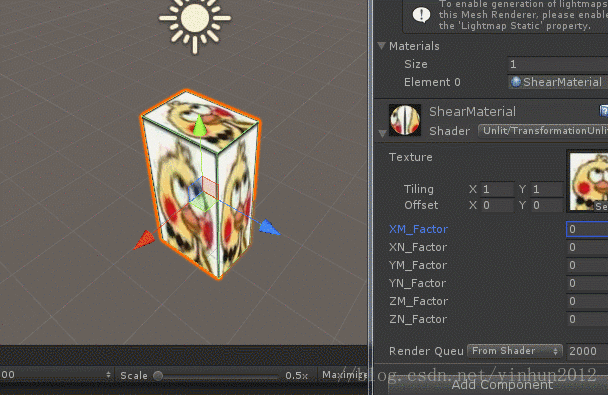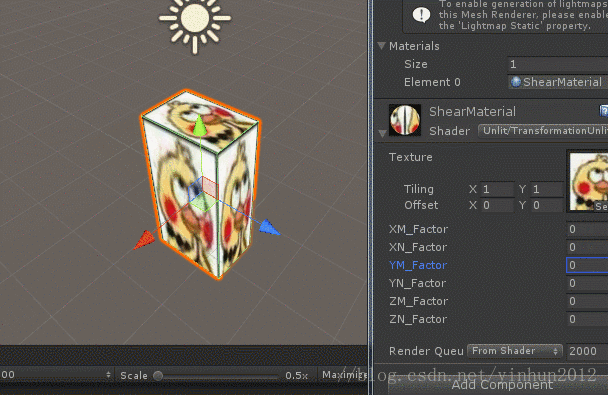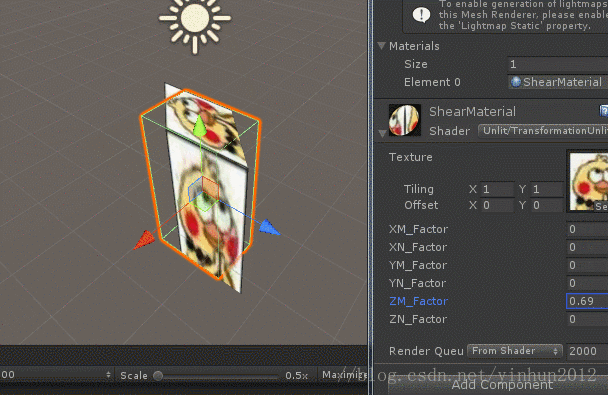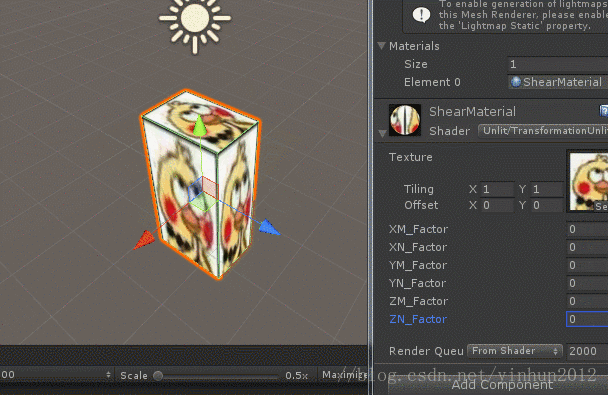
2.6 透视变换 (也称投影变换)
简单说,透视变换(也称投影变换)彻底改变目标的形状。
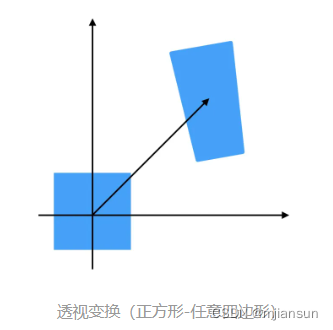




这个S是使用了齐次坐标的因素,可以表示透视关系。
3. 复合变换
假设我们有两个2x2的矩阵T1,T2来变换一个2x1的矩阵V(2x1的矩阵也就是一个二维向量),按照平常方法我们肯定就是先使用T1*V变换得到V1,然后再使用T2*V1变换得到V2,整个过程我们记为T2*(T1*V)。我们希望优化中间环节,尽量少的直接将V带入运算,希望变换成(T2*T1)*V,先将T2*T1得到矩阵T3,然后将T3*V变换得到V2,此时我们的问题就变成T2*T1得到的矩阵T3是否起到了T1、T2分别变换V相同的作用。
接下来就需要解决T2*(T1*V)与(T2*T1)*V是否相等的问题
我们知道矩阵A*矩阵B的规则就是矩阵A的行m与矩阵B的列n的元素分别相乘再相加最终得到的元素放置于结果矩阵C的m行n列中,那么上面的问题矩阵T1*V得到的V1再使用T2*V1得到的结果和T2*T1得到T3*V的结果相同,因为这种矩阵乘法的计算规律在独立出每个行列计算后得到单个元素的分解式符合乘法分配律(c*(a+b) = c*a + c*b)运算然后拆分组合成另外的乘法分配律的组合体,这时候我们必须通过实际运算来观察,因为红色语言的描叙都过于复杂到无法直接心算,如下图:

最后的乘法分配组合经过分解拆分继续组合成乘法分配律组合体。
结论:
T_rotate*(T_translate*(T_scale*Vector))等价于
T_all*Vector
其中T_all = T_rotate*(T_translate*T_scale))
4. 变换矩阵总结
4.1 示意图总结
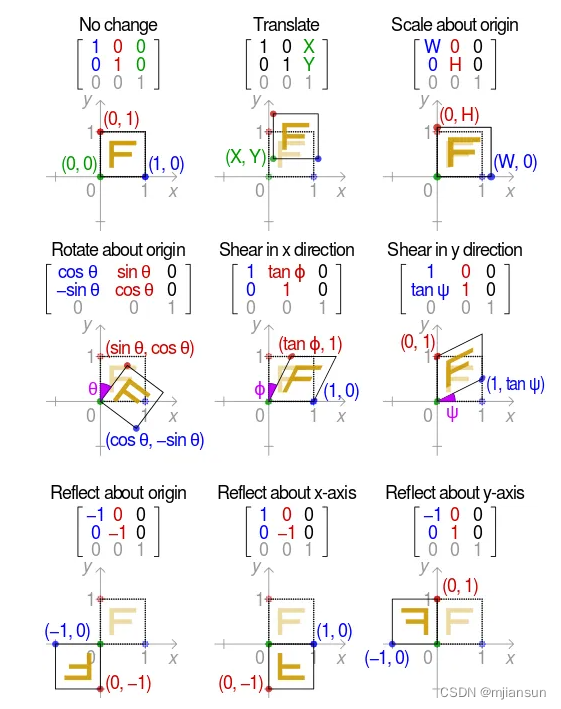
4.2 变换区域的含义

参考
(356条消息) 线性代数:矩阵变换图形(二维平移缩放旋转)_二维平移矩阵_羊羊2035的博客-CSDN博客
(349条消息) 线性代数:矩阵变换图形(三维平移缩放旋转)_三维几何缩放矩阵_羊羊2035的博客-CSDN博客








 文章详细介绍了矩阵变换的基础,包括平移、旋转、缩放、对称、错切和透视变换。在二维和三维空间中,这些变换通过矩阵运算来实现,例如旋转可以通过旋转矩阵完成,平移需要借助齐次坐标。文章还探讨了复合变换的概念,如刚体变换、仿射变换和透视变换,并解释了如何通过矩阵的乘法组合来简化变换过程。
文章详细介绍了矩阵变换的基础,包括平移、旋转、缩放、对称、错切和透视变换。在二维和三维空间中,这些变换通过矩阵运算来实现,例如旋转可以通过旋转矩阵完成,平移需要借助齐次坐标。文章还探讨了复合变换的概念,如刚体变换、仿射变换和透视变换,并解释了如何通过矩阵的乘法组合来简化变换过程。

















 2348
2348

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








