The problem of overfitting
Linear Regression 和 Logistic Regression 可以解决很多的现实问题,但是有时它们也会遇到一些问题,那就是Overfitting(过拟合)的问题,可能会导致它们的效果变差。
解决过拟合问题的一个可行途径是 Regularization(正规化)的技术,它可以改善或减少过度拟合的问题,从而使算法的表现更好(更接近现实中的表现)。
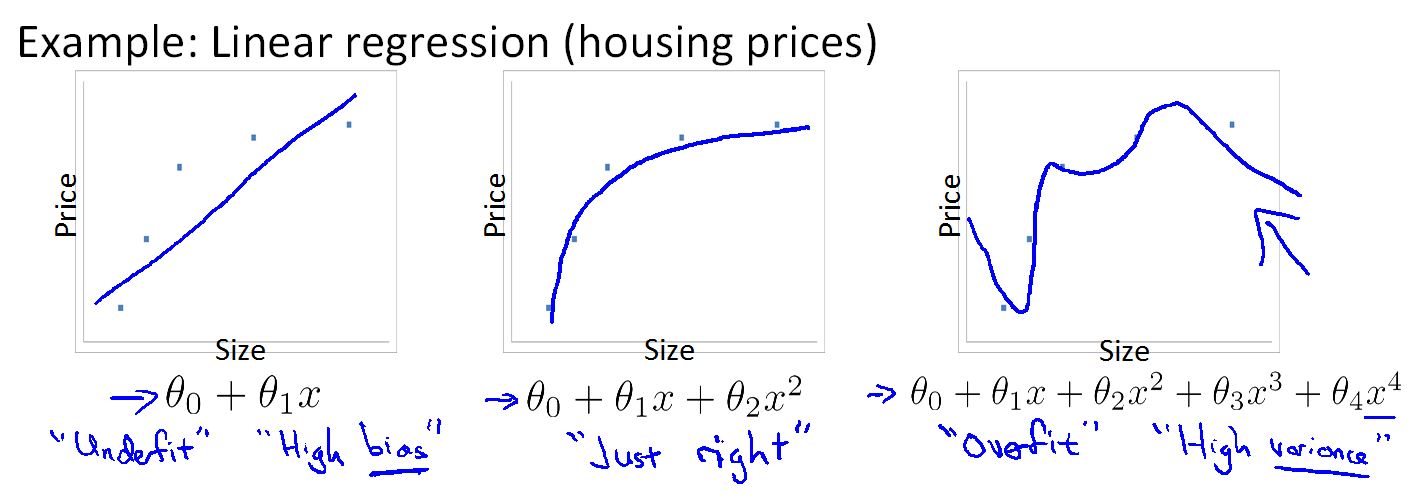
先说明什么是过拟合问题:(用预测房价的例子)
在上面我们训练了三个hypothesis 从低次(左)到高次(右)
第一个图说明:数据中表现是租房价格随着面积趋于稳定(越往右越平缓),但拟合曲线却不这么认为,曲线表明房价和面积成正比。所以拟合曲线不能很好的表现数据。这个问题是欠拟合问题(underfitting)也可称为高偏差(high bias)问题,意思是它没有很好的拟合训练数据,拟合曲线对数据有非常大的偏差。
第三个图说明:拟合曲线很好的拟合了数据,这个样本只有四个数据,用一个四次多项式,我们可以很好的拟合数据(可以说没有任何的偏差,拟合曲线对所有的样本都进行了正确的预测)但我们比不认为它是一个好模型。这个问题是过拟合问题(overfitting)也可称为高方差(high variance)问题,这会面临函数太过庞大的问题。
第二个图说明:正好合适。
过拟合就是说:训练的方程总数能很好的拟合训练数据,代价函数J(θ)几乎为零。它对训练集的拟合太好了,以至于它在新的数据上泛化能力不足,指的是一个假设模型能够应用到新样本的能力不足。
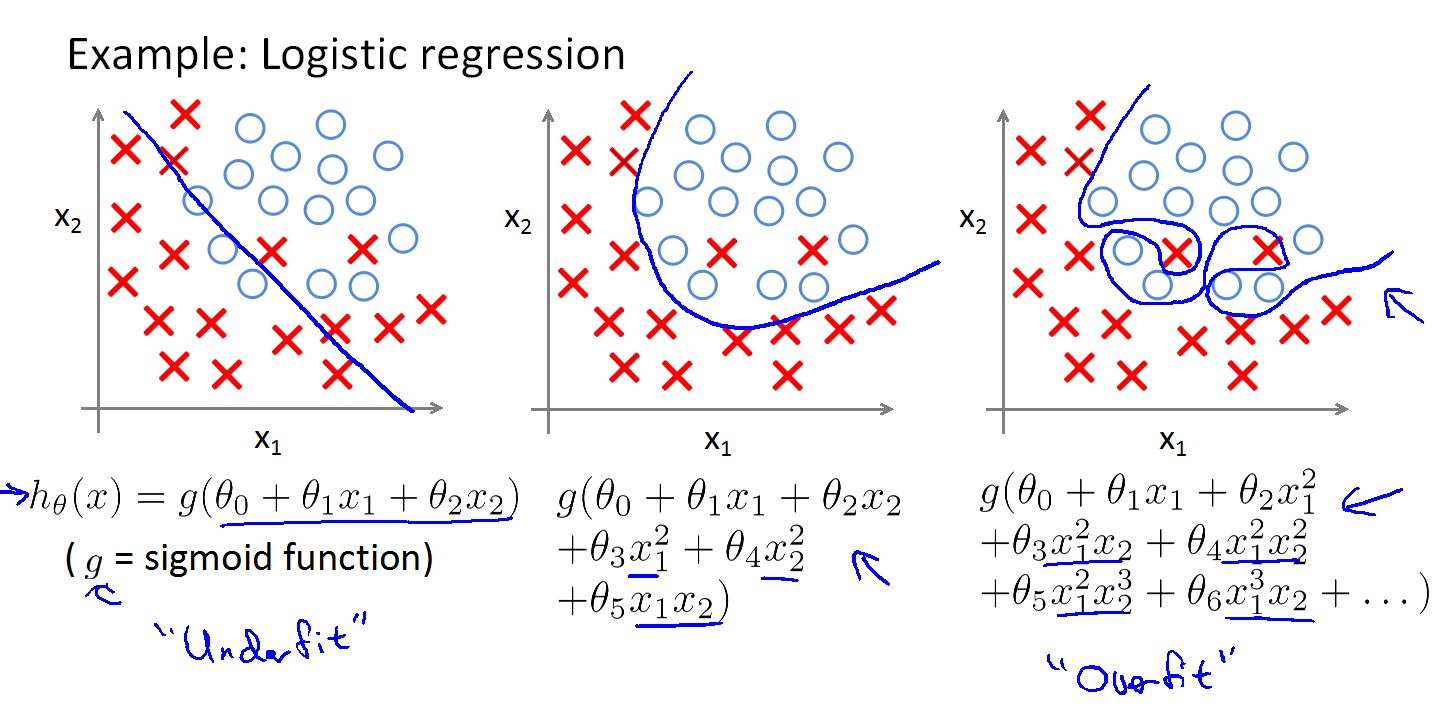
在逻辑回归中我们也面临这样的问题,可以看到第一个图是欠拟合,第三个图是过拟合,在只有很少参数的情况下,参数少于三个时,我们可以通过画图来识别欠拟合问题和过拟合问题。
避免overfitting的办法有两个:
1.减少选取的变量数量:用人工选取特征(效率低),用算法选取特征.缺点是:在舍弃特征的同时,也把其中包含的信息一并舍弃。
2.应用regularization 技术。
Cost Function
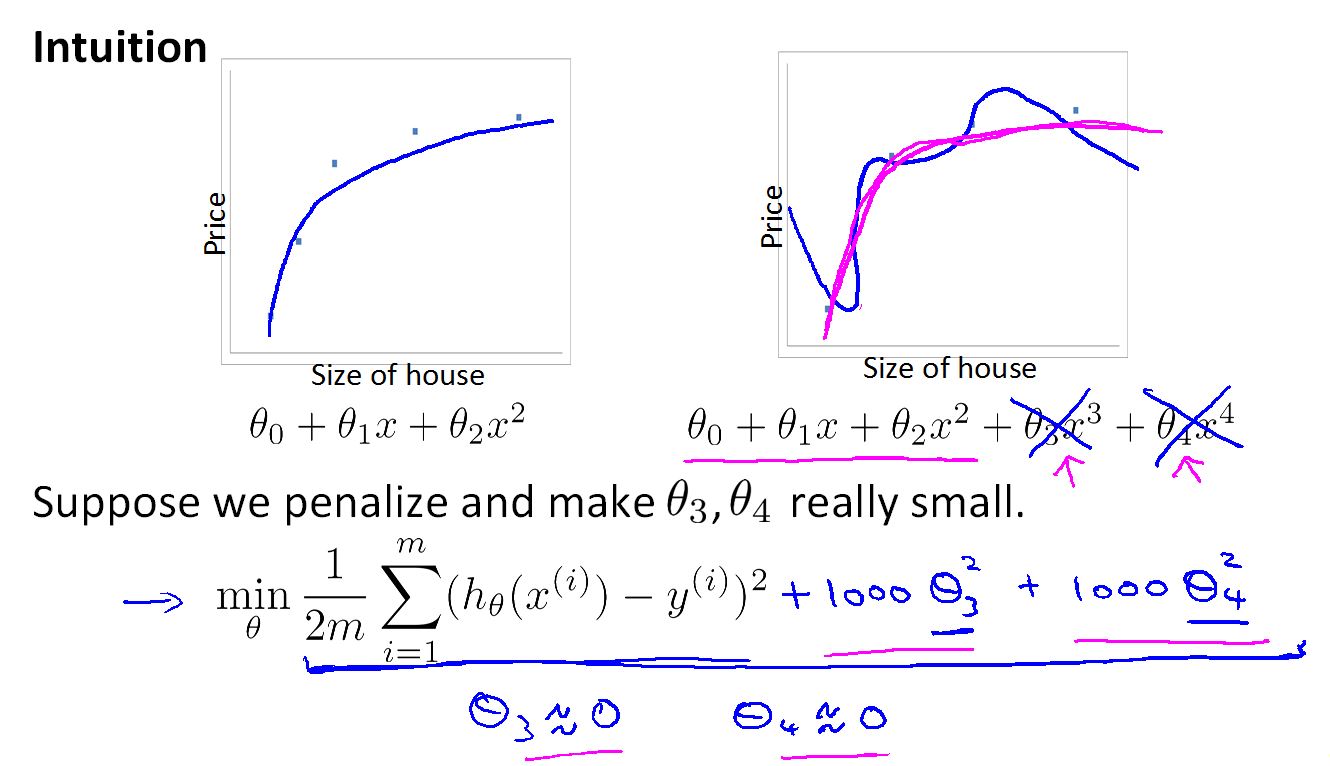
正规化的思想其实就是对参数做惩罚,让拟合曲线变的更圆滑,有更强的泛化能力。
在上图中,加入了对 theta3 和 theta4 的惩罚,拟合曲线由蓝色变成粉红色,而且最后得到的theta3 和 theta4 大概接近于零。
更一般的表示是
这是在Linear regression 和 Logisitic regression 中广泛应用的增加了正规化的代价函数的表现形式。
λ是正规化参数,它在两个目标之间做平衡,一是想让假设更好的拟合训练数据(即代价函数变小) ,二是保持参数值较小,防止其过拟合。
当λ大时,惩罚加重,更好的实现第二个目标,使假设的形式保持简单
当λ小时,更好的实现第一个目标,但过拟合风险加大
当λ很大时,所有被惩罚的项都趋于零,这时假设就会欠拟合
Regularization 在 Linear regression 中的应用
线性回归有两种方法求解拟合曲线的参数:
1.梯度下降法
在加入正规化的思想后优化代价函数:
梯度下降变成:
在这里把theta0单独拿出来,因为在正规化中没有theta0 这一项,在实际操作中也可以加入对 theta0 的惩罚,但对最后的结果不会有太大的影响。
对其做变形:
可以看到加入正规化后梯度函数可以被分成两部分,后一部分是我们已经知道的,而前一部分是说每次更新theta(j)时,我们都对上一轮的theta(j)做了一个处理,具体就是把它和一个小于1大于0的数相乘(相当于对参数进行了压缩,然后在更新)。
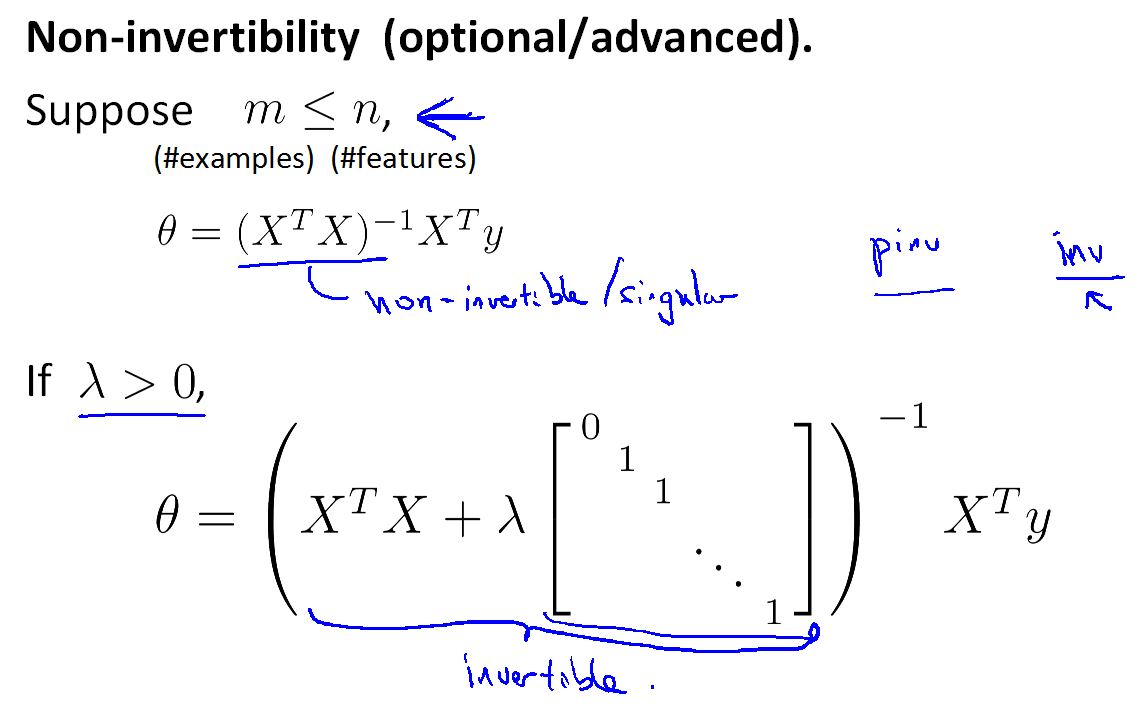
2. 正规方程法
这是求解参数的另一种方法,可以看到,加入正规化方法后,相当于在原来的方程中多加了一项就是,λ乘一个单位矩阵。
加入正规化项还有一个好处,就是以前正规方程法中有一个限制,要处理的数据集矩阵一定要是非奇异的(XTX要可逆),而现在加入正规化项后,没有了这个限制。
Regularization 在 Logistic regression 中的应用
没有加入正规化项的代价函数:
加入正规化项后代价函数变成:
应用梯度下降算法求 theta 的值:










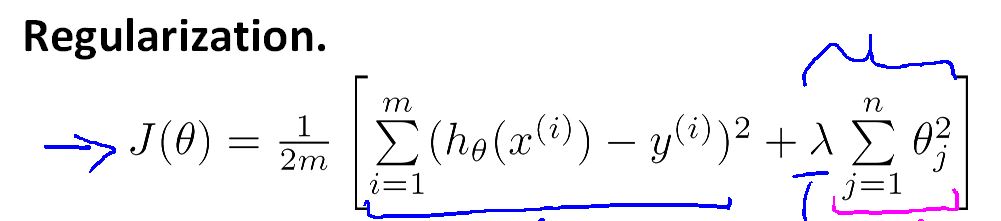
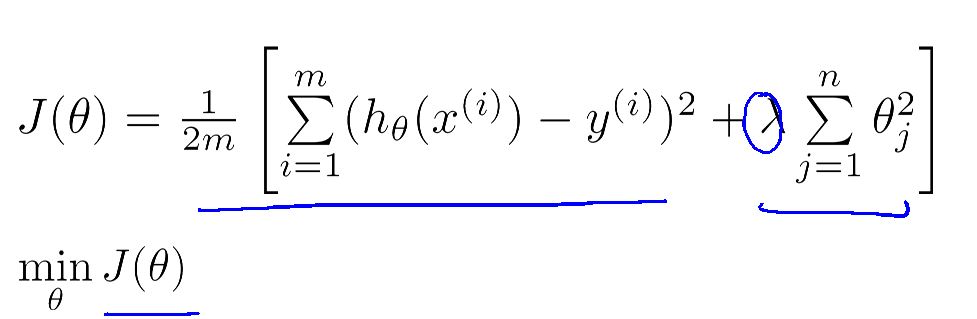
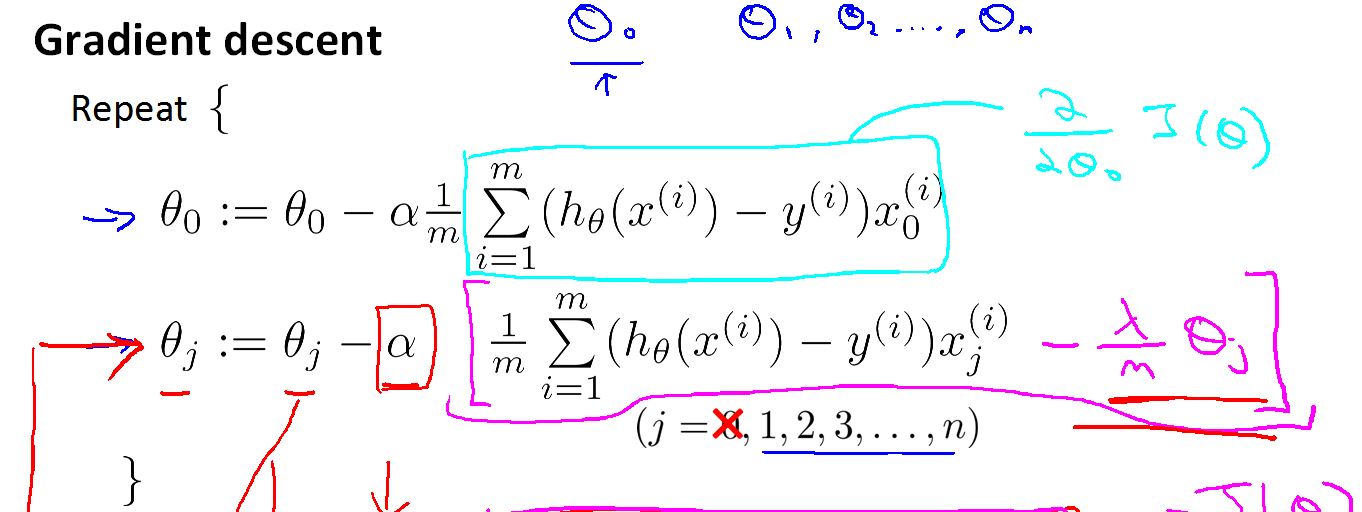
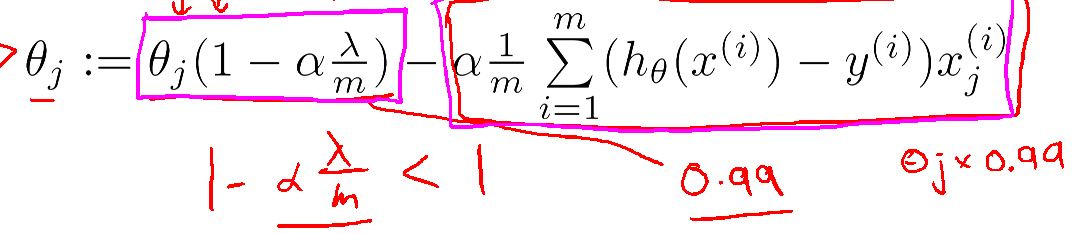

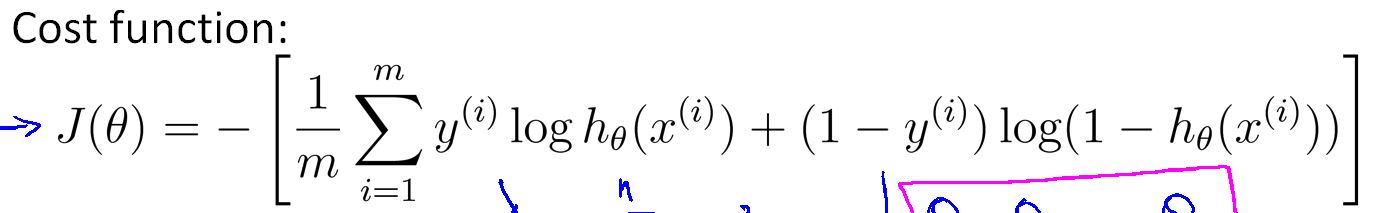
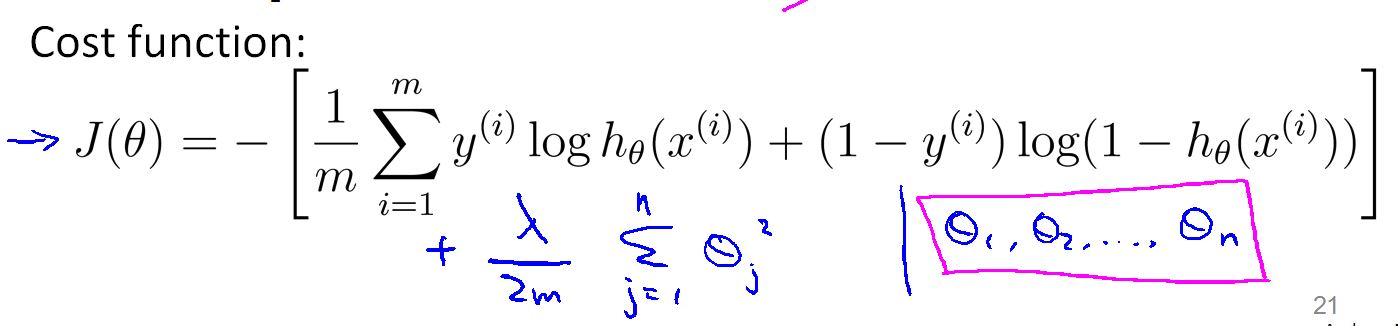















 429
429

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








