有限长序列的频谱分析——DTFT&DFT（答作者问）

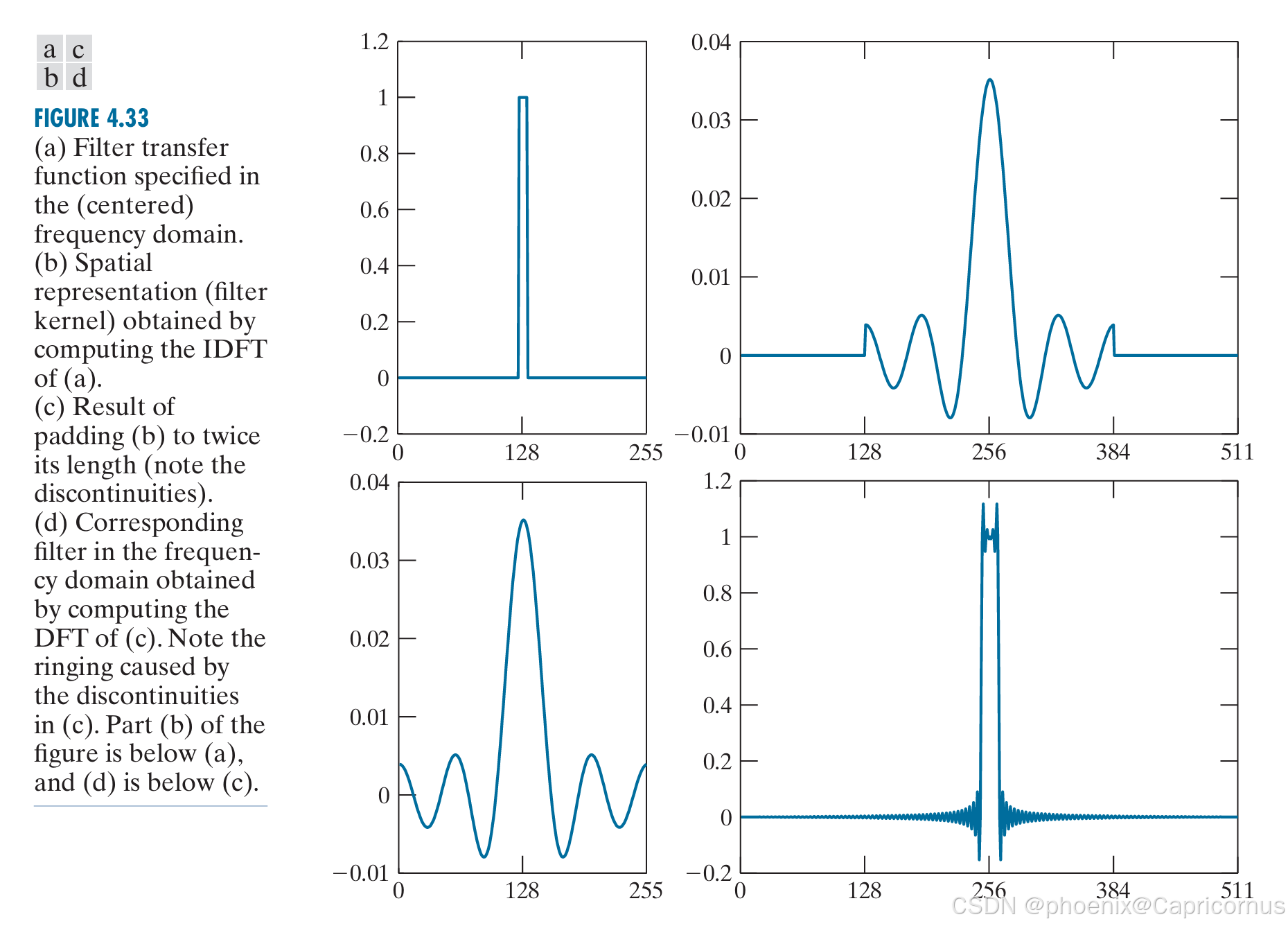
这个问题源自于Rafael Gonzalez的《数字图像处理》中的这幅图，图(c )和图(d)他想干什么？实际上他想说明滤波器零延拓不行（为啥是这样的振荡，频域采样定理会告诉我们，看这里），然后对图像零延拓，真不知道逻辑在哪呢？我在这里仅分析图(c )和图(d)，并上升到理论高度。

Rafael Gonzalez的基础真的是够差的，所以永远都是概念模糊、概念混淆。

在有限长序列的零延拓（补零）——提高频谱的采样频率中讲到有限长序列的零延拓（补零）目的是提高频谱的采样频率。

廖老师的问题是傅里叶变换是一对完全可逆变换，信息没有任何损失，增加频域采样点干嘛？那是和另外一个空域图像对应的傅里叶变换对了。

答：DFT和IDFT当然存在一一对应的时频域映射关系。对有限长序列的频谱分析是看它的DTFT，然而计算机只能计算DFT，时域补零对应频域增加采样点，作用是用DFT近似DTFT。

Get started

这就首先必须理解DTFT和DFT。离散时间傅里叶变换（Discrete-Time Fourier Transform, DTFT）和离散傅里叶变换（Discrete Fourier Transform, DFT）是信号处理中用于分析离散信号的两种数学工具。

离散时间傅里叶变换 (DTFT)

DTFT 是连续傅里叶变换的一种形式，适用于离散时间信号。它将一个离散时间信号转换为一个连续的频域表示。DTFT 的定义如下：

$$X(e^{j\omega })=\sum _{n=-\infty }^{\infty }x[n]e^{-j\omega n}$$

这里$x[n]$是离散时间信号，$X(e^{j\omega })$是该信号的 DTFT，$\omega$是归一化角频率。

DTFT 的一个重要特点是它在频率域上是周期性的，周期为$2\pi$。此外，DTFT 的结果是一个连续函数，这意味着理论上它可以计算任意频率点上的值。

离散傅里叶变换 (DFT)

DFT 是 DTFT 的一种有限样本版本，它只考虑有限长度的序列，并且其输出也是离散的。DFT 通常用于实际应用中，因为计算机只能处理有限数量的数据点。DFT 的定义如下：

$$X[k]=\sum _{n=0}^{N-1}x[n]e^{-j2\pi kn/N}$$

这里$N$是信号的长度，$k$是离散频率索引，$X[k]$是$x[n]$的 DFT。

DFT 与快速傅里叶变换（FFT）密切相关，后者是一种高效的算法，用于计算 DFT。由于 DFT 是离散的，所以它是有限长序列的一个数值计算方法，适合于计算机实现。

DTFT能够更完整的展现信号的频谱。

例子

Let’s look at a simple rectangular pulse,$x[n]=1$ for$0\le n<M$. The DTFT of
$x[n]$ is:

$$X(\omega )=\frac{sin(\omega M/2)}{sin(\omega /2)}{e}^{-j\omega (M-1)/2}$$

Let’s plot$|X(\omega )|$ for$M=8$ over a couple of periods:

Suppose$X_P[k]$ is the P-point DFT of$x[n]$. If$x[n]$ is nonzero only over the finite domain$0\le n<M$, then$X_P[k]$ equals$X(\omega )$ at equally spaced intervals of$\omega$:

$$X_P[k]=X(2\pi k/P),k=0,\dots ,P-1$$

DFT是在DTFT上的等间隔P点采样。

Here’s the 8-point DFT of our 8-point rectangular pulse:

>> x

x =

     1     1     1     1     1     1     1     1

>> X

X =

     8     0     0     0     0     0     0     0

One 8 and a bunch of zeros. That doesn’t seem anything like the DTFT plot above. But when you superimpose the output of |fft| in the right places on the DTFT plot, it all becomes clear.
注释：栅栏效应——当我们将一个连续时间信号采样成离散时间信号，并对其进行 DFT 或 FFT 分析时，实际上是对这个信号的一个有限长度窗口内的样本进行频谱分析。由于 DFT/FFT 的输出是离散的，它只提供了频域内特定频率点上的信息。如果信号包含不在这些离散频率点上的成分，那么这些成分将不能被准确地表示出来，这就好比试图通过栅栏的缝隙观察连续变化的事物一样。

Now you can see that the seven zeros in the output of |fft| correspond to the
seven places (in each period) where the DTFT equals zero.

You can get more samples of the DTFT simply by increasing P. One way to do
that is to zero-pad.

>> x16

x16 =

     1     1     1     1     1     1     1     1     0     0     0     0     0     0     0     0

>> X16 

X16 =

  列 1 至 5

   8.0000 + 0.0000i   1.0000 - 5.0273i   0.0000 + 0.0000i   1.0000 - 1.4966i   0.0000 + 0.0000i

  列 6 至 10

   1.0000 - 0.6682i   0.0000 + 0.0000i   1.0000 - 0.1989i   0.0000 + 0.0000i   1.0000 + 0.1989i

  列 11 至 15

   0.0000 + 0.0000i   1.0000 + 0.6682i   0.0000 + 0.0000i   1.0000 + 1.4966i   0.0000 + 0.0000i

  列 16

   1.0000 + 5.0273i

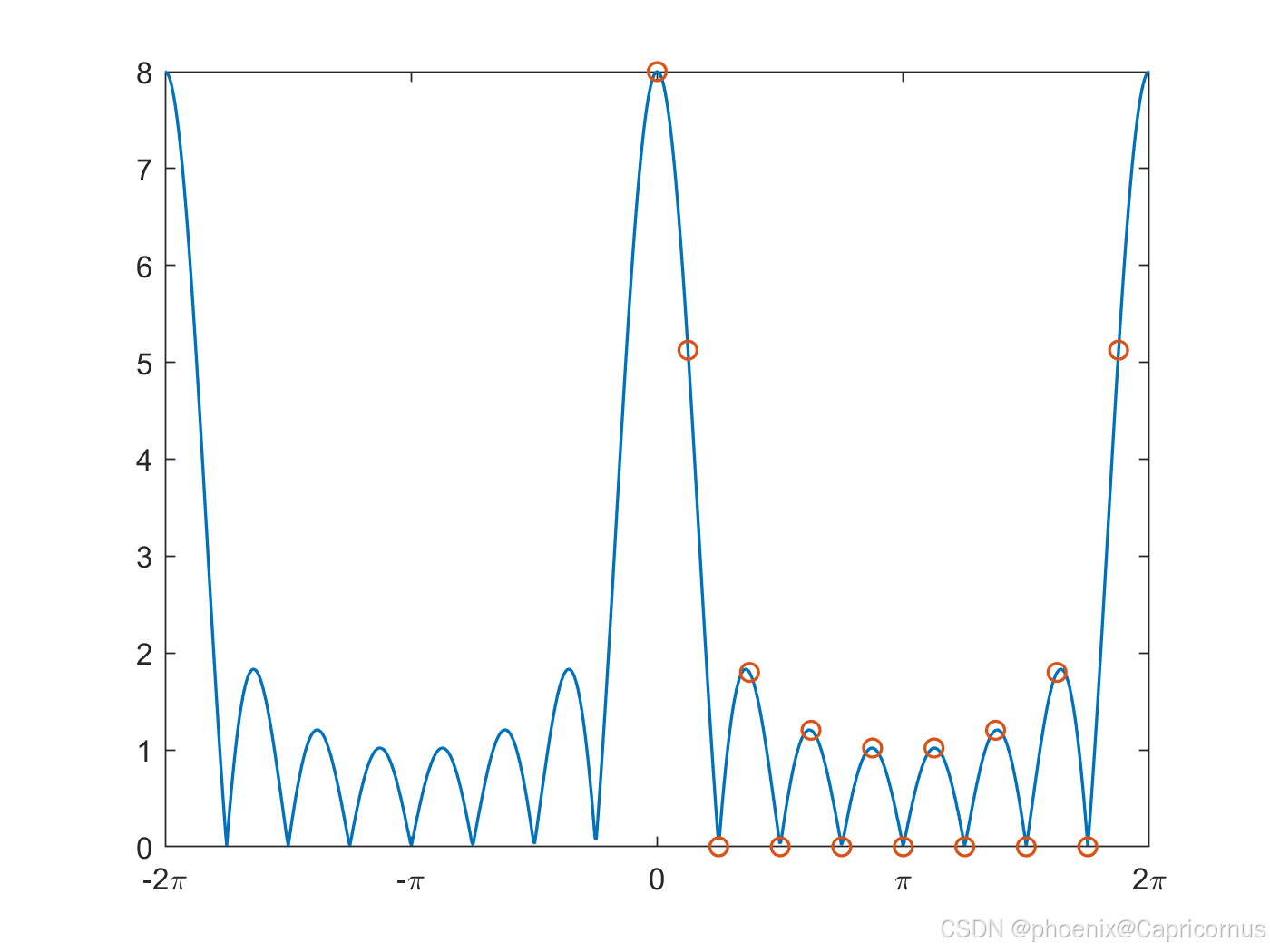
When you tack on a bunch of zeros to a sequence and then compute the DFT, you’re just getting more and more samples of the DTFT of the original sequence.

Another way to increase P is to use the |fft(x,P)| syntax of the |fft| function. This syntax computes the P-point DFT of |x| by using zero-padding.

P = 50;
Xp = fft(x, P)
xp = ifft(Xp)

Xp =

  列 1 至 5

   8.0000 + 0.0000i   6.9422 - 3.2667i   4.2941 - 5.1907i   1.3246 - 5.1588i  -0.6818 - 3.5739i

  列 6 至 10

  -1.1180 - 1.5388i  -0.2984 - 0.1640i   0.8629 + 0.0543i   1.4871 - 0.5888i   1.2549 - 1.3364i

  列 11 至 15

   0.5000 - 1.5388i  -0.1346 - 1.0655i  -0.1947 - 0.3067i   0.2880 + 0.1828i   0.8814 + 0.1113i

  列 16 至 20

   1.1180 - 0.3633i   0.8481 - 0.7964i   0.3237 - 0.8175i  -0.0255 - 0.4060i   0.0649 + 0.1181i

  列 21 至 25

   0.5000 + 0.3633i   0.9176 + 0.1750i   0.9841 - 0.2527i   0.6557 - 0.5425i   0.2055 - 0.4368i

  列 26 至 30

   0.0000 + 0.0000i   0.2055 + 0.4368i   0.6557 + 0.5425i   0.9841 + 0.2527i   0.9176 - 0.1750i

  列 31 至 35

   0.5000 - 0.3633i   0.0649 - 0.1181i  -0.0255 + 0.4060i   0.3237 + 0.8175i   0.8481 + 0.7964i

  列 36 至 40

   1.1180 + 0.3633i   0.8814 - 0.1113i   0.2880 - 0.1828i  -0.1947 + 0.3067i  -0.1346 + 1.0655i

  列 41 至 45

   0.5000 + 1.5388i   1.2549 + 1.3364i   1.4871 + 0.5888i   0.8629 - 0.0543i  -0.2984 + 0.1640i

  列 46 至 50

  -1.1180 + 1.5388i  -0.6818 + 3.5739i   1.3246 + 5.1588i   4.2941 + 5.1907i   6.9422 + 3.2667i


xp =

  列 1 至 10

    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000   -0.0000   -0.0000

  列 11 至 20

    0.0000    0.0000    0.0000    0.0000         0   -0.0000    0.0000   -0.0000    0.0000   -0.0000

  列 21 至 30

    0.0000   -0.0000    0.0000   -0.0000         0   -0.0000    0.0000   -0.0000   -0.0000   -0.0000

  列 31 至 40

   -0.0000   -0.0000   -0.0000    0.0000         0    0.0000   -0.0000    0.0000   -0.0000    0.0000

  列 41 至 50

   -0.0000    0.0000    0.0000   -0.0000         0    0.0000   -0.0000    0.0000    0.0000    0.0000

结论：对8点的rectangular pulse做50点DFT，就是在DTFT上的50点等间隔采样，其IDFT就是8个点为1，其他42个点都为零。有效数据仍然是8位。

总结

对于$N$点长的数据$x(n)$，设$x(n)$的频谱 (DTFT) 为$X(e^{j\omega })$，则

$$X(e^{j\omega })=\text{DTFT}[x(n)]=\sum _{n=0}^{N-1}x(n)e^{-j\omega n}$$

对$x(n)$做$N$点 DFT 运算，由 DFT 与 DTFT 的关系可知，

$$X(k)=X(e^{j\omega }){|}_{\omega =\frac{2\pi }{N}k},k=0,1,\cdots ,N-1$$

如果在数据$x(n)$后面补$M$个零，即 x ′ ( n ) = { x ( n ) , 0 , 0 , ⋯   , 0 } x'(n) = \{x(n), 0, 0, \cdots, 0\} x′(n)={x(n),0,0,⋯,0}，补零序列的频谱为

$$X^{\prime }(e^{j\omega })=\text{DTFT}[x^{\prime }(n)]=\sum _{n=0}^{M+N-1}{x}^{\prime }(n)e^{-j\omega n}$$

$$=\sum _{n=0}^{N-1}x(n)e^{-j\omega n}=X(e^{j\omega })$$

补零前后 DTFT 结果相同，说明 DTFT 结果只取决于有效数据长度，与补零点数无关。

此时对$x^{\prime }(n)$做$N+M$点 DFT 运算，仍然由 DFT 与 DTFT 的关系可知，

$$X^{\prime }(k)=X^{\prime }(e^{j\omega }){|}_{\omega =\frac{2\pi }{N+M}k}=X(e^{j\omega }){|}_{\omega =\frac{2\pi }{N+M}k},k=0,1,\cdots ,N+M-1$$

补零前后 DFT 结果不相同，补零前采样点数为$N$，补零后采样点数增加为$N+M$，采样间隔更密，说明 DFT 结果同数据长度与补零点数都相关。

实际上在计算机中采用的是DFT算法。DFT是对DTFT在频域的均采样，对DTFT的分析相当于是对DFT算法性能在极限情况下的分析，即采样间隔无穷小的极限情况。因此，利用DFT通过补零增加频域采样点，近似DTFT（Plotting the DTFT using the output of fft）。