GATNE：阿里电商场景下的大规模异构网络表示学习 KDD2019

论文链接：https://arxiv.org/pdf/1905.01669.pdf
代码链接：https://github.com/THUDM/GATNE
论文来源：KDD2019

摘要

网络嵌入（图嵌入）在真实世界中已经有了非常大规模的应用，然而现存的一些网络嵌入（图嵌入）相关的方法主要还是集中在同质网络的应用场景下，即节点和边的类型都是单一类型的情况下。但是真实世界网络中每个节点的类型都多种，每条边的类型也有多种，而且每一个节点都具有不同且繁多的属性。所以本论文提出了一种在Attributed Multiplex Heterogeneous Network中进行嵌入学习的统一框架，并提供了充分的数学理论分析，还在数据集Amazon, YouTube, Twitter, and Alibaba上进行了大量的实验。实验结果表明，利用此框架学习到的嵌入有惊人的性能提升，F1 scores可提高5.99-28.23%，而且该框架还成功地部署在全球领先的电子商务公司阿里巴巴集团的推荐系统上。对产品推荐进行离线A/B测试的结果进一步证实了该框架在实践中的有效性和效率。

1、引言

作者根据网络拓扑类型（同构和异构）和属性特征（边、节点）将图分为六类，并总结了当今的发展，如下表所示：

可以看到 AMHEN 的研究是最少的。

本篇论文致力于研究 AMHEN 的表示学习，这种网络的特点在于多种类型的节点可能通过多种类型的边进行关联，并且每个节点都具有不同的属性。

这种结构非常常见，比如作者使用的四种数据集中，超过 15% 的节点对会有超过一种类型的边。举个具体的例子，在电商中，用户可能会对商品具有点击、加购、加收藏等多种交互行为。下图展示了一个真实场景下的异构网络：

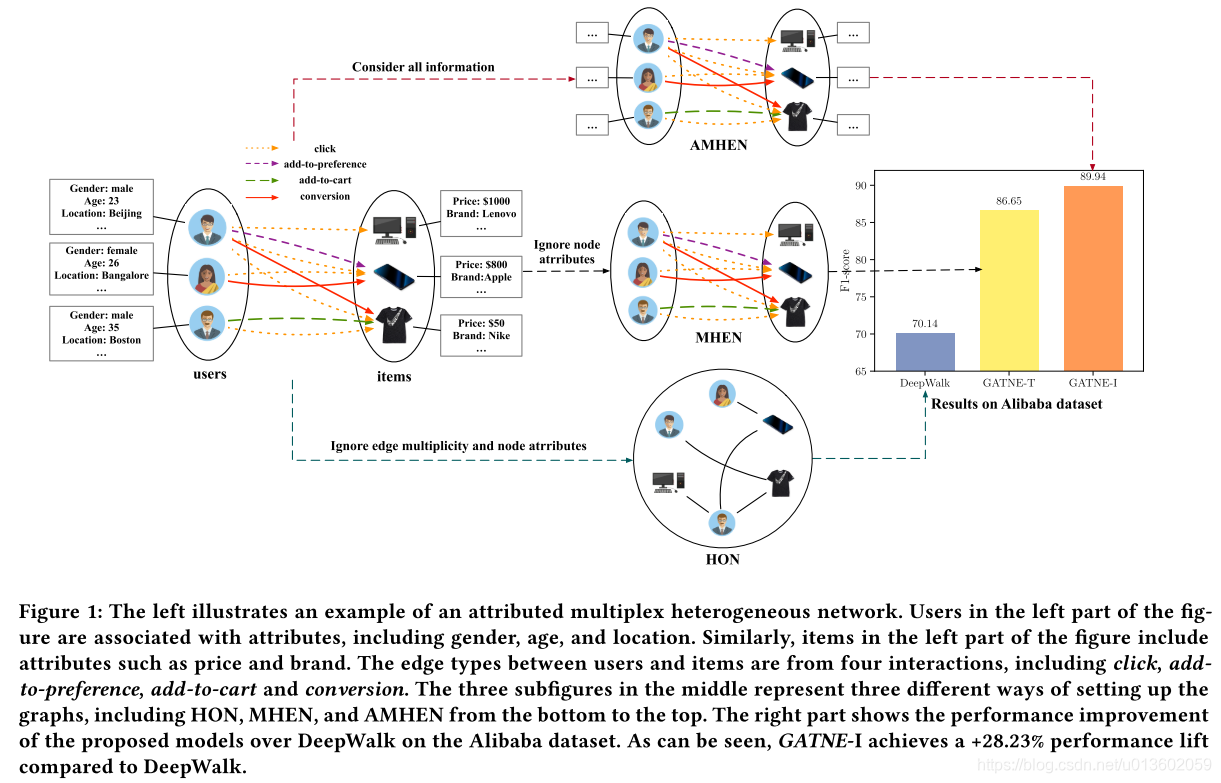
图的左边用户和商品都分别有多个属性，而且用户和商品之间的连边类型也是多样的，一个用户和一个商品可能有多个类型不同的连边。图的中间部分是将左边的图分别形式化为了：AMHEN(属性多重异质网)、MHEN(多重异质网)和HON(同质网)。右边是，三种方法的实验效果对比。

传统的 Graph Embedding 方法比如 DeepWalk 的做法都是直接忽略图中边的类型以及节点的特征，将真实网络建模为 HON。而如果将边类型考虑进去建模为 MHEN，则会取得非常明显的效果。最后，如果还能够将节点的属性也考虑进去建模为 AMHEN，那么就充分利用到了原图的所有信息，这样便可以得到最好的效果。

除了异构性和多样性外，处理 AMHEN 也面临着多重挑战：

• 多路复用的边（Multiplex Edges）：每个节点对可能含有多种不同的类型边；
• 归纳学习（Inductive）：如何解决冷启动问题；
• 可扩展性（Scalability），如何拓展到大规模网络中。

为了解决这些问题，作者提出了一种通用的多路复用异构网络嵌入学习框架（General Attributed Multiplex HeTerogeneous Network Embedding，GATNE）， 并用于捕获节点丰富的属性信息和来自不同节点类型的多路复用拓扑结构。

2、GATNE模型

本节介绍两种类型的 GATNE 框架，包括直推式学习范式的 GATNE-T 和归纳式学习范式的 GATNE-I。

2.1、GATNE-T模型

我们先从多路复用的异构网络图开始，并介绍 GATNE-T 模型。

GATNE-T 考虑 Base Embedding 和 Edge Embedding（这里的 Edge Embedding 并不是对边进行 Embedding，而是基于 edge type 进行聚合得到 Embedding），如下图紫色边所示。

节点的 Base Embedding 对所有类型的边共享。

第 $k$ 层 $v_i$ 节点的 edge type $r$ 类型的 Edge Embedding 如下所示：$$u_{i,r}^{(k)}=aggregator\left(\left\{u_{j,r}^{(k-1)},\forall v_j\in {\mathcal{N}}_{i,r}\right\}\right)$$其中， ${\mathcal{N}}_{i,r}$为节点 $v_i$基于 edge type $r$ 的邻居； $u_{i,r}^{(0)}$是随机初始化的。

聚合函数可以为均值聚合、最大池化聚合等：$$u_{i,r}^{(k)}=\sigma \left({\hat{W}}^{(k)}\cdot mean\left(\left\{u_{j,r}^{(k-1)},\forall v_j\in {\mathcal{N}}_{i,r}\right\}\right)\right)$$$$u_{i,r}^{(k)}=max(\{\sigma ({\hat{W}}_{pool}^{(k)}{u}_{j,r}^{(k-1)}+{\hat{b}}_{}$$