说明:以下涉及到的一些公式以及图片来自于Learning OpenCV。
做了快2个月的立体相机标定,遇到了一些问题,也有了一些体会,在这里记下来。
1.在做立体相机标定的时候,标定板的规范与否直接影响到最后标定的结果,进而会影响目标3D坐标重建。
这里说的规范指的是,打印的棋盘格(或者圆点)需要保证每个square都是严格大小一致的,即打印出来后每个棋盘格大小应一样;打印出来的棋盘格要尽量平整的附在某一平面或者玻璃板上,然后才能用来拍摄标定图像;测量squareSize的时候,要尽可能的精确,也就是说,棋盘格的实际物理尺寸对标定结果影响很大。
对左右相机出来图像要有深刻的理解,左图的目标处于相对偏右的位置,左右相机出来的图像千万不要弄反了,建议选取10对以上的图像对做标定。
2.立体相机标定的一些概念
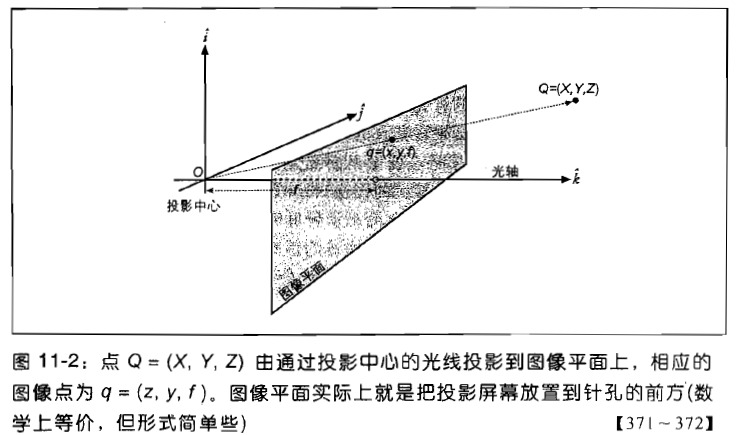
2.1.相机投影
像素平面上的点q(x,y)与世界中的点Q(X,Y,Z)的变换对应关系为:
x = fx(X/Z)+cx,y = fy(Y/Z) + cy;
写成矩阵的形式:
2.2.透镜畸变
理论上面可能定义一种透镜而不引入任何畸变&#








 本文详细介绍了基于OpenCV的立体相机标定过程,强调了标定板规范、图像理解的重要性,并解析了相机投影、透镜畸变、立体成像、对极几何等概念。通过标定获取相机内外参数,用于目标三维坐标计算,最后提供了标定步骤和参数解释。
本文详细介绍了基于OpenCV的立体相机标定过程,强调了标定板规范、图像理解的重要性,并解析了相机投影、透镜畸变、立体成像、对极几何等概念。通过标定获取相机内外参数,用于目标三维坐标计算,最后提供了标定步骤和参数解释。
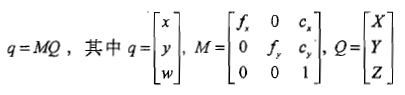
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1212
1212

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








