SPSS统计学：成对样本t检验/配对样本t检验/重复测量t检验

概念

成对样本t检验（Paired Sample t-Test），也称为配对样本t检验或重复测量t检验，是一种统计方法，用于比较两个相关或配对的样本均值之间的差异是否显著。

用途

这种检验通常用于以下情况：

1. 同一样本的两次测量：例如，同一组受试者在不同时间点的测量结果。
2. 两个相关的样本：例如，同一组受试者在实验前后的测量结果，或者两个相关群体（如双胞胎）的比较。

成对样本t检验的基本假设是两个样本来自同一总体，或者它们是配对的，这意味着每个样本中的一个观测值可以与另一个样本中的一个观测值相匹配。

检验步骤

1. 计算差值：对于每一对样本，计算它们之间的差值。

2. 计算差值的平均值和标准差：计算所有差值的平均值（差值的均值）和标准差。

3. 计算t统计量：使用以下公式计算t统计量：
   
   

4. 确定自由度：自由度（df）通常是 n - 1。

5. 查找临界t值或计算p值：根据自由度和显著性水平（如0.05），查找临界t值或计算p值。

6. 做出决策：如果计算出的t统计量大于临界t值，或者p值小于显著性水平，则拒绝原假设，认为两个样本之间存在显著差异。

成对样本t检验是分析配对数据的有力工具，它考虑了样本之间的相关性，从而提高了检验的精确度。

举例

我们通过一个具体的例子来详细说明成对样本t检验的计算步骤。假设我们有一组数据，记录了10名学生在数学测试中使用两种不同教学方法前后的得分。

SPSS计算

手动计算

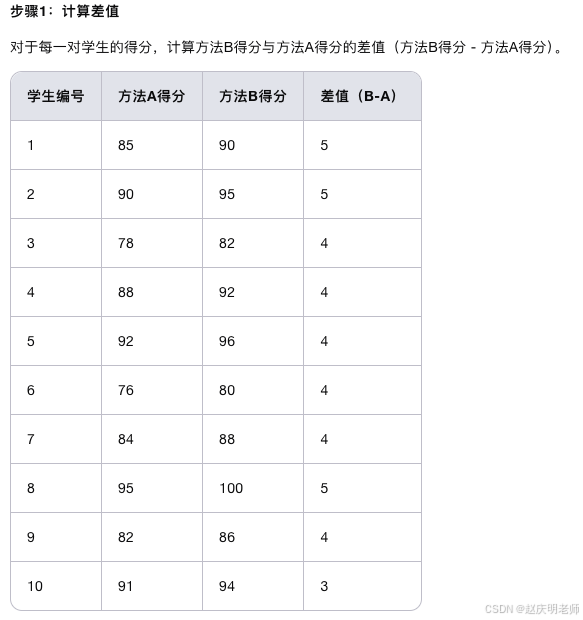
计算结果与SPSS一致

步骤5：查找临界t值或计算p值
对于自由度为9，显著性水平为0.05的双尾检验，临界t值约为2.262（通过查表获得）。由于计算出的t统计量（21）远大于临界t值，我们可以拒绝原假设。
也可以根据显著性0.000小于0.05，从而判断可以拒绝零假设。

步骤6：做出决策
由于t统计量远大于临界t值，我们得出结论：两种教学方法的得分存在显著差异。