python 实现一个简单的动态目标自动实时追踪

斐夷所非

已于 2024-12-18 17:15:18 修改

阅读量1k

点赞数 27

分类专栏： clean code 文章标签：动态目标实时追踪

于 2024-09-22 00:38:53 首次发布

本文链接：https://blog.csdn.net/u013669912/article/details/142422583

版权

clean code 专栏收录该内容

49 篇文章

订阅专栏

注：本文为 “动态目标实时追踪” 相关文章合辑。

一个简单的导弹自动追踪以及实时图片旋转算法，Python-pygame 代码实现

半壶砂博客园 posted @ 2017-12-07 11:43

自动追踪算法，在设计 2D 射击类游戏时经常会用到，这个听起来很高大上的东西，其实也并不是军事学的专利，在数学上解决的话需要去解微分方程，

这个没有点数学基础是很难算出来的。但是有了计算机就不一样了，依靠计算机极快速的运算速度，利用微分的思想，加上一点简单的三角学知识，就可以实现它。

话不多说，来看看它的算法原理，看图：

初始状态

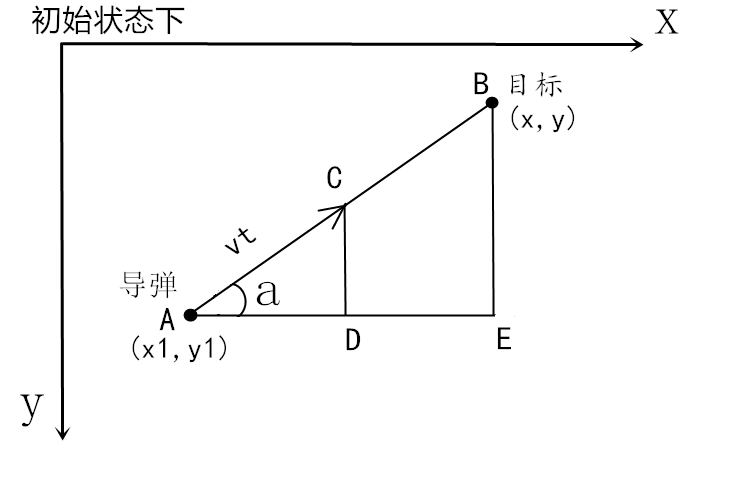
由于待会要用 pygame 演示，他的坐标系是 y 轴向下，所以这里也用 y 向下的坐标系。

算法总的思想就是根据上图，把时间 t 分割成足够小的片段（比如 1/1000，这个时间片越小越精确），每一个片段分别构造如上三角形，计算出导弹下一个时间片走的方向（即∠a）和走的路程（即 vt=|AC|），这时候目标再在第二个时间片移动了位置，这时刚才计算的 C 点又变成了第二个时间片的初始点，这时再在第二个时间片上在 C 点和新的目标点构造三角形计算新的 vt，然后进入第三个时间片，如此反复即可。

假定导弹和目标的初始状态下坐标分别是 (x1,y1),(x,y)，构造出直角三角形 ABE，这个三角形用来求∠a 的正弦和余弦值，因为 vt 是自己设置的，需要计算 A 到 C 点 x 和 y 坐标分别移动了多少，移动的值就是 AD 和 CD 的长度，这两个分别用 vt 乘 cosa 和 sina 即可。

计算 sina 和 cosa，正弦对比斜，余弦邻比斜，斜边可以利用两点距离公式计算出，即：

$\left| \text{A}\left. \text{B} \right| \right.=\sqrt{{{(x-{{x}_{1}})}^{2}}+{{({{y}_{1}}-y)}^{2}}}$

于是

$\displaystyle\sin a=\frac{{{y}_{^{1}}}-y}{|AB|}$

$\displaystyle\cos a=\frac{x-{{x}_{1}}}{|AB|}$

AC 的长度就是导弹的速度乘以时间即 |AC|=vt，然后即可计算出 AD 和 CD 的长度，于是这一个时间片过去后，导弹应该出现在新的位置 C 点，他的坐标就是老的点 A 的 x 增加 AD 和 y 减去 CD。

于是，新的 C 点坐标就是：

$C({{x}_{2}},{{y}_{2}})=({{x}_{1}}=AC*\cos a,{{y}_{1}}-AC*\sin a)$

只要一直反复循环执行这个操作即可，好吧，为了更形象，把第一个时间片和第二个时间片放在一起看看：

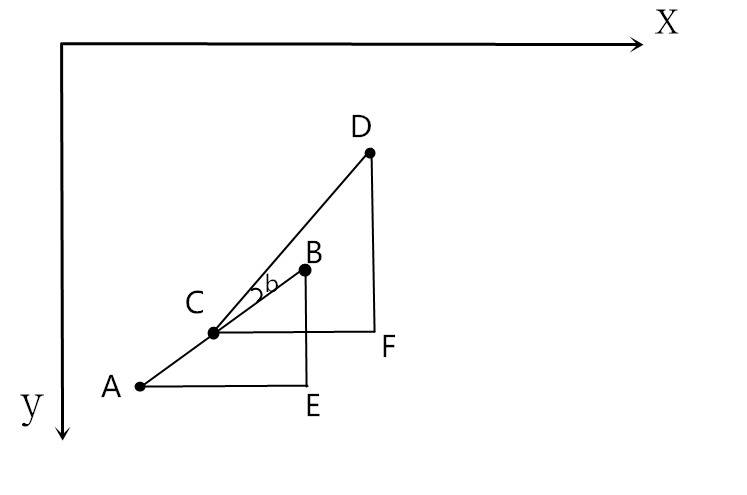
第一个是时间片构造出的三角形是 ABE，经过一个时间片后，目标从 B 点走到了 D 点，导弹此时在 C 点，于是构造新的三角形 CDF，重复刚才的计算过程即可，图中的角∠b 就是导弹需要旋转的角度，现实中只需要每个时间片修正导弹的方向就可以了，具体怎么让导弹改变方向，这就不是需要研究的问题了

接下来就用 pygame 来演示一下这个效果，效果如下图：

很简单的代码如下：

 1 import pygame,sys
 2 from math import *
 3 pygame.init()
 4 screen=pygame.display.set_mode((800,700),0,32)
 5 missile=pygame.image.load('element/red_pointer.png').convert_alpha()
 6 x1,y1=100,600           #导弹的初始发射位置
 7 velocity=800            #导弹速度
 8 time=1/1000             #每个时间片的长度
 9 clock=pygame.time.Clock()
10 old_angle=0
11 while True:
12     for event in pygame.event.get():
13         if event.type==pygame.QUIT:
14             sys.exit()
15     clock.tick(300)
16     x,y=pygame.mouse.get_pos()          #获取鼠标位置，鼠标就是需要打击的目标
17     distance=sqrt(pow(x1-x,2)+pow(y1-y,2))      #两点距离公式
18     section=velocity*time               #每个时间片需要移动的距离
19     sina=(y1-y)/distance
20     cosa=(x-x1)/distance
21     angle=atan2(y-y1,x-x1)              #两点线段的弧度值
22     x1,y1=(x1+section*cosa,y1-section*sina)
23     d_angle = degrees(angle)        #弧度转角度
24     screen.blit(missile, (x1-missile.get_width(), y1-missile.get_height()/2))
25     dis_angle=d_angle-old_angle          #dis_angle就是到下一个位置需要改变的角度
26     old_angle=d_angle                    #更新初始角度
27     pygame.display.update()

如果仅把导弹考虑为一个质点，那么以上算法就已经足矣，没有做导弹的旋转，因为一个质点也不分头尾不需要旋转，当然这前提得是加载的导弹图片很小的时候不旋转看起来也没什么问题。

但是在 pygame 里面做旋转并不是一件容易的事情(也可能是无知)，先把图片替换成一张矩形的，再加入旋转函数看看效果如何

missiled = pygame.transform.rotate(missile, -(d_angle))
screen.blit(missiled, (x1-missile.get_width(), y1-missile.get_height()/2))

因为图片的坐标点是它的左上角的点，所以如果想让图片的坐标固定在箭头尖点，那么把图片实际打印位置 x 减少图片长度，y 减少一半宽度就行。

但是实际运行效果并不好：

大致方向相同，但是图片箭头的尖点并没有一直跟随鼠标，这是为什么呢？

经过研究（就因为这个问题没解决一直没发布），发现原来是这个图旋转的机制问题，看看旋转后的图片变成什么样了：

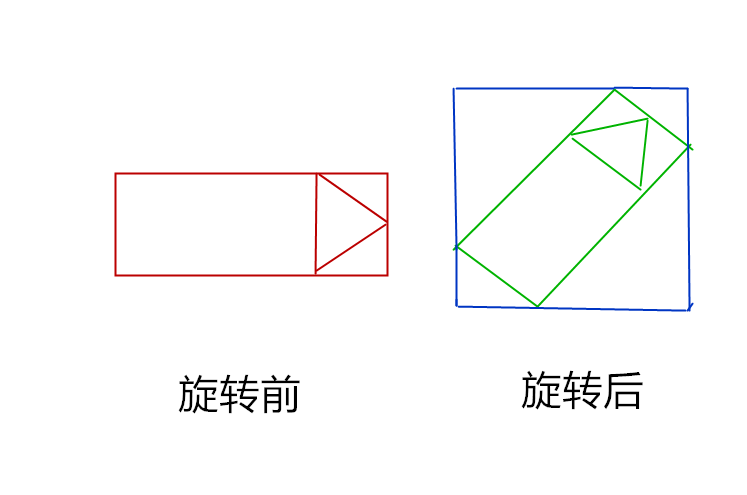
旋转后的图片变成了蓝色的那个范围，根据旋转角度的不同，所变成的图片大小也不一样，看旋转 90 的情况

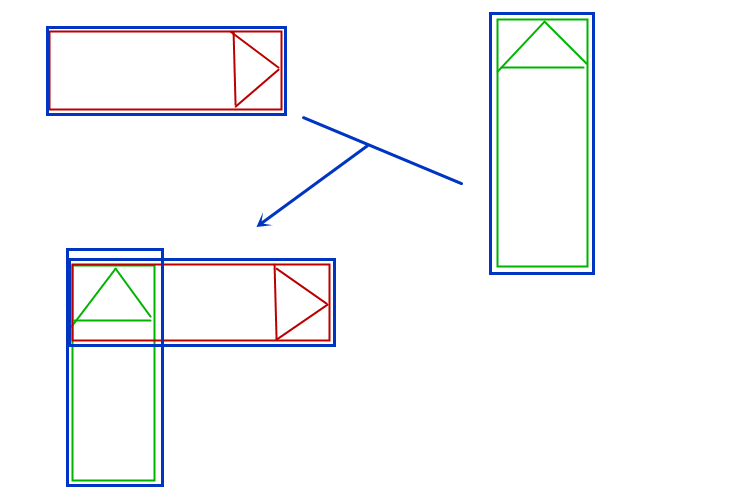
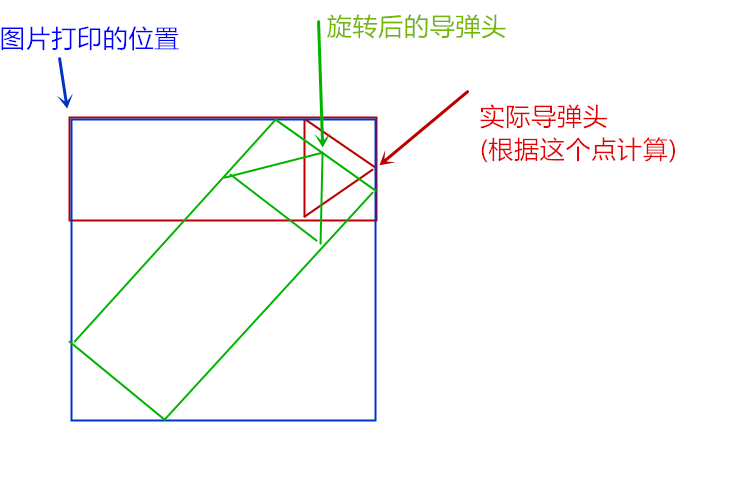
发现，旋转后的图片不仅面积变大了，导弹头的位置也变了。那应该怎么解决这个问题呢？

思路是，每一次旋转图片以后，求出旋转图的头位置（图中的绿色箭头点），然后把绿图的打印位置移动一下下， $x ， y$ 分别移动两个头的距离，就可以让旋转后的导弹头对准实际参与运算的那个导弹头的位置，移动后应该是这样的：

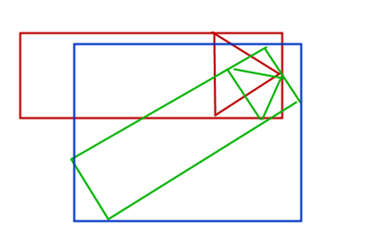
这样，两个导弹头的点就一致了。接下来分析求旋转后的导弹头的算法。根据旋转角度的不同，旋转角在不同象限参数不一样，所以分为这四种情况

1，2 象限

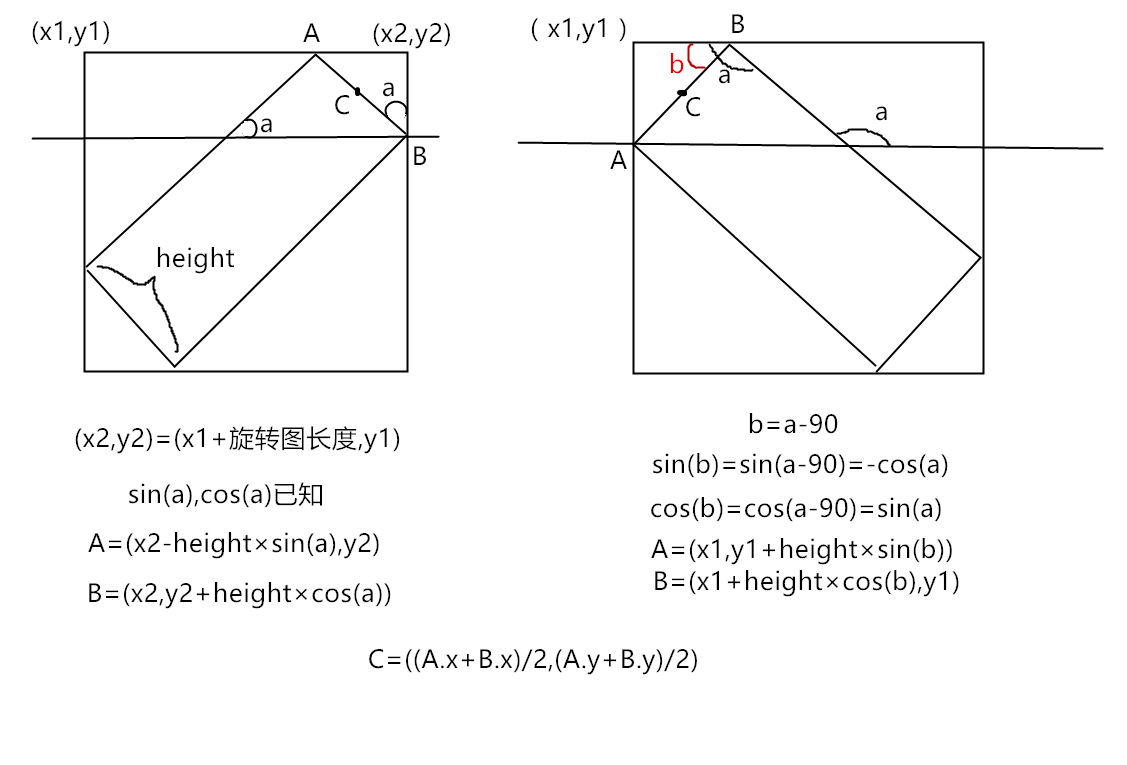
3，4 象限，它的旋转只有正负 0—180，所以 3，4 象限就是负角

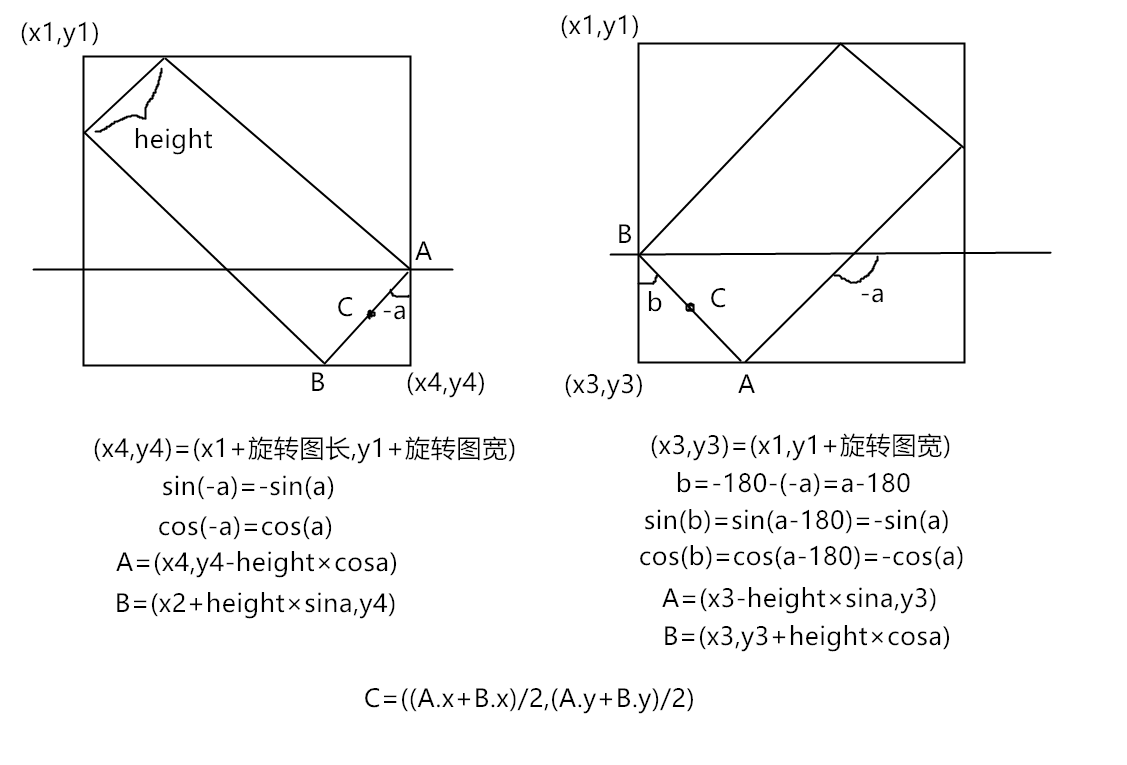
显示图片的时候将它移动

screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))

这里的 $x_1-width, y_1-height/2)$ 其实才是上图中的 $x_1,y_1)$

所以最后加入相关算法代码，效果就比较完美了

大功告成，最后附上全部的算法代码

 1 import pygame,sys
 2 from math import *
 3 pygame.init()
 4 font1=pygame.font.SysFont('microsoftyaheimicrosoftyaheiui',23)
 5 textc=font1.render('*',True,(250,0,0))
 6 screen=pygame.display.set_mode((800,700),0,32)
 7 missile=pygame.image.load('element/rect1.png').convert_alpha()
 8 height=missile.get_height()
 9 width=missile.get_width()
10 pygame.mouse.set_visible(0)
11 x1,y1=100,600           #导弹的初始发射位置
12 velocity=800            #导弹速度
13 time=1/1000             #每个时间片的长度
14 clock=pygame.time.Clock()
15 A=()
16 B=()
17 C=()
18 while True:
19     for event in pygame.event.get():
20         if event.type==pygame.QUIT:
21             sys.exit()
22     clock.tick(300)
23     x,y=pygame.mouse.get_pos()          #获取鼠标位置，鼠标就是需要打击的目标
24     distance=sqrt(pow(x1-x,2)+pow(y1-y,2))      #两点距离公式
25     section=velocity*time               #每个时间片需要移动的距离
26     sina=(y1-y)/distance
27     cosa=(x-x1)/distance
28     angle=atan2(y-y1,x-x1)              #两点间线段的弧度值
29     fangle=degrees(angle)               #弧度转角度
30     x1,y1=(x1+section*cosa,y1-section*sina)
31     missiled=pygame.transform.rotate(missile,-(fangle))
32     if 0<=-fangle<=90:
33         A=(width*cosa+x1-width,y1-height/2)
34         B=(A[0]+height*sina,A[1]+height*cosa)
35 
36     if 90<-fangle<=180:
37         A = (x1 - width, y1 - height/2+height*(-cosa))
38         B = (x1 - width+height*sina, y1 - height/2)
39 
40     if -90<=-fangle<0:
41         A = (x1 - width+missiled.get_width(), y1 - height/2+missiled.get_height()-height*cosa)
42         B = (A[0]+height*sina, y1 - height/2+missiled.get_height())
43 
44     if -180<-fangle<-90:
45         A = (x1-width-height*sina, y1 - height/2+missiled.get_height())
46         B = (x1 - width,A[1]+height*cosa )
47         
48     C = ((A[0] + B[0]) / 2, (A[1] + B[1]) / 2)
49 
50     screen.fill((0,0,0))
51     screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))
52     screen.blit(textc, (x,y)) #鼠标用一个红色*代替
53     pygame.display.update()

Unity 导弹自动追踪算法

示申○言舌已于 2022-03-29 21:46:22 修改

网上找了很久，没有找到满意的追踪算法，要么是 2D 的，要么就不逼真，只好自己硬憋了1天，终于硬憋出来了，效果图：

（这个图是最初版本的效果，完善后的项目请见下方链接）

视频演示

导弹追踪算法演示

核心代码：

using UnityEngine;
 
[RequireComponent(typeof(Collider),typeof(AudioSource))]
public class Missile : MonoBehaviour
{
    [SerializeField, Tooltip("最大转弯速度")]
    private float MaximumRotationSpeed = 120.0f;
 
    [SerializeField, Tooltip("加速度")]
    private float AcceleratedVeocity = 12.8f;
 
    [SerializeField, Tooltip("最高速度")]
    private float MaximumVelocity = 30.0f;
 
    [SerializeField, Tooltip("生命周期")]
    private float MaximumLifeTime = 8.0f;
 
    [SerializeField, Tooltip("上升期时间")]
    private float AccelerationPeriod = 0.5f;
 
    [SerializeField, Tooltip("爆炸特效预制体")]
    private Explosion[] ExplosionPrefabs = null;
 
    [SerializeField, Tooltip("导弹渲染体组件")]
    private Renderer MissileRenderer = null;
 
    [SerializeField, Tooltip("尾焰及烟雾粒子特效")]
    private ParticleSystem[] MissileEffects = null;
 
    [HideInInspector]
    public Transform Target = null;        // 目标
    [HideInInspector]
    public float CurrentVelocity = 0.0f;   // 当前速度
 
    private AudioSource audioSource = null;   // 音效组件
    private float lifeTime = 0.0f;            // 生命期
 
    private void Start()
    {
        audioSource = GetComponent<AudioSource>();
        audioSource.loop = true;
        if (!audioSource.isPlaying)
            audioSource.Play();
    }
    
    // 爆炸
    private void Explode()
    {
        // 之所以爆炸时不直接删除物体，而是先禁用一系列组件，
        // 是因为导弹产生的烟雾等效果不应该立即消失
 
        // 禁止所有碰撞器
        foreach( Collider col in GetComponents<Collider>())
        {
            col.enabled = false;
        }
        // 禁止所有粒子系统
        foreach( ParticleSystem ps in MissileEffects)
        {
            ps.Stop();
        }
        // 停止播放音效
        if (audioSource.isPlaying)
            audioSource.Stop();
 
        // 停止渲染，停止本脚本，随机实例化爆炸特效，删除本物体
        MissileRenderer.enabled = false;
        enabled = false;
        Instantiate(ExplosionPrefabs[Random.Range(0, ExplosionPrefabs.Length)], transform.position, Random.rotation);
 
        // 三秒后删除导弹物体，这时候烟雾已经散去，可以删掉物体了
        Destroy(gameObject, 3.0f);
    }
 
    private void Update()
    {
        float deltaTime = Time.deltaTime;
        lifeTime += deltaTime;
 
        // 如果超出生命周期，则直接爆炸。
        if( lifeTime > MaximumLifeTime )
        {
            Explode();
            return;
        }
 
        // 计算朝向目标的方向偏移量，如果处于上升期，则忽略目标
        Vector3 offset =
            ((lifeTime < AccelerationPeriod) && (Target != null))
            ? Vector3.up
            : (Target.position - transform.position).normalized;
 
        // 计算当前方向与目标方向的角度差
        float angle = Vector3.Angle(transform.forward, offset);
        
        // 根据最大旋转速度，计算转向目标共计需要的时间
        float needTime = angle / ( MaximumRotationSpeed * ( CurrentVelocity / MaximumVelocity ));
 
        // 如果角度很小，就直接对准目标
        if (needTime < 0.001f)
        {
            transform.forward = offset;
        }
        else
        {
            // 当前帧间隔时间除以需要的时间，获取本次应该旋转的比例。
            transform.forward = Vector3.Slerp(transform.forward, offset, deltaTime / needTime).normalized;
        }
 
        // 如果当前速度小于最高速度，则进行加速
        if (CurrentVelocity < MaximumVelocity )
            CurrentVelocity += deltaTime * AcceleratedVeocity;
        
        // 朝自己的前方位移
        transform.position += transform.forward * CurrentVelocity * deltaTime;
    }
 
    private void OnTriggerEnter(Collider other)
    {
        // 当发生碰撞，爆炸
        Explode();
    }
}

最新版本

猛击此处，点击查看视频演示

猛击此处，下载演示升级版（带导弹各种参数调整UI）

猛击此处下载工程源代码

via:

一个简单的导弹自动追踪以及实时图片旋转算法，Python-pygame代码实现 - 半壶砂 - 博客园 posted @ 2017-12-07 11:43

https://www.cnblogs.com/halfsand/p/7976636.html
Unity导弹自动追踪算法_unity 雷达跟踪计算-CSDN博客 示申○言舌已于 2022-03-29 21:46:22 修改

https://blog.csdn.net/sdhexu/article/details/77962134