Binary Number | 1’s and 2’s complement / one’s and two’s

注：本文为 “1’s and 2’s complement” 相关文章合辑。

机翻，未校。

如有内容异常，请看原文。

---

1’s and 2’s complement of a Binary Number

二进制数的 1 和 2 的补码

Last Updated : 15 Dec, 2022

Given a Binary Number as a string, print its 1’s and 2’s complements.

给定一个二进制数作为字符串，打印它的 1 和 2 的补码。

1’s complement of a binary number is another binary number obtained by toggling all bits in it, i.e., transforming the 0 bit to 1 and the 1 bit to 0.In the 1’s complement format , the positive numbers remain unchanged . The negative numbers are obtained by taking the 1’s complement of positive counterparts.
一个二进制数的 1 的补码是另一个二进制数，通过翻转其中所有的位得到，即将 0 位转换为 1，将 1 位转换为 0。 在 1 的补码格式中，正数保持不变。 负数是通过对相应的正数取 1 的补码来获得的。

for example +9 will be represented as 00001001 in eight-bit notation and -9 will be represented as 11110110, which is the 1’s complement of 00001001.
例如，+9 将表示为 00001001 以 8 位表示法，-9 将表示为 11110110，这是 1 的 00001001 的补码。

Examples: 例子：

1's complement of "0111" is "1000"
1's complement of "1100" is "0011"

2’s complement of a binary number is 1, added to the 1’s complement of the binary number. In the 2’s complement representation of binary numbers, the MSB represents the sign with a ‘0’ used for plus sign and a ‘1’ used for a minus sign. the remaining bits are used for representing magnitude. positive magnitudes are represented in the same way as in the case of sign-bit or 1’s complement representation. Negative magnitudes are represented by the 2’s complement of their positive counterparts.
二进制数的 2 的补数是 1，加上二进制数的 1 补码。在二进制数的 2 补码表示中，MSB 表示符号，“0”用于加号，“1”用于减号。其余位用于表示幅度。正幅度的表示方式与 sign-bit 或 1 的补码表示方式相同。 负星等由其正对应物的 2 的补数表示。

Examples: 例子：

2's complement of "0111" is "1001"
2's complement of "1100" is "0100"

Another trick to finding two’s complement:

求 2 补码的另一个技巧：

Step 1: Start from the Least Significant Bit and traverse left until you find a 1. Until you find 1, the bits stay the same
第 1 步： 从最低有效位开始，向左遍历，直到找到 1。 在找到 1 之前，位保持不变

Step 2: Once you have found 1, let the 1 as it is, and now
第 2 步：找到 1 后，让 1 保持原样，现在

Step 3: Flip all the bits left into the 1.
第 3 步：将剩余的所有位翻转到 1 中。

Illustration

示例

Suppose we need to find 2s Complement of 100100
假设我们需要找到 100100 的 2 个补码

Step 1: Traverse and let the bit stay the same until you find 1. Here x is not known yet. Answer = xxxx00 –
第 1 步： 遍历并让位保持不变，直到找到 1。这里 x 尚未知。答案 = xxxx00 –

Step 2: You found 1. Let it stay the same. Answer = xxx100
第 2 步：您找到了 1.让它保持不变。答案 = xxx100

Step 3: Flip all the bits left into the 1. Answer = 011100.
第 3 步：将剩余的所有位翻转到 1 中。答案 = 011100。

Hence, the 2s complement of 100100 is 011100.
因此，100100 的 2s 补码是 011100。

For one’s complement, we simply need to flip all bits.For 2’s complement, we first find one’s complement. We traverse the one’s complement starting from LSB (least significant bit), and look for 0. We flip all 1’s (change to 0) until we find a 0. Finally, we flip the found 0. For example, 2’s complement of “01000” is “11000” (Note that we first find one’s complement of 01000 as 10111). If there are all 1’s (in one’s complement), we add an extra 1 in the string. For example, 2’s complement of “000” is “1000” (1’s complement of “000” is “111”).
对于 one’s complement，我们只需要翻转所有位。 对于 2 的补码，我们首先找到 1 的补码。我们从 LSB （最低有效位）开始遍历 1 的补码，并查找 0。我们翻转所有 1（更改为 0），直到找到 0。最后，我们翻转找到的 0。例如，2 的补数 “01000” 是 “11000” （请注意，我们首先发现 01000 的补数是 10111）。 如果所有 1 （在 1 的补码中），我们在字符串中添加一个额外的 1。例如，2 的补码 “000” 是 “1000” （1 的补码 “000” 是 “111”）。

Below is the implementation.
下面是实现。

Try it on GfG Practice to print 1’s and 2’s complement of a binary number

输出二进制数的 1 和 2 的补码

C++

// C++ program to print 1's and 2's complement of
// a binary number
#include <bits/stdc++.h>
using namespace std;

// Returns '0' for '1' and '1' for '0'
char flip(char c) {return (c == '0')? '1': '0';}

// Print 1's and 2's complement of binary number
// represented by "bin"
void printOneAndTwosComplement(string bin)
{
int n = bin.length();
int i;

string ones, twos;
ones = twos = "";

// for ones complement flip every bit
for (i = 0; i < n; i++)
ones += flip(bin[i]);

// for two's complement go from right to left in
// ones complement and if we get 1 make, we make
// them 0 and keep going left when we get first
// 0, make that 1 and go out of loop
twos = ones;
for (i = n - 1; i >= 0; i--)
{
if (ones[i] == '1')
twos[i] = '0';
else
{
twos[i] = '1';
break;
}
}

// If No break : all are 1 as in 111 or 11111;
// in such case, add extra 1 at beginning
if (i == -1)
twos = '1' + twos;

cout << "1's complement: " << ones << endl;
cout << "2's complement: " << twos << endl;
}

// Driver program
int main()
{
string bin = "1100";
printOneAndTwosComplement(bin);
return 0;
}

Python3

# Python3 program to print 1's and 2's
# complement of a binary number

# Returns '0' for '1' and '1' for '0'
def flip(c):
return '1' if (c == '0') else '0'

# Print 1's and 2's complement of
# binary number represented by "bin"
def printOneAndTwosComplement(bin):

n = len(bin)
ones = ""
twos = ""

# for ones complement flip every bit
for i in range(n):
ones += flip(bin[i])

# for two's complement go from right
# to left in ones complement and if
# we get 1 make, we make them 0 and
# keep going left when we get first
# 0, make that 1 and go out of loop
ones = list(ones.strip(""))
twos = list(ones)
for i in range(n - 1, -1, -1):

if (ones[i] == '1'):
twos[i] = '0'
else:
twos[i] = '1'
break

i -= 1
# If No break : all are 1 as in 111 or 11111
# in such case, add extra 1 at beginning
if (i == -1):
twos.insert(0, '1')

print("1's complement: ", *ones, sep = "")
print("2's complement: ", *twos, sep = "")

# Driver Code
if __name__ == '__main__':
bin = "1100"
printOneAndTwosComplement(bin.strip(""))

# This code is contributed
# by SHUBHAMSINGH10

Javascript

<script>

// Javascript program to print 1's and 2's complement of
// a binary number

// Returns '0' for '1' and '1' for '0'
function flip (c) {return (c == '0')? '1': '0';}

// Print 1's and 2's complement of binary number
// represented by "bin"
function printOneAndTwosComplement(bin)
{
var n = bin.length;
var i;

var ones, twos;
ones = twos = "";

// for ones complement flip every bit
for (i = 0; i < n; i++)
ones += flip(bin[i]);

// for two's complement go from right to left in
// ones complement and if we get 1 make, we make
// them 0 and keep going left when we get first
// 0, make that 1 and go out of loop
twos = ones;
twos = twos.split('')
for (i = n - 1; i >= 0; i--)
{
if (ones[i] == '1')
twos[i] = '0';
else
{
twos[i] = '1';
break;
}
}
twos = twos.join('')
// If No break : all are 1 as in 111 or 11111;
// in such case, add extra 1 at beginning
if (i == -1)
twos = '1' + twos;

document.write( "1's complement: " + ones + "<br>");
document.write( "2's complement: " + twos + "<br>");
}

// Driver program
var bin = "1100";
printOneAndTwosComplement(bin);

</script>

-====

1’s补码和2’s补码计算

C++代码逻辑：

C++ 代码

// C++ program to print 1's and 2's complement of
// a binary number

#include <bits/stdc++.h>
using namespace std;

char flip(char c) { return (c == '0') ? '1' : '0'; }

void printOneAndTwosComplement(string bin) {
    int n = bin.length();
    string ones, twos;
    
    // 计算1's补码
    for (int i = 0; i < n; i++) {
        ones += flip(bin[i]);
    }
    
    // 计算2's补码
    twos = ones;
    for (int i = n - 1; i >= 0; i--) {
        if (ones[i] == '1 {
            twos[i] = '0';
        } else {
            twos[i] = '1';
            break;
        }
    }
    
    if (i == -1) {
        twos = '1' + twos;
    }
    
    cout << "1's complement: " << ones << endl;
    cout << "2's complement: " << twos << endl;
}

int main() {
    string bin = "1100";
    printOneAndTwosComplement(bin);
    return 0;
}

Python 代码

def flip(c):
    return '1' if c == '0' else '0'

def printOneAndTwosComplement(bin):
    n = len(bin)
    ones = []
    
    # 计算1's补码
    for c in bin:
        ones.append(flip(c))
    ones = ''.join(ones)
    
    # 计算2's补码
    twos = list(ones)
    for i in range(n-1, -1, -1):
        if ones[i] == '1':
            twos[i] = '0'
        else:
            twos[i] = '1'
            break
    else:
        twos.insert(0, '1')
    
    print("1's complement:", ones)
    print("2's complement:", ''.join(twos))

if __name__ == '__main__':
    bin = "1100"
    printOneAndTwosComplement(bin)

JavaScript 代码

function flip(c) { return (c == '0') ? '1' : '0'; }

function printOneAndTwosComplement(bin) {
    var n =.length;
    var ones = [];
    
    // 计算1's补码
    for (var = 0; i < n; i++) {
        ones.push(flip(bin[i]));
    }
    ones = ones.join('');
    
    // 计算2's补码
    var twos = ones.split('');
    for (var i = n - 1; i >= 0; i--) {
        if (ones[i] == '1') {
            twos[i] = '0';
        } else {
            twos[i] = '1';
            break;
        }
    }
    if (i == -1) {
        twos.unshift('1');
    }
    twos = twos.join('');
    
    document.write("1's complement " + ones + "<br>");
    document.write("2's complement: " + twos "<br>");
var bin = "1100";
printOneAndosComplement);

Output:
输出结果

1's complement: 0011
2's complement: 0100

1 补码: `0011`
2 补码 `0010`

Time Complexity: O(n)
时间复杂度：O(n)

Auxiliary Space: O(1)
辅助空间：O(1)

Thanks to Utkarsh Trivedi for the above solution.

As a side note, signed numbers generally use 2’s complement representation. Positive values are stored as it is and negative values are stored in their 2’s complement form. One extra bit is required to indicate whether the number is positive or negative. For example, char is 8 bits in C. If 2’s complement representation is used for char, then 127 is stored as it is, i.e., 01111111, where first 0 indicates positive. But -127 is stored as 10000001.

感谢 Utkarsh Trivedi 的上述解决方案。
作为补充说明，有符号数通常采用二进制补码表示。正数的存储方式与其二进制形式一致，而负数则以其二进制补码形式存储。为了指示数的正负，需要使用一个额外的位。例如，在 C 语言中，char 类型占用 8 位。如果采用二进制补码表示 char 类型，127 将被存储为 01111111，其中第一个 0 表示正数。而 - 127 则被存储为 10000001。

---

1的补码表示与2的补码表示技术之间的区别

Difference Between 1’s Complement Representation and 2’s Complement Representation Technique

1 的补码表示和 2 的补码表示技术之间的区别

Last Updated : 24 Sep, 2024

In computer science, binary number representations like 1’s complement and 2’s complement are essential for performing arithmetic operations and encoding negative numbers in digital systems. Understanding the differences between these two techniques is crucial for knowing how computers handle signed binary numbers. This article will explore the distinctions between 1’s complement and 2’s complement representations, their advantages and disadvantages, and their applications.
在计算机科学中，诸如1的补码和2的补码之类的二进制数表示法，对于在数字系统中执行算术运算以及对负数进行编码而言至关重要。理解这两种技术之间的差异，对于了解计算机如何处理有符号二进制数来说至关重要。本文将探究1的补码和2的补码表示之间的区别、它们的优缺点以及应用场景。

What is 1’s Complement?

什么是1的补码？

1’s complement of a binary number is another binary number obtained by toggling all bits in it, i.e., transforming the 0 bit to 1 and the 1 bit to 0. Example:
二进制数的1的补码是通过翻转其所有位而得到的另一个二进制数，即将0位变为1，1位变为0。示例：

Let numbers be stored using 4 bits
假设数字用4位存储

1's complement of 7 (0111) is 8 (1000)
7（0111）的1的补码是8（1000）
1's complement of 12 (1100) is 3 (0011)
12（1100）的1的补码是3（0011）

Advantages of 1’s Complement

1的补码优势

• Easy to compute by flipping bits.
  通过翻转位很容易计算。
• Suitable for basic arithmetic operations with a simpler hardware design.
  适用于硬件设计更简单的基本算术运算。

Disadvantages of 1’s Complement

1的补码的缺点

• 1’s complement has two representations of zero (0000 and 1111), which can cause complications in calculations.
  1的补码有两种零的表示形式（0000和1111），这可能会导致计算复杂化。
• Addition requires an end - around carry, which can complicate arithmetic operations.
  加法需要循环进位，这可能会使算术运算复杂化。
• Not as efficient in representing negative numbers compared to 2’s complement.
  与2的补码相比，在表示负数方面效率较低。

What is 2’s Complement?

什么是2的补码？

2’s complement is another binary number representation technique used widely in modern computers. To obtain the 2’s complement of a binary number, you invert all the bits (similar to 1’s complement) and add 1 to the least significant bit.
2的补码是现代计算机中广泛使用的另一种二进制数表示技术。要得到一个二进制数的2的补码，需先反转所有位（类似于1的补码），然后在最低有效位上加1。

2’s complement of a binary number is 1 added to the 1’s complement of the binary number. Examples:
二进制数的2的补码是该二进制数的1的补码加1。示例：

Let numbers be stored using 4 bits
假设数字用4位存储

2's complement of 7 (0111) is 9 (1001)
7（0111）的2的补码是9（1001）
2's complement of 12 (1100) is 4 (0100)
12（1100）的2的补码是4（0100）

Advantages of 2’s Complement

2的补码优势

• Only one representation of zero, which simplifies arithmetic operations.
  零只有一种表示形式，这简化了算术运算。
• No need for an end - around carry when adding numbers; subtraction can be done by adding the negative.
  相加时无需循环进位；减法可以通过加上负数来完成。
• Negative numbers have the most significant bit as 1, providing a clear distinction.
  负数的最高有效位为1，有明显的区分标志。

Disadvantages of 2’s Complement

2的补码的缺点

• Requires an additional step of adding 1 after inverting the bits.
  在反转位后需要额外进行加1的步骤。
• The range of negative numbers is one larger than the range of positive numbers, which can affect precision.
  负数的范围比正数的范围大1，这可能会影响精度。

These representations are used for signed numbers.
这些表示法用于有符号数。

The main difference between 1′ s complement and 2′ s complement is that 1′ s complement has two representations of 0 (zero) — 00000000, which is positive zero (+0), and 11111111, which is negative zero (-0); whereas in 2′ s complement, there is only one representation for zero — 00000000 (0) because if we add 1 to 11111111 (-1), we get 100000000, which is nine bits long. Since only eight bits are allowed, the left - most bit is discarded(or overflowed), leaving 00000000 (-0) which is the same as positive zero. This is the reason why 2′ s complement is generally used.
1’s补码和2’s补码之间的主要区别在于，1’s补码有两种0（零）的表示形式——00000000表示正零（+0），11111111表示负零（-0）；而在2’s补码中，零只有一种表示形式——00000000（0），因为如果我们给11111111（-1）加1，会得到100000000，这是9位长。由于只允许8位，最左边的位被丢弃（或溢出），剩下的00000000（-0）与正零相同。这就是通常使用2’s补码的原因。

Another difference is that while adding numbers using 1′ s complement, we first do binary addition, then add in an end - around carry value. But, 2′ s complement has only one value for zero and doesn’t require carry values.
另一个区别是，当使用1’s补码进行数字相加时，我们首先进行二进制加法，然后加上循环进位值。但是，2’s补码的零只有一种值，并且不需要进位值。

Range of 1’s complement for $n$ - bit number: $-(2^{n-1}-1)$ to $2^{n-1}-1$

$n$ 位 1 的补码的范围：$-(2^{n-1}-1)$ 到 $2^{n-1}-1$

Range of 2’s complement for $n$ - bit number: $-2^{n-1}$ to $2^{n-1}-1$

$n$ 位 2 的补码的范围：$-2^{n-1}$ 到 $2^{n-1}-1$

There are $2^{n-1}$ valid numbers in 1’s complement and $2^n$ valid numbers in 2’s complement.

1 的补码中有 $2^{n-1}$ 个有效数字，2 的补码中有 $2^n$ 个有效数字。

Difference Between 1’s Complement Representation and 2’s Complement Representation

1的补码表示和2的补码表示之间的区别

Feature 特征	1’s Complement 1的补码	2’s Complement 2的补码
Definition 定义	Inverts all bits of the binary number. 反转二进制数的所有位。	Inverts all bits and adds 1 to the least significant bit. 反转所有位，并将1添加到最低有效位。
Representation of Zero 零的表示	Two representations (0000 and 1111). 两种表示形式（0000和1111）。	One unique representation (0000). 一个唯一表示（0000）。
Negative Number Indication 负数指示	Most significant bit (MSB) is 1. 最高有效位（MSB）为1。	Most significant bit (MSB) is 1. 最高有效位（MSB）为1。
Arithmetic Operations 算术运算	Requires end - around carry during addition. 添加时需要循环进位。	No need for end - around carry, simplifying addition and subtraction. 无需循环进位，简化了加法和减法。
Range 范围	Symmetrical range; equal number of positive and negative values (e.g., -7 to +7). 对称范围；相等的正值和负值数（例如， -7到+7）。	Asymmetrical range; one more negative number than positive (e.g., -8 to +7). 不对称范围；负数比正数多一个（例如， -8到+7）。
Zero Value 零值	Has both +0 and -0. 同时具有+0和 -0。	Only one zero (0). 只有一个零（0）。
Complexity 复杂性	Easier to calculate (simple inversion). 更容易计算（简单反转）。	Slightly more complex (inversion plus adding 1). 稍微复杂一些（反转加1）。
Usage 用法	Rarely used in modern systems. 在现代系统中很少使用。	Widely used in modern computer systems. 广泛用于现代计算机系统。
Efficiency 效率	Less efficient due to double zero and end - around carry. 由于双零和循环进位，效率较低。	More efficient due to unique zero and simpler arithmetic operations. 由于唯一的零和更简单的算术运算，效率更高。
Overflow Handling 溢出处理	Can cause ambiguity due to double zero. 由于双零可能会导致歧义。	Clearly handled, with well - defined behavior. 处理清晰，行为明确。

Conclusion

结论

Both 1’s complement and 2’s complement techniques are crucial for binary arithmetic in computer systems. While 1’s complement is simpler to compute, it suffers from the drawback of double zero representation and the need for an end - around carry. In contrast, 2’s complement has become the standard in modern computing due to its efficient arithmetic operations, unique zero representation, and consistent handling of positive and negative values.
1的补码和2的补码技术对于计算机系统中的二进制算术运算都至关重要。虽然1的补码计算起来更简单，但它存在双零表示的缺点以及需要循环进位。相比之下，2的补码由于其高效的算术运算、唯一的零表示以及对正负值的一致处理，已成为现代计算中的标准。

Difference Between 1’s Complement Representation and 2’s Complement Representation Technique – FAQs

1 的补码表示和 2 的补码表示技术之间的区别 – 常见问题解答

Why is 2’s complement preferred over 1’s complement?

为什么2的补码比1的补码更受青睐？

2’s complement is preferred because it simplifies arithmetic operations and provides a unique representation for zero, avoiding complications associated with 1’s complement.
2的补码更受青睐，因为它简化了算术运算，并为零提供了唯一的表示形式，避免了与1的补码相关的复杂性。

*How do you find the 1’s complement and 2’s complement of a binary number?

如何求一个二进制数的 1 的补码和 2 的补码？

To find the 1’s complement, invert all the bits. For 2’s complement, invert all the bits and add 1 to the result.
要找到 1 的补码，反转所有位。对于 2 的补码，反转所有位并将结果加 1。

What are the limitations of using 1’s complement?

使用 1 的补码有哪些限制？

The primary limitations include the double representation of zero and the need for an end - around carry during addition, which complicates arithmetic operations.
主要限制包括零的双重表示以及加法时需要循环进位，这使算术运算变得复杂。

Does 2’s complement have any disadvantages?

2 的补码有什么缺点吗？

The main disadvantage is the asymmetry in the range of positive and negative numbers, as the range of negative numbers is one larger.
主要缺点是正数和负数范围的不对称性，因为负数的范围大 1。

---

Signed Binary Numbers

有符号二进制数

Signed Binary Numbers use the MSB as a sign bit to display a range of either positive numbers or negative numbers
有符号二进制数使用 MSB 作为符号位来显示正数或负数的范围

In mathematics, positive numbers (including zero) are represented as unsigned numbers. That is we do not put the +ve sign in front of them to show that they are positive numbers. But when dealing with negative numbers we do use a -ve sign in front of the number to show that the number is negative in value and different from a positive unsigned value, and the same is true with signed binary numbers.
在数学中，正数（包括零）表示为无符号数。也就是说，我们不会在它们前面加上 +ve 符号来表明它们是正数。但是在处理负数时，我们确实在数字前面使用 -ve 符号来表示该数字是负值并且不同于正的无符号值，有符号二进制数也是如此。

However, in digital circuits there is no provision made to put a plus or even a minus sign to a number, since digital systems operate with binary numbers that are represented in terms of “0’s” and “1’s”. When used together in microelectronics, these “1’s” and “0’s”, called a bit (being a contraction of BInary digiT), fall into several range sizes of numbers which are referred to by common names, such as a byte or a word.
然而，在数字电路中，没有规定在数字上加上加号甚至减号，因为数字系统使用以“0”和“1”表示的二进制数。当在微电子学中一起使用时，这些“1”和“0”称为位（是 BInary digiT 的缩写），分为几个数字范围大小，这些数字由通用名称（例如字节或单词）表示。

We have also seen previously that an 8-bit binary number (a byte) can have a value ranging from 0 (00000000_2) to 255 (11111111_2), that is 28 = 256 different combinations of bits forming a single 8-bit byte. So for example an unsigned binary number such as: 010011012 = 64 + 8 + 4 + 1 = 7710 in decimal. But Digital Systems and computers must also be able to use and to manipulate negative numbers as well as positive numbers.
我们之前还看到，一个 8 位二进制数（一个字节）的值可以从 0 （00000000_2） 到 255 （11111111_2），即 28 = 256 个不同的位组合形成一个 8 位字节。例如，一个无符号的二进制数，例如：010011012 = 64 + 8 + 4 + 1 = 7710（十进制）。但是 Digital Systems 和计算机也必须能够使用和纵负数和正数。

Mathematical numbers are generally made up of a sign and a value (magnitude) in which the sign indicates whether the number is positive, ( + ) or negative, ( – ) with the value indicating the size of the number, for example 23, +156 or -274. Presenting numbers is this fashion is called “sign-magnitude” representation since the left most digit can be used to indicate the sign and the remaining digits the magnitude or value of the number.
数学数字通常由一个符号和一个值（大小）组成，其中符号表示数字是正数、（ + ） 还是负数 （ – ），值表示数字的大小，例如 23、+156 或 -274。表示数字的方式称为“符号-幅度”表示，因为最左边的数字可用于表示符号，其余数字表示数字的大小或值。

Sign-magnitude notation is the simplest and one of the most common methods of representing positive and negative numbers either side of zero, (0). Thus negative numbers are obtained simply by changing the sign of the corresponding positive number as each positive or unsigned number will have a signed opposite, for example, +2 and -2, +10 and -10, etc.
符号幅度表示法是表示零 （0） 两侧的正数和负数的最简单也是最常用的方法之一。因此，只需更改相应正数的符号即可获得负数，因为每个正数或无符号数都会有一个有符号的对立面，例如 +2 和 -2、+10 和 -10 等。

But how do we represent signed binary numbers if all we have is a bunch of one’s and zero’s. We know that binary digits, or bits only have two values, either a “1” or a “0” and conveniently for us, a sign also has only two values, being a “+” or a “–“.
但是，如果我们所拥有的只是一堆 1 和 0，我们如何表示有符号的二进制数呢？我们知道二进制数字或位只有两个值，要么是“1”，要么是“0”，对我们来说很方便，一个符号也只有两个值，即“+”或“-”。

Then we can use a single bit to identify the sign of a signed binary number as being positive or negative in value. So to represent a positive binary number (+n) and a negative (-n) binary number, we can use them with the addition of a sign.
然后我们可以使用单个位来识别有符号二进制数的符号是正值还是负值。因此，要表示正二进制数 （+n） 和负 （-n） 二进制数，我们可以在使用它们时加上一个符号。

For signed binary numbers the most significant bit (MSB) is used as the sign bit. If the sign bit is “0”, this means the number is positive in value. If the sign bit is “1”, then the number is negative in value. The remaining bits in the number are used to represent the magnitude of the binary number in the usual unsigned binary number format way.
对于有符号二进制数，最高有效位 （MSB） 用作符号位。如果符号位为 “0”，则表示该数字为正值。如果符号位为 “1”，则数字为负值。数字中的其余位用于以通常的无符号二进制数格式方式表示二进制数的大小。

Then we can see that the Sign-and-Magnitude (SM) notation stores positive and negative values by dividing the “n” total bits into two parts: 1 bit for the sign and n–1 bits for the value which is a pure binary number. For example, the decimal number 53 can be expressed as an 8-bit signed binary number as follows.
然后我们可以看到，符号和幅度 （SM） 表示法通过将“n”个总位分为两部分来存储正值和负值：1 位用于符号，n-1 位用于纯二进制数的值。例如，十进制数 53 可以表示为 8 位有符号二进制数，如下所示。

Positive Signed Binary Numbers

正有符号二进制数

Negative Signed Binary Numbers

负有符号二进制数

The disadvantage here is that whereas before we had a full range n-bit unsigned binary number, we now have an n-1 bit signed binary number giving a reduced range of digits from:
这里的缺点是，以前我们有一个全范围的 n 位无符号二进制数，而现在我们有一个 n-1 位有符号二进制数，给出了缩小的数字范围：

-2^(n-1)  to  +2^(n-1)

So for example: if we have 4 bits to represent a signed binary number, (1-bit for the Sign bit and 3-bits for the Magnitude bits), then the actual range of numbers we can represent in sign-magnitude notation would be:
例如：如果我们有 4 位来表示有符号二进制数（1 位表示 Sign 位，3 位表示 Magnitude 位），那么我们可以用 sign-magnitude 表示法表示的数字的实际范围为：

$$\begin{array}{rl}-2^{(4-1)}-1& \text{ to }+2^{(4-1)}-1\\ -2^{(3)}-1& \text{ to }+2^{(3)}-1\\ -7& \text{ to }+7\end{array}$$

Whereas before, the range of an unsigned 4-bit binary number would have been from 0 to 15, or 0 to F in hexadecimal, we now have a reduced range of -7 to +7. Thus an unsigned binary number does not have a single sign-bit, and therefore can have a larger binary range as the most significant bit (MSB) is just an extra bit or digit rather than a used sign bit.
以前，无符号 4 位二进制数的范围是从 0 到 15，或者十六进制的 0 到 F，而现在我们的范围缩小到 -7 到 +7。因此，无符号二进制数没有单个符号位，因此可以具有更大的二进制范围，因为最高有效位 （MSB） 只是一个额外的位或数字，而不是一个使用的符号位。

Another disadvantage here of the sign-magnitude form is that we can have a positive result for zero, +0 or 0000_2, and a negative result for zero, -0 or 1000_2. Both are valid but which one is correct.
符号大小形式的另一个缺点是，我们可以得到 0、+0 或 0000_2 的正结果，以及 0、-0 或 1000_2 的负结果。两者都是有效的，但哪一个是正确的。

Signed Binary Numbers Example No1

有符号二进制数示例 No1

Convert the following decimal values into signed binary numbers using the sign-magnitude format:
使用 sign-magnitude 格式将以下十进制值转换为有符号的二进制数：

-15_10 as a 6-bit number	⇒	101111_2
+23_10 as a 6-bit number	⇒	010111_2
-56_10 as a 8-bit number	⇒	10111000_2
+85_10 as a 8-bit number	⇒	01010101_2
-127_10 as a 8-bit number	⇒	11111111_2

Note that for a 4-bit, 6-bit, 8-bit, 16-bit or 32-bit signed binary number all the bits MUST have a value, therefore “0’s” are used to fill the spaces between the leftmost sign bit and the first or highest value “1”.
请注意，对于 4 位、6 位、8 位、16 位或 32 位有符号二进制数，所有位都必须有一个值，因此 “0” 用于填充最左边的符号位和第一个或最高值 “1” 之间的空格。

The sign-magnitude representation of a binary number is a simple method to use and understand for representing signed binary numbers, as we use this system all the time with normal decimal (base 10) numbers in mathematics. Adding a “1” to the front of it if the binary number is negative and a “0” if it is positive.
二进制数的符号幅度表示是一种用于表示有符号二进制数的简单方法，因为我们在数学中一直使用该系统来表示正常的十进制（以 10 为基数）。如果二进制数为负数，则在其前面添加 “1”，如果二进制数为正，则在其前面添加 “0”。

However, using this sign-magnitude method can result in the possibility of two different bit patterns having the same binary value. For example, +0 and -0 would be 0000 and 1000 respectively as a signed 4-bit binary number.
但是，使用这种符号幅度方法可能会导致两个不同的 bit patterns 具有相同的 binary 值。例如，+0 和 -0 将分别是 0000 和 1000 作为有符号的 4 位二进制数。

So we can see that using this method there can be two representations for zero, a positive zero ( 0000_2 ) and also a negative zero ( 10002 ) which can cause big complications for computers and digital systems.
所以我们可以看到，使用这种方法，零可以有两种表示形式，一个正零 （ 0000_2 ） 和一个负零 （ 1000_2 ），这可能会给计算机和数字系统带来很大的复杂性。

One’s Complement of a Signed Binary Number

1 的有符号二进制数的补码

One’s Complement or 1’s Complement as it is also termed, is another method which we can use to represent negative binary numbers in a signed binary number system. In one’s complement, positive numbers (also known as non-complements) remain unchanged as before with the sign-magnitude numbers.
One’s Complement 或 1’s Complement 也被称为 1’s Complement，是我们可以用来在有符号二进制数系统中表示负二进制数的另一种方法。在 1 的补码中，正数（也称为非补码）与符号大小数一样保持不变。

Negative numbers however, are represented by taking the one’s complement (inversion, negation) of the unsigned positive number. Since positive numbers always start with a “0”, the complement will always start with a “1” to indicate a negative number.
然而，负数是通过取无符号正数的 1 的补码（反转、否定）来表示的。由于正数总是以 “0” 开头，因此补码将始终以 “1” 开头以表示负数。

The one’s complement of a negative binary number is the complement of its positive counterpart, so to take the one’s complement of a binary number, all we need to do is change each bit in turn. Thus the one’s complement of “1” is “0” and vice versa, then the one’s complement of 10010100_ is simply 01101011_2 as all the 1’s are changed to 0’s and the 0’s to 1’s.
负二进制数的 1 补数是其正对应物的补码，因此要取二进制数的 1 补码，我们需要做的就是依次更改每个位。因此，1 的补数 “1” 是 “0”，反之亦然，那么 1 的补数 10010100_2 就是 01101011_2，因为所有的 1 都变成了 0,0 变成了 1。

The easiest way to find the one’s complement of a signed binary number when building digital arithmetic or logic decoder circuits is to use Inverters. The inverter is naturally a complement generator and can be used in parallel to find the 1’s complement of any binary number as shown.
在构建数字算术或逻辑解码器电路时，找到有符号二进制数的 1 补码的最简单方法是使用 Inverters。反相器自然是一个补码生成器，可以并联使用以查找任何二进制数的 1 补码，如图所示。

1’s Complement Using Inverters

使用反相器的 1 的补充

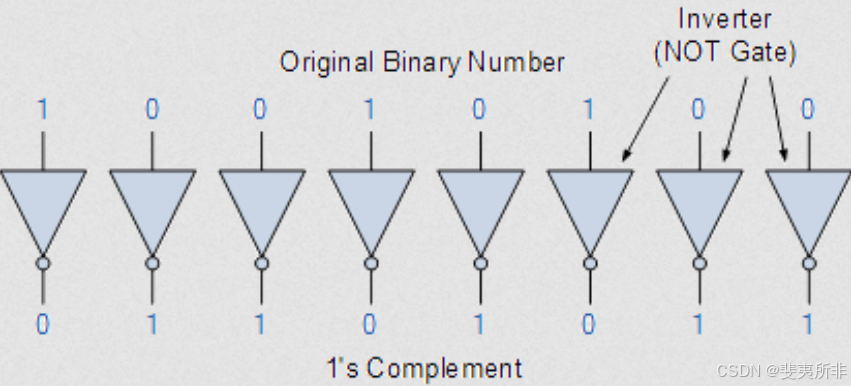
Then we can see that it is very easy to find the one’s complement of a binary number N as all we need do is simply change the 1’s to 0’s and the 0’s to 1’s to give us a -N equivalent. Also just like the previous sign-magnitude representation, one’s complement can also have n-bit notation to represent numbers in the range from: -2^(n-1) and +2^(n-1) – 1.
然后我们可以看到，找到二进制数 N 的 1 补码非常容易，因为我们需要做的就是简单地将 1 改为 0，将 0 改为 1，从而得到 -N 等价物。就像前面的符号大小表示一样，一个人的补码也可以有 n 位表示法来表示 -2^(n-1) 和 +2^(n-1) – 1. 范围内的数字。

For example, a 4-bit representation in the one’s complement format can be used to represent decimal numbers in the range from -7 to +7 with two representations of zero: 0000 (+0) and 1111 (-0) the same as before.
例如，1 的补码格式的 4 位表示形式可用于表示 -7 到 +7 范围内的十进制数，其中两种零表示形式：0000 （+0） 和 1111 （-0） 与以前相同。

Addition and Subtraction Using One’s Complement

使用 1 的补码进行加法和减法

One of the main advantages of One’s Complement is in the addition and subtraction of two binary numbers. In mathematics, subtraction can be implemented in a variety of different ways as A – B, is the same as saying A + (-B) or -B + A etc. Therefore, the complication of subtracting two binary numbers can be performed by simply using addition.
One’s Complement 的主要优点之一是两个二进制数的加法和减法。在数学中，减法可以通过多种不同的方式实现，如 A – B，与说 A + （-B） 或 -B + A 等相同。因此，减去两个二进制数的复杂功能可以通过简单地使用加法来完成。

We saw in the Binary Adder tutorial that binary addition follows the same rules as for the normal addition except that in binary there are only two bits (digits) and the largest digit is a “1”, (just as “9” is the largest decimal digit) thus the possible combinations for binary addition are as follows:
我们在 二进制加法器 中看到，二进制加法遵循与正常加法相同的规则，只是在二进制中只有两个位（数字），最大数字是 “1” （就像 “9” 是最大的十进制数字一样），因此二进制加法的可能组合如下：

0	0	1	1
+ 0	+ 1	+ 0	+ 1
0	1	1	1← 0	( 0 plus a carry 1 )

When the two numbers to be added are both positive, the sum A + B, they can be added together by means of the direct sum (including the number and bit sign), because when single bits are added together, “0 + 0”, “0 + 1”, or “1 + 0” results in a sum of “0” or “1”.
当两个数字相加都是正数时，即总和A + B，可以通过直接求和（包括数字和位号）的方式将它们相加，因为当单个位相加时，“0 + 0”、“0 + 1”或“1 + 0”会得到“0”或“1”之和。

This is because when the two bits we want to be added together are odd (“0” + “1” or “1 + 0”), the result is “1”. Likewise when the two bits to be added together are even (“0 + 0” or “1 + 1”) the result is “0” until you get to “1 + 1” then the sum is equal to “0” plus a carry “1”. Let’s look at a simple example.
这是因为当我们要加在一起的两个位是奇数（“0” + “1” 或 “1 + 0”）时，结果是 “1”。同样，当要加在一起的两个位是偶数（“0 + 0”或“1 + 1”）时，结果是“0”，直到你得到“1 + 1”，然后和等于“0”加上进位“1”。让我们看一个简单的例子。

Subtraction of Two Binary Numbers

两个二进制数的减法

An 8-bit digital system is required to subtract the following two numbers 115 and 27 from each other using one’s complement. So in decimal this would be: 115 – 27 = 88.
需要一个 8 位数字系统来使用补码将以下两个数字 115 和 27 相互减去。所以以十进制为单位，这将是：115 – 27 = 88。

First we need to convert the two decimal numbers into binary and make sure that each number has the same number of bits by adding leading zero’s to produce an 8-bit number (byte). Therefore:
首先，我们需要将两个十进制数转换为二进制，并通过添加前导零来生成 8 位数字（字节），确保每个数字具有相同的位数。因此：

115₁₀ in binary is: 01110011₂
27₁₀ in binary is: 00011011₂

Now we need to find the complement of the second binary number, (00011011) while leaving the first number (01110011) unchanged. So by changing all the 1’s to 0’s and 0’s to 1’s, the one’s complement of 00011011 is therefore equal to 11100100.
现在我们需要找到第二个二进制数 （00011011） 的补数，同时保持第一个数字 （01110011） 不变。因此，通过将所有 1 更改为 0，将 0 更改为 1,00011011 的 1 补数等于 11100100。

Adding the first number and the complement of the second number gives:
将第一个数字和第二个数字的补码相加得到：

	01110011
	+ 11100100
Overflow	→ 1 01010111

Since the digital system is to work with 8-bits, only the first eight digits are used to provide the answer to the sum, and we simply ignore the last bit (bit 9). This bit is call an “overflow” bit. Overflow occurs when the sum of the most significant (left-most) column produces a carry forward. This overflow or carry bit can be ignored completely or passed to the next digital section for use in its calculations. Overflow indicates that the answer is positive. If there is no overflow then the answer is negative.
由于数字系统要使用 8 位，因此仅使用前 8 位数字来提供和的答案，我们只需忽略最后一位（第 9 位）。此位称为 “overflow” 位。当最有效（最左侧）列的总和产生结转时，将发生溢出。这个 overflow 或 carry bit 可以完全忽略，也可以传递给下一个 digital 部分用于其计算。Overflow 表示答案为肯定。如果没有溢出，则答案是否定的。

The 8-bit result from above is: 01010111 (the overflow “1” cancels out) and to convert it back from a one’s complement answer to the real answer we now have to add “1” to the one’s complement result, therefore:
上面的 8 位结果是：01010111（溢出的 “1” 抵消），要将其从 1 的补码答案转换回真正的答案，我们现在必须在 1 的补码结果中添加 “1”，因此：

01010111
+ 1
01011000

So the result of subtracting 27 ( 00011011_2 ) from 115 ( 01110011_2 ) using 1’s complement in binary gives the answer of: 01011000_2 or (64 + 16 + 8) = 88_10 in decimal.
因此，使用 1 的二进制补码从 115 （ 01110011_2 ） 中减去 27 （ 00011011_2 ） 的结果给出了答案：01011000_2 或 （64 + 16 + 8） = 88_10 十进制。

Then we can see that signed or unsigned binary numbers can be subtracted from each other using One’s Complement and the process of addition. Binary adders such as the TTL 74LS83 or 74LS283 can be used to add or subtract two 4-bit signed binary numbers or cascaded together to produce 8-bit adders complete with carry-out.
然后我们可以看到，有符号或无符号的二进制数可以使用 1 的补码和加法过程相互减去。二进制加法器（如 TTL 74LS83 或 74LS283）可用于加减两个 4 位有符号二进制数，或级联在一起以产生 8 位加法器，并带有进出功能。

Two’s Complement

2 的补码

Two’s Complement or 2’s Complement as it is also termed, is another method like the previous sign-magnitude and one’s complement form, which we can use to represent negative binary numbers in a signed binary number system. In two’s complement, the positive numbers are exactly the same as before for unsigned binary numbers. A negative number, however, is represented by a binary number, which when added to its corresponding positive equivalent results in zero.
2’s Complement 或 2’s Complement 也被称为 2’s Complement，是另一种方法，就像前面的符号幅度和 1 的补码形式一样，我们可以用它来表示有符号二进制数系统中的负二进制数。在 2 的补码中，正数与以前对于无符号二进制数完全相同。但是，负数由二进制数表示，当二进制数与相应的正等效数相加时，结果为零。

In two’s complement form, a negative number is the 2’s complement of its positive number with the subtraction of two numbers being A – B = A + ( 2’s complement of B ) using much the same process as before as basically, two’s complement is one’s complement + 1.
在 2 的补码形式中，负数是其正数的 2 补码，两个数的减法是 A – B = A + （ 2 的 B 补码），使用与以前大致相同的过程，基本上，2 的补码是 1 的补码 + 1。

The main advantage of two’s complement over the previous one’s complement is that there is no double-zero problem plus it is a lot easier to generate the two’s complement of a signed binary number. Therefore, arithmetic operations are relatively easier to perform when the numbers are represented in the two’s complement format.
2 的补码相对于前一个的补码的主要优点是没有双零问题，而且生成有符号二进制数的 2 补码要容易得多。因此，当数字以 2 的补码格式表示时，算术运算相对容易执行。

Let’s look at the subtraction of our two 8-bit numbers 115 and 27 from above using two’s complement, and we remember from above that the binary equivalents are:
让我们看看使用二进制补码将两个 8 位数字 115 和 27 从上面减去，我们从上面记住二进制等价物是：

115₁₀ in binary is: 01110011₂

27₁₀ in binary is: 00011011₂

Our numbers are 8-bits long, then there are 2^8 digits available to represent our values and in binary this equals: 100000000_2 or 256_10. Then the two’s complement of 2710 will be:
我们的数字是 8 位长，然后有 2^8 位数字可以代表我们的值，二进制等于：100000000_2 或 256_10。那么 2710 的补数将是：

$(2^8{)}_2–00011011=100000000–00011011=11100101_2$

The complementation of the second negative number means that the subtraction becomes a much easier addition of the two numbers so therefore the sum is: 115 + ( 2’s complement of 27 ) which is:
第二个负数的补数意味着减法变得更容易将两个数字相加，因此总和为：115 + （ 2 的补数 27 ），即：

01110011 + 11100101 = 1 010110002

As previously, the 9th overflow bit is disregarded as we are only interested in the first 8-bits, so the result is: 01011000_2 or (64 + 16 + 8) = 88_10 in decimal the same as before.
和以前一样，第 9 个溢出位被忽略，因为我们只对前 8 位感兴趣，所以结果是：010110002 或 （64 + 16 + 8） = 88_10，十进制和以前一样。

Tutorial Summary

教程摘要

We have seen that negative binary numbers can be represented by using the most significant bit (MSB) as a sign bit. If an n bit binary number is signed the leftmost bit is used to represent the sign leaving n-1 bits to represent the number.
我们已经看到，负二进制数可以通过使用最高有效位 （MSB） 作为符号位来表示。如果 n 位二进制数有符号，则使用最左边的位表示符号，留下 n-1 位来表示数字。

For example, in a 4-bit binary number, this leaves only 3 bits to hold the actual number. If however, the binary number is unsigned then all the bits can be used to represent the number.
例如，在 4 位二进制数中，只剩下 3 位来保存实际数字。但是，如果二进制数是无符号的，则所有位都可用于表示该数字。

The representation of a signed binary number is commonly referred to as the sign-magnitude notation and if the sign bit is “0”, the number is positive. If the sign bit is “1”, then the number is negative. When dealing with binary arithmetic operations, it is more convenient to use the complement of the negative number.
有符号二进制数的表示通常称为符号幅度表示法，如果符号位为“0”，则数字为正数。如果符号位为 “1”，则数字为负数。在处理二进制算术运算时，使用负数的补码更方便。

Complementation is an alternative way of representing negative binary numbers. This alternative coding system allows for the subtraction of negative numbers by using simple addition.
互补是表示负二进制数的另一种方式。这种替代编码系统允许使用简单的加法来减去负数。

Since positive sign-magnitude numbers always start with a zero (0), its complement will therefore always start with a one (1) to indicate a negative number as shown in the following table.
由于正符号幅度数总是以零 （0） 开头，因此其补码将始终以一 （1） 开头以表示负数，如下表所示。

4-bit Signed Binary Number Comparison

4 位有符号二进制数比较

Decimal	Signed Magnitude	Signed One’s Complement	Signed Two’s Complement
+7	0111	0111	0111
+6	0110	0110	0110
+5	0101	0101	0101
+4	0100	0100	0100
+3	0011	0011	0011
+2	0010	0010	0010
+1	0001	0001	0001
+0	0000	0000	0000
-0	1000	1111	–
-1	1001	1110	1111
-2	1010	1101	1110
-3	1011	1100	1101
-4	1100	1011	1100
-5	1101	1010	1011
-6	1110	1001	1010
-7	1111	1000	1001

Signed-complement forms of binary numbers can use either 1’s complement or 2’s complement. The 1’s complement and the 2’s complement of a binary number are important because they permit the representation of negative numbers.
二进制数的符号补码形式可以使用 1 的补码或 2 的补码。二进制数的 1 的补码和 2 的补码很重要，因为它们允许表示负数。

The method of 2’s complement arithmetic is commonly used in computers to handle negative numbers the only disadvantage is that if we want to represent negative binary numbers in the signed binary number format, we must give up some of the range of the positive number we had before.
2 的补码算术方法在计算机中常用于处理负数，唯一的缺点是，如果我们想用有符号的二进制数格式表示负二进制数，我们必须放弃我们之前拥有的正数的一些范围。

---

One’s and Two’s Complement of Binary Number

二进制数的反码和补码

The article provides a general overview of essential mathematical operations on binary numbers, focusing on addition, subtraction, and the formation of negative binary numbers. Additionally, it introduces concepts like one’s complement, two’s complement, and multiplication/division of unsigned binary numbers, with practical examples and insights into their application in microprocessors.
本文全面概述了二进制数的基本数学运算，重点聚焦于加法、减法以及负二进制数的构成方式。此外，还介绍了反码、补码的概念，以及无符号二进制数的乘法和除法运算，并通过实际示例阐述了它们在微处理器中的应用。

For the analysis of practical applications, it is necessary to do mathematical operations on binary numbers. This is the basis of all that a microprocessor does. In this section, we study how two binary numbers are added, and how one is subtracted from the other. We also discuss how the negative of a binary number is formed.
在实际应用分析中，对二进制数进行数学运算是必要的。这是微处理器所有运算的基础。在本节中，我们将学习两个二进制数如何相加、如何相减，同时还会探讨如何得到一个二进制数的负数形式。

Addition of Two Binary Numbers

两个二进制数的加法

The addition of two binary numbers is performed in the same way as we add two decimal numbers with the exception that the only nonzero element in the set of basic elements of the binary number system is the number 1. Thus, in the same way, that in decimal numbers if we add 1 to 9, the answer is 10, in binary numbers if we add 1 to 1, the answer is 10. That is, the addition of 1 and 1 is a 0 with a 1 carried over to the next digit on the left. Also, practically, which is the way this operation is performed in microprocessors, only two numbers are added together at a time. We consider the following three examples. Assume unsigned numbers.
两个二进制数的加法运算方式与十进制数加法类似，区别在于二进制数系统的基本元素中，唯一的非零元素是 1。所以，就像在十进制中 1 加 9 等于 10 一样，在二进制里 1 加 1 等于 10。也就是说，1 加 1 的结果是本位为 0，向左边的下一位进位 1。实际上，在微处理器中，每次只对两个数进行相加运算。以下是三个无符号数相加的例子。

Because any binary numbers are practically the contents of a register, only a limited number of bits are available. This is because of the hardware, which determines the bit size to be 8, 10, 12, or some other.
由于任何二进制数实际上都是寄存器中的内容，受硬件限制，可用的位数是有限的，通常为 8 位、10 位、12 位或其他特定的位数。

In the result of adding two numbers, you see that the very last digit on the left is shown in red when it happens to exist. This digit (bit) is ignored. There is physically no place for this bit to go to. It is either not significant (in a subtraction operation, as you will see next), or it is an indication of overflow (as shown above).
在两个数相加的结果中，如果最左边的最后一位存在，会用红色显示。这一位（比特）会被忽略，因为在物理层面它没有存储的位置。它要么在减法运算中没有意义（接下来你会看到），要么表示溢出（如上述示例）。

Overflow is a situation where a number is larger than the capacity of the machine. When there is an overflow situation, the last bit is ignored, but it signals out a flag.
溢出指的是数字超出了机器的表示范围。当发生溢出时，最后一位会被忽略，但会触发一个标志位。

A flag is an indicator of an undesirable or fault situation in digital systems. A message will be issued when a flag is signaled. An example is when you have a division by zero in your calculator.
标志位是数字系统中异常或错误情况的指示器。当标志位被触发时，系统会发出提示信息，比如计算器中出现除零错误时。

Overflow
State of reaching a value beyond the capacity of a
digital device in terms of the number of bits.
在数字设备中，由于位数限制，数字达到超出设备表示能力的值的状态。
 
Flag
Representation of the occurrence of some unusual or
unwanted situation in digital circuits and computer terminology.
在数字电路和计算机术语中，用于表示某些异常或不期望情况发生的标识。

Subtraction of Two Binary Numbers

两个二进制数的减法

To subtract a number B from number A the common method is to add A to the negative of B.
从数 A 中减去数 B，常用的方法是将 A 与 B 的负数相加。
$A-B=A+(-B)$

The subtraction, then, changes to an addition operation. Then, in the same way, as discussed above the two numbers are added.
这样，减法运算就转变为加法运算。然后，按照上述加法的方式对这两个数进行相加。

Consider for example subtraction of 44 (0010, 1100b) from 108 (0110, 1100b) in binary operation. Instead, we add −44 (1101, 0100b) to 108
例如，在二进制运算中，要从 108（二进制表示为 0110, 1100₂）中减去 44（二进制表示为 0010, 1100₂），我们可以将 -44（二进制表示为 1101, 0100₂）与 108 相加。

You can easily check that 108 − 44 = 64, and the resultant binary number (0100, 0000b) is 64. Also, you can verify the number for −44 to be correct. If it is added to 44, the resultant is 0.
可以很容易验证，108 - 44 = 64，结果的二进制数（0100, 0000₂）确实表示 64。同时，也能验证 -44 的二进制表示是正确的，因为 -44 与 44 相加结果为 0。

Note that in both cases the very last digit, shown in red, does not play any role and is ignored.
注意，在这两种情况下，最左边的最后一位（红色显示）不参与运算，会被忽略。

One’s Complement of a Binary Number

二进制数的反码

The one’s complement of a binary number is used to find the two’s complement of a number, which is used to find the negative of that number. Note that negatives are valid with signed numbers.
二进制数的反码用于求该数的补码，而补码用于表示该数的负数形式。需要注意的是，负数只有在有符号数中才有意义。

The one’s complement of a number is obtained by switching each bit to its opposite value, 1’s to 0’s and 0’s to 1’s. For example, the one’s complement of 0110, 1010 (106) is 1001, 0101.
一个数的反码是通过将每一位取反得到的，即将 1 变为 0，0 变为 1。例如，0110, 1010（十进制为 106）的反码是 1001, 0101。

One’s complement
The result of swapping each bit value to its
complement in a binary number.
将二进制数中的每一位取反后得到的结果。
 
Two’s complement
A binary number obtained by adding 1 to the one’s
complement of a binary number.
在二进制数的反码上加 1 得到的数。

Two’s Complement of a Binary Number

二进制数的补码

Two’s complement of a binary number is obtained by adding 1 to the one’s complement of that number. For instance,
二进制数的补码是在其反码的基础上加 1 得到的。例如，

if one’s complement of a number is 10010101 then the two’s complement of it is
如果一个数的反码是 10010101，那么它的补码为：

The two’s complement defines the negative of a number. Therefore, the negative of 0110, 1010b is 1001, 0110b. We can check this by adding the two numbers together.
补码用于定义一个数的负数形式。因此，0110, 1010₂的负数是 1001, 0110₂。我们可以通过将这两个数相加来验证。

$$\begin{array}{c}01101010+\\ 10010110\\ ——\\ 100000000\end{array}$$

One’s and Two’s Complement Example

反码和补码示例

Find the negative of the binary number 1110, 0111.
求二进制数 1110, 0111 的负数。

Solution
解答

First, note that this number is already negative because its most significant bit is 1. The negative of a negative number is positive. No matter if the number is initially positive or negative, the two steps to be taken are
首先，注意到这个数的最高位是 1，所以它本身是一个负数，负数的负数是正数。无论初始数字是正数还是负数，都需要进行以下两个步骤：

Step 1: Find the one’s complement of the number One’s complement of 1110, 0111 is 0001, 1000.
步骤 1：求该数的反码。1110, 0111 的反码是 0001, 1000。

Step 2: Find the two’s complement of the number (or, add 1 to the one’s complement)
步骤 2：求该数的补码（即反码加 1）
$\text{0001,100}{\text{0}}_{\text{b}}\text{ + 1 = 0001,100}{\text{1}}_{\text{b}}$
The answer, thus, is 0001, 1001. Verifying the result:
所以，答案是 0001, 1001。验证结果：

$$\begin{array}{c}11100111+\\ 00011001\\ ——\\ 100000000\end{array}$$

The given numbers was −25. You cannot say that easily just from the number directly by looking at the digits, except that one has a look-up table showing all the numbers in the range.
给定的数 1110, 0111 表示 -25。如果没有查找表，很难直接从数字的二进制表示判断其十进制值。

Figure 1 shows some numbers between −128 and −1. You may notice a pattern to determine the numbers for 8 bits as shown in the table. On the basis of this pattern, find the decimal magnitude of the binary number leaving out the leftmost bit, and subtract 128 from that number. For other bit numbers, the value to subtract (128 in this case) must be changed accordingly.
图 1 展示了 -128 到 -1 之间的一些 8 位二进制数。可以发现一个规律：对于 8 位二进制数，去掉最左边的符号位后，将剩余数字转换为十进制，再减去 128，就可以得到该二进制数表示的十进制值。对于其他位数的二进制数，需要相应调整减去的值（此处为 128）。

Represents a negative number
表示负数

Figure 1 Negative binary numbers.
图 1：负二进制数

The two’s complement of a binary number defines the negative of that number.
二进制数的补码定义了该数的负数形式。

Multiplication and Division of Unsigned Binary Numbers

无符号二进制数的乘法和除法

Multiplication of binary numbers is very easy. This is the way multiplication is performed in a microprocessor. First, consider multiplication by 10b and 100b, which is, in fact, multiplication by 2 and 4. Consider 0011, 1011b (always assume a limited number of bits, here 8). Assume an unsigned number.
二进制数的乘法运算很简单，这也是微处理器中乘法运算的实现方式。首先，考虑乘以 10₂和 100₂的情况，实际上这分别相当于乘以 2 和 4。以 0011, 1011₂（假设为 8 位无符号数）为例：

$$\begin{array}{rl}& \begin{array}{ccc}0011,{1011}_b\times {10}_b=0111,{1011}_b& & \left(59\times 2=118\right)\end{array}\\ & \begin{array}{ccc}0011,{1011}_b\times {100}_b=1110,{1011}_b& & \left(59\times 4=236\right)\end{array}\end{array}$$

As in the case of decimal numbers 1 or 2, 0’s are added to the right side of the number for multiplication by 10b and 100b, respectively. Because the number of bits must remain the same, this operation is like bringing the 0’s from the left hand to the right hand. Figure 2 depicts this. This operation of moving 0’s to the right is called rotation.
与十进制数类似，乘以 10₂和 100₂时，分别在数字右边添加 1 个和 2 个 0。由于位数必须保持不变，这个操作类似于将左边的 0 移动到右边，如图 2 所示。这种将 0 向右移动的操作称为循环移位。

Rotation：(in binary number operations) Operation of moving one or more leftmost zeros in a binary number with a limited number of digits to the far right. This implies multiplying that number by 10b, 100b, etc.
 
循环：在二进制数运算中，将有限位数的二进制数中最左边的一个或多个 0 移动到最右边的操作，相当于将该数乘以 10₂、100₂等。

Rotation to the right is performed for multiplication, 1 bit for multiplication by 10b, 2 bits for multiplication by 100b, and so on. Note that here if multiplication is continued, then eventually overflow happens when the result becomes larger than a machine can handle (here because there are only 8 bits, not many numbers can be handled, but in a machine, with 128 bits the operation can go on much further).

向右循环移位用于乘法运算，乘以 10₂时移动 1 位，乘以 100₂时移动 2 位，依此类推。需要注意的是，如果继续进行乘法运算，当结果超出机器的表示范围时，最终会发生溢出（这里只有 8 位，能处理的数字有限，但在 128 位的机器中，运算可以进行得更远）

For multiplication by numbers like 3 (11b) and 6 (110b) and so forth, these numbers are broken into their components. For example:

对于乘以像 3（ $11_b$ ）和 6（ $110_b$ ）等数字的情况，这些数字可分解为其组成部分。例如：

$11_b=10_b+1$

Figure 2 Multiplication of a number by 10_b and 100_b.

${11}_b={10}_b+1$

Thus, multiplication of a binary number by $11_b$ includes multiplication of that number by $10_b$ , as above, and multiplication of the number by 1 (multiplication by 1 is trivial and does not change the number), and adding the results. Similarly, multiplication by $110_b$ includes multiplication by $100_b$ plus multiplication by $10_b$ :

因此，一个二进制数乘以 $11_b$ ，包括上述乘以 $10_b$ 的运算，以及乘以 1 的运算（乘以 1 结果不变），然后将结果相加。同样，乘以 $110_b$ 包括乘以 $100_b$ 加上乘以 $10_b$ ：

$110_b=100_b+10_b$

Both of these multiplications we have already seen. The results of the two multiplications then must be added together. Multiplication by all other numbers can be treated the same way.

这两种乘法运算我们前面已经讲过。然后必须将这两个乘法运算的结果相加。其他数字的乘法运算也可以用同样的方式处理。

Example 2

示例 2

Multiply the 10 - bit binary number $00,0110,0111_b$ by 7.

将 10 位二进制数 $00,0110,0111_b$ 乘以 7。

Solution

解答

Multiplication of the number by 7 consists of multiplication by $4+2+1$ . Because $7=111_b$ , then the number must be multiplied by $100_b$ , multiplied by $10_b$ , and multiplied by $1_b$ followed by adding all the results.

将这个数乘以 7，相当于分别乘以 $4+2+1$ 。因为 $7=111_b$ ，所以需要将这个数分别乘以 $100_b$ 、乘以 $10_b$ 和乘以 $1_b$ ，然后将所有结果相加。

$$\begin{array}{rl}& 00,0110,0111_b\times 100_b=01,1001,1100_b\\ & 00,0110,0111_b\times 10_b=00,1100,1110_b\\ & 00,0110,0111_b\times 1_b=00,0110,0111_b\end{array}$$

The final result is:

最终结果为：

$01,1001,1100_b+00,1100,1110_b+00,0110,0111_b=10,1101,0001_b$

You may want to check the results with decimal numbers. The initial number was 103, and the final answer is 721, which is $103\times 7$.

你可以用十进制数来验证结果。最初的数是 103，最终答案是 721，也就是 $103\times 7$ 。

In conjunction with multiplication is division. For division, numbers are shifted right. Shift right is shown in Figure 3. In dividing integer numbers, round - off errors can occur, as can be seen in the figure.

与乘法相关的是除法运算。在除法中，数字需要向右移位，如图 3 所示。在整数除法运算中，可能会出现舍入误差，如图中所示。

Shift right: (in binary number operations) Operation of moving all digits of a binary number (with a limited number of digits) to the right by one or more places. The left - most places are then filled with zeros. This implies dividing that number by $10_b$ , $100_b$ , etc. The rightmost digits are moved out and introduce the round-off error that occurs in the division.

右移：（在二进制数运算中）将有限位数的二进制数的所有位向右移动一位或多位，最左边的位置用 0 填充。这相当于将该数除以 $10_b$ 、 $100_b$ 等。最右边移出的位会导致除法中的舍入误差。

右移操作	二进制运算示例	说明
右移 1 位	$00111011/10_b=000111011$	此 0 被添加，此 1 移出并导致舍入误差
右移 2 位	$00111011/100_b=00001110$	这些 0 被添加，有舍入误差。若移出的是 0 则无舍入误差

Figure 3 Division in binary unsigned numbers Example

图 3：无符号二进制数的除法示例

---

1s and 2s complement

1 和 2 的补码

Note: The 1s complement and the 2s complement of a binary number are important because they permit the representation of negative numbers.
注意：二进制数的 1 的补码和 2 的补码很重要，因为它们允许表示负数。

∴ Finding the 1`s complement:-

∴ 找到 1 的补码：-

The 1`s complement of a binary number is found by changing all 1s to 0s and all 0s to 1s.
二进制数的 1 补码是通过将所有 1 更改为 0 并将所有 0 更改为 1 来找到的。

→ How to find 1`s complement of binary number.
→ 如何找到二进制数的 1 补码。

∴ 1`s complement using NOT gate.
∴ 1 的补码使用 NOT 门。

Q). Find the 1s complement of (10110)2 solution:- 1s complements = 01001

Finding the 2`s complement

求 2 的补码

The 2s complement of a binary number is found by adding 1 to the LSB of the 1s complement.
二进制数的 2 补码是通过将 1 的补码的 LSB 加到 1 的补码来找到的。

∴ 2s complement = (1s complement) + 1
∴ 2 的补码 = （1 的补码） + 1

→ How find 2`s complement of binary number?
→ 如何找到二进制数的 2 的补码？

∴ Alternative way to find direct 2`s complement
∴ 查找直接 2 补码的另一种方法

• Start at the right with the LSB and write the bits as they are up to and including the first 1.
  从右边的 LSB 开始，然后写入 bits，因为它们一直到 1 并包括前 1。
• Yake the 1`s complement of the remaining bits
  Yake 对剩余位的 1 的补码

In the above solution, we should write the same binary digits from right to left until we found 1, after that change the remaining bits into 1`s complement as shown above.
在上面的解决方案中，我们应该从右到左写相同的二进制数字，直到找到 1，然后将剩余的位更改为 1 的补码，如上所示。

→ Subtraction using 1`s complement

→ 使用 1 的补码进行减法

• Step 1:- Take 1`s complement of subtrahend
• 第 1 步：- 取 1 的 subtrahend 补码

• Step 2:- Add 1`s complement of subtrahend with minuend
• 第 2 步：- 将 1 的 subtrahend 补码与 minuend 相加

• Step 3:- If got a carry, add the carry to its LSB. Else take 1’s complement of the result and put negative sign
• 第 3 步：- 如果有 carry，将 carry 添加到其 LSB 中。否则取 1 的结果补码并加上负号

Subtracting using 2`s complement
使用 2 的补码进行减法

Step 1. Take 2`s complement of subtrahend
步骤 1.取 2 的 subtrahend 补码

Step 2. Add 2`s complement of subtrahend with minuend
步骤 2。将 subtrahend 的 2 补码与 minuend 相加

Step 3. If there is no carry , the result is negative and take the 2`s complement of above result and place negative sign in the final result.
步骤 3。如果没有 carry ，则结果为负数，取上述结果的 2 补码，并在最终结果中放置负号。

---

篇外 1：Why did ones’ complement decline in popularity?

1. 硬件实现复杂度

Two’s complement is generally simpler to implement in hardware than ones’ complement, except for one thing: if one wants a “live” readout of register values using one set of lights for positive numbers and one set for negative numbers (blanking whichever set isn’t appropriate) that can be accommodated very cheaply and easy with ones’-complement using one small transistor per bulb and a pair of large transistors to act as master enables for the positive and negative lights.

除了一种情况外，在硬件中实现补码（二进制补码）通常比反码（一的补码）更简单：如果想要使用一组灯显示正数、另一组灯显示负数来实时读出寄存器的值（熄灭不适用的那组灯），那么使用反码时，每个灯泡只需一个小晶体管，再用一对大晶体管作为正数和负数灯的主控使能，就能以低成本轻松实现。

If a system were to use two’s-complement, the values displayed for negative numbers would be off by one, and a significant amount of extra circuitry would be needed for each register’s readout to correct it.

如果一个系统使用补码，负数显示的值会差1，并且每个寄存器的读数都需要大量额外的电路来纠正这一问题。

2. 整数运算优势

Two’s-complement integer math is better in just about every other way, however.

然而，在几乎其他所有方面，补码的整数运算都更优。

3. 表示唯一性

zero only has one representation, with all-zero bits, which means testing for equality with zero is straightforward (which has knock-on effects on implementations of equality testing etc. since the latter can be implemented using subtraction, which also works for ordering values).

零只有一种表示形式，即所有位都为零，这意味着测试与零是否相等很简单（这对相等性测试等的实现有连锁反应，因为后者可以通过减法实现，减法也适用于对值进行排序）。

4. 运算一致性

addition, subtraction, and multiplication of two signed input values of length n can use the same implementation as the unsigned variants, modulo 2^{n};

两个长度为n的有符号输入值的加法、减法和乘法，可以使用与无符号变体相同的实现方式，对2的n次方取模；

With two’s complement, ADD and SUB are the same for both number types, except for overflow flags, so typically, a CPU sets both an unsigned overflow and a signed overflow flag for each ADD or SUB and this is easier than making 2 kinds of ADD and 2 kinds of SUB.

使用补码时，除了溢出标志外，两种数（有符号数和无符号数）的加法（ADD）和减法（SUB）操作是相同的。因此，通常情况下，CPU在每次加法或减法操作时都会同时设置无符号溢出标志和有符号溢出标志，这比设计两种加法和两种减法操作要容易。

With 2’s complement, the processor does not need to know whether it is dealing with a signed number or an unsigned number.

使用补码时，处理器不需要知道它处理的是有符号数还是无符号数。

5. 存在形式

Ones’ complement systems still exist, e.g. the UNIVAC 1100/2200 series, but as you mention they are rare (and existent probably only for historical reasons).

反码系统仍然存在，例如UNIVAC 1100/2200系列，但正如你所说，它们很罕见（可能只是由于历史原因才存在）。

6. 在现代计算中的应用

Not quite an answer but an observation. While ones’ complement machines are now almost extinct, ones’ complement computations are still here, and in large scales. Every IPv4 packet header has a checksum, that is calculated exactly as ones’ complement sum of 16bit words of the header contents.

这不算一个答案，只是一个观察。虽然反码机器现在几乎绝迹，但反码计算仍然大量存在。每个IPv4数据包头部都有一个校验和，它正是通过对头部内容的16位字进行反码求和来计算的。

Same with TCP and (optionally) UDP packets, where the whole packet is checksummed in the same way.

TCP和（可选的）UDP数据包也是如此，整个数据包都以相同的方式进行校验和计算。

7. 在浮点运算中的特点

Incidentally, ones’-complement would make sense with floating-point math if treats 0.1111111111111… with an unending string of ones as equivalent to 1.00000000.

顺便说一句，如果将无限个1的0.1111111111111…视为等同于1.00000000，那么反码在浮点运算中是有意义的。

Symmetry is more useful with floating point than with integer math, and thus ones’-complement would be advantageous there compared with two’s-complement. Sign magnitude also works (and is what many systems actually use) but ones’-complement could work essentially as well.

在浮点运算中，对称性比在整数运算中更有用，因此与补码相比，反码在这方面具有优势。符号幅度表示法也可行（而且许多系统实际上都在使用），但反码在本质上也能起到同样的作用。

8. 优缺点并存

While it is true that a ones’ complement implementation can save circuitry due the fact that a subtraction is just an addition with the subtrahend being negated (*1,2), it also adds complexity to (micro) program design and adds pitfalls (*3).

虽然反码实现确实可以节省电路，因为减法只是将减数取反后进行加法运算（注释1,2），但它也增加了（微）程序设计的复杂性，并带来了一些陷阱（注释3）。

Ones’ complement offers advantages in multi-word multiplication and division (*4), as well as for certain mathematical tasks (nearing zero from either side). But it adds complexity to hardware and/or software as every operation crossing zero needs an adjustment.

反码在多字乘法和除法（注释4）以及某些数学任务（从正负两个方向接近零）中具有优势。但它增加了硬件和/或软件的复杂性，因为每次跨越零的运算都需要进行调整。

*1 - That’s why the Pascaline uses nines’ complement
这就是 Pascaline 使用 9 补码的原因
 
*2 - But only if it’s not negative zero and so on.
但前提是它不是负零，依此类推。
 
*3 - Like the need to always know if a comparison is meant to be numeric and integer so a correction for +/- 0 is to be applied.
就像需要始终知道比较是否是数字和整数一样，因此要对 +/- 0 进行校正。
 
*4 - As no additional step for sign calculations is needed.
因为不需要额外的符号计算步骤。

---

篇外 2：Why is the apostrophe positioned differently in “ones’ complement” than “two’s complement”?

1. 关于“one’s complement”中撇号的位置解释

The phrase “one’s complement” is a reference to the operation of taking the complement of a single bit. When you have a single bit, say 0, its complement is 1, and vice versa. This is the fundamental operation from which the concept of one’s complement for multi - bit numbers is derived. The possessive apostrophe here indicates that it’s the complement of one (bit).

“one’s complement”这个短语指的是对单个比特进行取补的操作。当你有一个单独的比特，比如说0，它的补码是1，反之亦然。这是多位数字的反码（一的补码）概念所衍生的基本操作。这里的所有格撇号表明它是一个（比特）的补码。

2. 与“two’s complement”撇号位置差异的对比

In “two’s complement”, the “two” refers to the base of the number system (binary, base - 2). To find the two’s complement of a number, you first take the one’s complement and then add 1. The name “two’s complement” comes from the fact that you are essentially adding the number to $2^n$ (where $n$ is the number of bits) and then taking the result modulo $2^n$ . The apostrophe in “two’s” is also a possessive, indicating that it’s related to the number two (the base of the binary system).

在“two’s complement”中，“two”指的是数字系统的基数（二进制，基数为2）。要找到一个数的补码（二进制补码），你首先取其反码（一的补码），然后加1。“two’s complement”这个名称来自于这样一个事实，即你本质上是将该数字加上 $2^n$ （其中 $n$ 是比特数），然后对 $2^n$ 取模。“two’s”中的撇号也是所有格形式，表示它与数字二（二进制系统的基数）有关。

3. 关于撇号位置的另一种解释尝试

Another way to think about it could be that “one’s complement” is about the operation on each individual “one” (bit), while “two’s complement” is about an operation related to the number system based on two. It’s a bit of a stretch, but it might help in understanding the difference in the apostrophe placement.

另一种思考方式可能是，“one’s complement”是关于对每个单独的“一”（比特）进行的操作，而“two’s complement”是关于与基于二的数字系统相关的一种操作。这有点牵强，但它可能有助于理解撇号位置的差异。

4. 从语言习惯角度的说明

It’s just the way these terms have been established in the field of digital electronics and computer science. The language used to describe these concepts has evolved over time, and the current usage of apostrophes in “one’s complement” and “two’s complement” has become standard.

这只是这些术语在数字电子学和计算机科学领域中已经确立的方式。用于描述这些概念的语言随着时间的推移而演变，“one’s complement”和“two’s complement”中撇号的当前用法已经成为标准。

– houninym
Commented Dec 18, 2019 at 8:28

---

via:

• 1’s and 2’s complement of a Binary Number - GeeksforGeeks
  https://www.geeksforgeeks.org/1s-2s-complement-binary-number/

• Efficient method for 2’s complement of a binary string - GeeksforGeeks
  https://www.geeksforgeeks.org/efficient-method-2s-complement-binary-string/

• Difference Between 1’s Complement Representation and 2’s Complement Representation Technique - GeeksforGeeks
  https://www.geeksforgeeks.org/difference-between-1s-complement-representation-and-2s-complement-representation-technique/

• Signed Binary Numbers and Two’s Complement Numbers
  https://www.electronics-tutorials.ws/binary/signed-binary-numbers.html

• One’s and Two’s Complement of Binary Number | Electrical Academia
  https://electricalacademia.com/digital-circuits/ones-twos-complement/

• 1s And 2s Complement | BimStudies.Com
  https://bimstudies.com/docs/digital-logic/binary-systems/1s-2s-complement/

• Why did ones’ complement decline in popularity?
  https://retrocomputing.stackexchange.com/questions/7095/why-did-ones-complement-decline-in-popularity

• Why is the apostrophe positioned differently in “ones’ complement” than “two’s complement”?
  https://english.stackexchange.com/questions/520897/why-is-the-apostrophe-positioned-differently-in-ones-complement-than-twos-c

• 原码，反码(ones’ complement)，补码(two’s complement) - 简书
  https://www.jianshu.com/p/4da81d3afabb