在现实应用中,许多学习方法都涉及距离计算,而高维空间会给距离计算带来很大的麻烦。例如当维数很高时,甚至连计算内积都很不容易。
这实际上,是所有机器学习都面临的严重障碍,这被称为“维数灾难(即样本非常洗漱,距离计算很困难)”。
而缓解维数灾难的两个普遍做法是降维和特征选择。
降维指的是:通过某种数学变换将原始高维属性空间转变为一个低维子空间,在这个低维的子空间中,样本密度大幅度提高,距离计算也变得很容易。
我们通常要求高维空间(原始空间)中样本之间的距离在低维空间中得以保持。
根据这个要求,我们会很自然的想到使用欧氏距离,因为欧氏距离有一个非常好的特性就是,它能够在变换中,保持相对距离不变。
所以,现在我们介绍一种非常经典的降维方法,即多维缩放(MDS)。从缩放(scale)这个词语我们就能够看出,这个方法会保持它的相对距离不变。
MDS算法的思想其实是巧妙的,即通过利用对点(数据)做平移,旋转,翻转等操作,点的距离是不变的这一特性来对原始数据进行操作。
现在我们假设原始的距离矩阵为D,而B为降维后样本的内积矩阵,Z为最后输出的降维矩阵。
先令:B=Z*ZT(Z乘以Z的转置),那么
B=Z*ZT
=(Z*M)(Z*M)T(M是一组正交基)
=Z*M*MT*Z
=Z*ZT
所以,我们可以看到。我们通过对M这一正交基,对Z做正交变换,并不会影响B的值。而实际上,正交变换刚好就是对数据做旋转、翻转的。
所以,假如我们想通过B反算出Z,那得到的肯定不是真正的Z,我们得到的只是一种Z的一种任意一种正交变换。然而,这并不影响我们使用,因为我们想要的只是相对的东西。
所以,我们的流程是,先算D,然后通过D来算出B,然后再由B来算出Z。
而D是好算的,其中每个元素值为:

算好D之后,我们要想办法从D算出B。
我们令降维后的矩阵Z被中心化,中心化你可以把他理解成一种平移。它实际做的是将每个样本向量减去整个样本集的均值向量。然后呢,所有样本向量求和之后就等到一个零向量。(5,7的均值为6,中心化后为-1,1。求和之后为0)。
而B=Z*ZT,所以,矩阵B的每一列以及每一行求和之后都等于0。
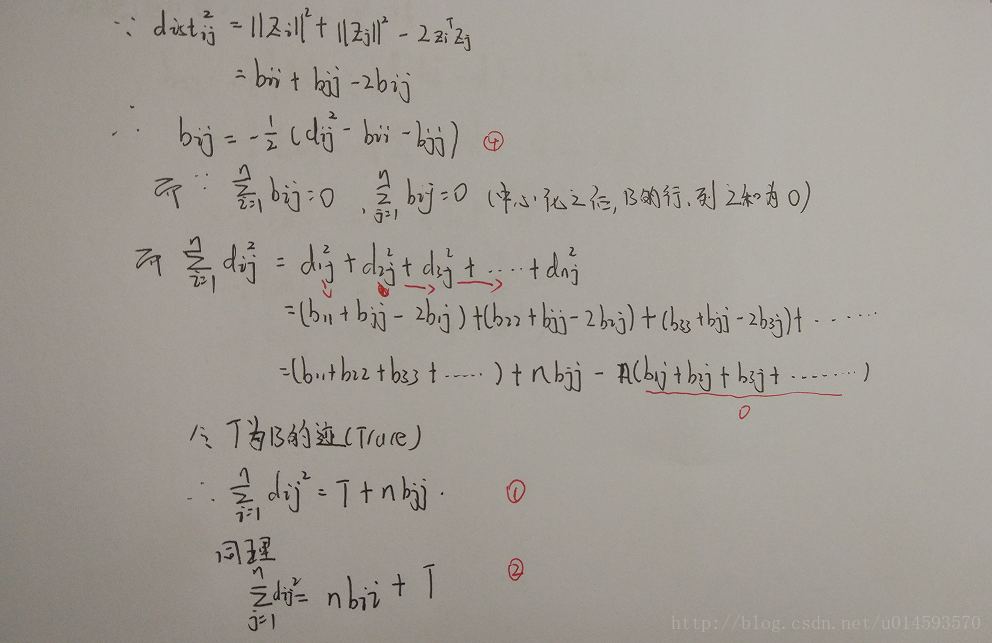

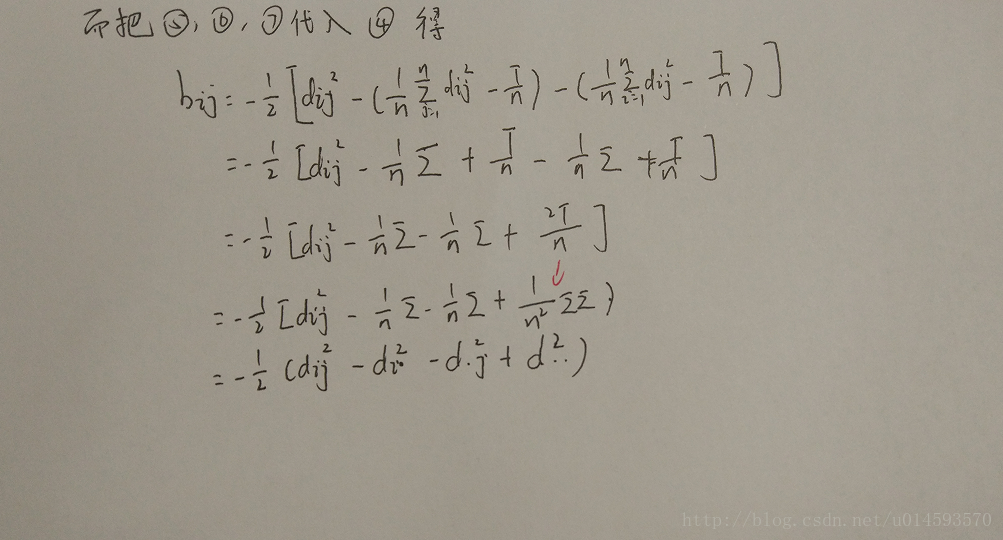
OK,至此,我们就可以通过矩阵D来得到矩阵B了。下一步我们要通过B来求Z。
而因为B实际上是一个对称矩阵,所以我们对它做特征值分解,给出它的特征值和特征向量。接下来就如西瓜书上写的那样。

至此,MDS算法讲解完毕。
参考文章、
机器学习-周志华
维度打击,机器学习中的降维算法:ISOMAP & MDS
迹的几何意义是什么






















 2410
2410

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








