核密度估计 Kernel Density Estimation(KDE)

写在前面

给定一个样本集，怎么得到该样本集的分布密度函数，解决这一问题有两个方法：

1.参数估计方法
简单来讲，即假定样本集符合某一概率分布，然后根据样本集拟合该分布中的参数，例如：似然估计，混合高斯等，由于参数估计方法中需要加入主观的先验知识，往往很难拟合出与真实分布的模型；
2.非参数估计
和参数估计不同，非参数估计并不加入任何先验知识，而是根据数据本身的特点、性质来拟合分布，这样能比参数估计方法得出更好的模型。核密度估计就是非参数估计中的一种，由Rosenblatt (1955)和Emanuel Parzen(1962)提出，又名Parzen窗（Parzen window）。Ruppert和Cline基于数据集密度函数聚类算法提出修订的核密度估计方法。

直方图到核密度估计

给定一个数据集，需要观察这些样本的分布情况，往往我们会采用直方图的方法来进行直观的展现。该方法简单，容易计算，但绘制直方图时，需要确定bins，如果bins不同，那么最后的直方图会产生很大的差别。如下面的两直方图，右边比左边的直方图多划分了bins，导致最后的结果有很大的差别，左边时双峰的，右边时单峰的。

除此之外，直方图还存在一个问题，那就是直方图展示的分布曲线并不平滑，即在一个bin中的样本具有相等的概率密度，显然，这一点往往并不适合。解决这一问题的办法时增加bins的数量，当bins增到到样本的最大值时，就能对样本的每一点都会有一个属于自己的概率，但同时会带来其他问题，样本中没出现的值的概率为0，概率密度函数不连续，这同样存在很大的问题。如果我们将这些不连续的区间连续起来，那么这很大程度上便能符合我们的要求，其中一个思想就是对于样本中的某一点的概率密度，如果能把邻域的信息利用起来，那么最后的概率密度就会很大程度上改善不连续的问题，为了方便观察，我们看另外一副图。

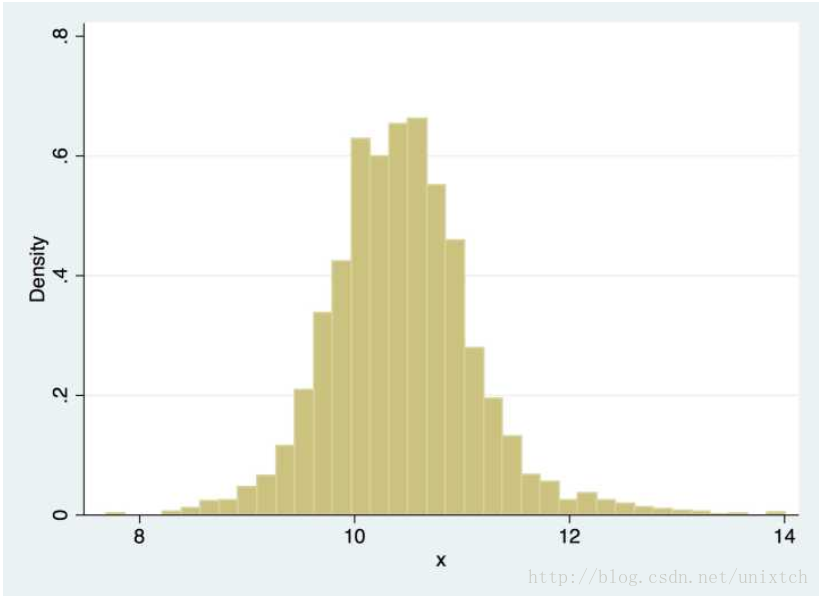
现在我们假设要求x处的密度函数值，根据上面的思想，如果取x的邻域[x-h,x+h]，当h->0的时候，我们便能把该邻域的密度函数值当作x点的密度函数值。用数学语言写就是：

$$\hat f(x)={1 \over 2h}\lim_{h->0}{N_{xi \in [x-h,x+h]} \over N_{total}}$$ $N_{xi \in [x-h,x+h]}$时该邻域中的样本点数量， $N_{total}$样本集的总数量，最后对该邻域内的密度值取平均便得到 $x$点的密度函数值$f(x)$。把上面的式子进行改写： $$\hat f(x)={1 \over 2hN_{total}} \sum_{i=x-h}^{x+h}x_i={1 \over hN_{total}}\sum_{i}{{|x-x_i|} \over 2h}<1,h->0$$ 这里h如果选的太大，肯定不符合h趋向于0的要求。h选的太小，那么用于估计f(x)的点实际上非常少。这也就是非参数估计里面的bias-variance tradeoff，也就是偏差和方差的平衡。这样后还是存在一个问题，那就是概率密度函数依然不够平滑（因为两个数之间的存在无数个数啊）。

记 $K(x)={1 \over 2}1\{x<1\}$，那么： $$\hat f(x)={1 \over hN_{total}}\sum_{i}K({{|x-x_i|} \over h})$$ 由于需要满足概率密度的积分为1，所以： $$\int \hat f(x)={1 \over hN_{total}}\sum_{i}\int K({{|x-x_i|} \over h}dx={1 \over N_{total}}\sum_{i}\int K(t)dt=\int K(t)dt$$ 也就是要满足 $K(t)$的积分等于1也就满足了 $\hat f(x)$的积分为1。如果把 $K(t)$当作其他已知的概率密度函数，那么问题就解决了，最后的密度函数也就连续了。

核函数

从支持向量机、meansift都接触过核函数，应该说核函数是一种理论概念，但每种核函数的功能都是不一样的，这里的核函数有uniform,triangular, biweight, triweight, Epanechnikov,normal等。这些核函数的图像大致如下图：

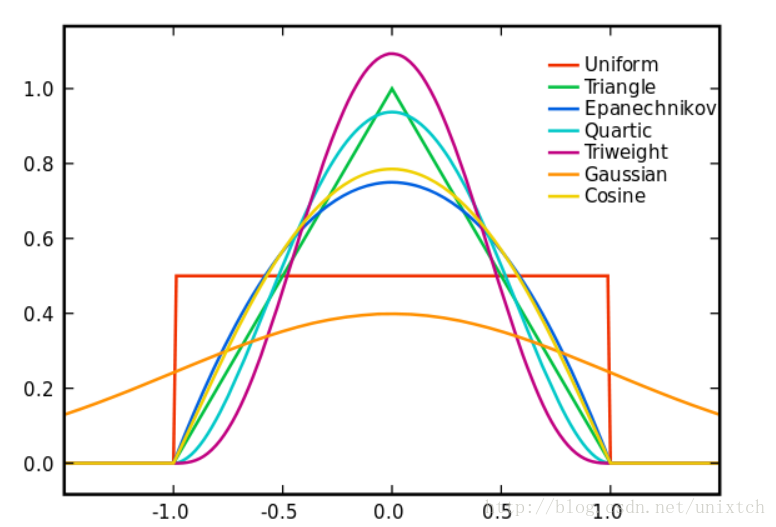
有言论称Epanechnikov 内核在均方误差意义下是最优的，效率损失也很小。这一点我没有深究是如何得到的，暂且相信吧^^。由于高斯内核方便的数学性质，也经常使用 K(x)= ϕ(x)，ϕ(x)为标准正态概率密度函数。
从上面讲述的得到的是样本中某一点的概率密度函数，那么整个样本集应该是怎么拟合的呢？将设有N个样本点，对这N个点进行上面的拟合过后，将这N个概率密度函数进行叠加便得到了整个样本集的概率密度函数。例如利用高斯核对$X=\{x_1 = −2.1, x_2 = −1.3, x_3 = −0.4, x_4 = 1.9, x_5 = 5.1, x_6 = 6.2\}$ 六个点的“拟合”结果如下：


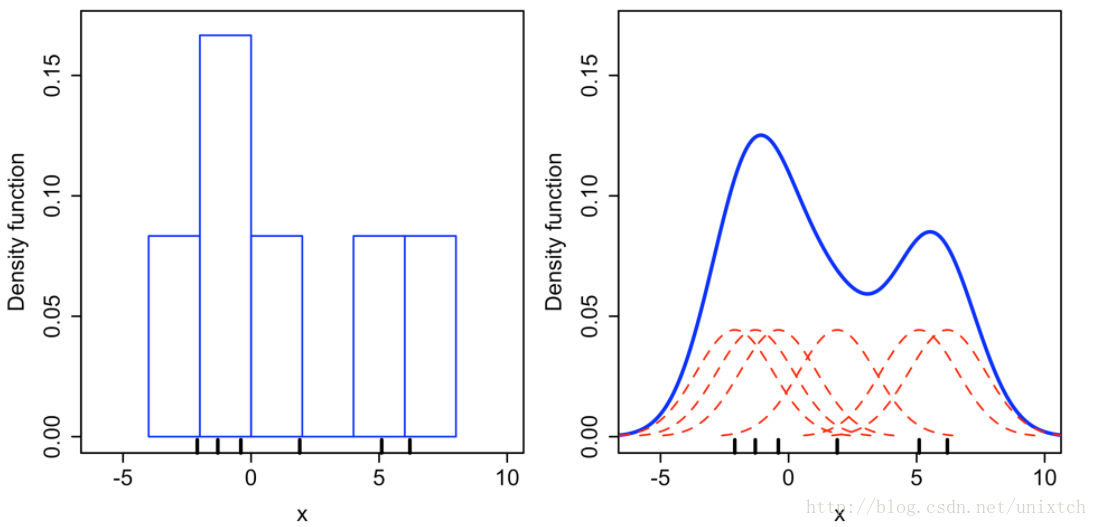
左边是直方图，bin的大小为2，右边是核密度估计的结果。

带宽的选择

在核函数确定之后，比如上面选择的高斯核，那么高斯核的方差，也就是h（也叫带宽，也叫窗口，我们这里说的邻域）应该选择多大呢？不同的带宽会导致最后的拟合结果差别很大。同时上面也提到过，理论上h->0的，但h太小，邻域中参与拟合的点就会过少。那么借助机器学习的理论，我们当然可以使用交叉验证选择最好的h。另外，也有一个理论的推导给你选择h提供一些信息。
在样本集给定的情况下，我们只能对样本点的概率密度进行计算，那拟合过后的概率密度应该核计算的值更加接近才好，基于这一点，我们定义一个误差函数，然后最小化该误差函数便能为h的选择提供一个大致的方向。选择均平方积分误差函数(mean intergrated squared error)，该函数的定义是：

$$MISE(h)=E\int{(\hat f(x)-f(x))}^2dx$$ 在weak assumptions下， $MISE (h) =AMISE(h) + o(1/(nh) + h4)$ ，其中AMISE为渐进的MISE(这里我没搞懂是怎么推导出来的)。而AMISE有： $$AMISE(h)={R(K) \over nh}+{1 \over 4}m_2(K)^2h^4R(f^{''})$$ 其中： $$R(K)=\int K(x)^2dx,\quad m_2(K)=\int x^2K(x)dx$$ 最小化MISE(h)等价于最小化AMISE(h)，求导，令导数为0有： $${ \partial \over \partial h } AMISE(h)= -{R(k) \over nh^2}+m_2(K)^2h^3R(f^{''})=0$$ 得： $$h_{AMISE}={{R(K)}^{1 \over 5} \over m_2(K)^{2 \over 5}R(f^{''})^{1 \over 5}n^{1 \over 5}}$$ 当核函数确定之后，h公式里的R、m、f”都可以确定下来，h便存在解析解。如果带宽不是固定的，其变化取决于估计的位置（balloon estimator）或样本点（逐点估计pointwise estimator），由此可以产产生一个非常强大的方法称为自适应或可变带宽核密度估计。

总结

核密度估计完全利用数据本身信息，避免人为主观带入得先验知识，从而能够对样本数据进行最大程度得近似（相对于参数估计）。而多样得核函数也为实际应用中提供了选择，但在带宽的选择上存在一些问题，当然可以根据上面的推导为带宽的选择提供一些方向。至于实现方面，sklearn核scipy都对核密度估计进行了实现核优化，这应该是个不错的选择。

参考

https://www.zhihu.com/question/27301358/answer/105267357?from=profile_answer_card
http://blog.csdn.net/yuanxing14/article/details/41948485