MLA实现及其推理上的十倍提速——逐行解读DeepSeek V2中多头潜在注意力MLA的源码(图、公式、代码逐一对应)

前言

想来也是巧，最近deepseek实在是太火了，就连BAT这类大厂全部宣布接入deepseek，更不用说一系列国企、车企等各行各业的传统行业、企业都纷纷接入deepseek

与此同时，也有很多公司、开发者对本地部署deepseek的诉求居高不下，我们也服务了一些B端客户，此文《一文速览DeepSeek-R1的本地部署——可联网、可实现本地知识库问答：包括671B满血版和各个蒸馏版的部署》也提供了一些本地部署的方法，然

1. 2.16日上午，我司deepseek项目实战营一学员提问：“清华出的单卡4090部署满血deepseek能实现吗”
2. 2.16日下午，我个人在中南组织了长沙第一届大模型与具身研讨会(参会者包括我司在内的各公司的大模型工程师、以及长沙三大985的博士生、硕士生)
   期间聊到了R1的本地部署
   2.16日晚上，则与国防科大的一博士生朋友聊到了KTransformer——在24G显存的单卡4090上部署deepseek R1 671B Q4量化版
   
   实在是因为R1本地部署太火了，故
   2.17日中午
   一方面，我让同事基于KTransformer，尝试下单卡4090部署R1 Q4量化版
   二方面，我则同步研究KTransformers的背后原理了

结果，在网上看KTransformers资料的时候，无意中看到一篇帖子《DeepSeek-V2 高性能推理 (1)：通过矩阵吸收十倍提速 MLA 算子》——部分内容引用在本文的第二部分，让我再次关注到了DeepSeek-V2对MLA的实现

换言之，虽然此文《MTP——我对DeepSeek V3中多token预测MTP的代码实现(含对V3官方MoE、MLA推理代码的解读)》开头说

对于V3、R1都没有开源他们最核心的训练数据、训练代码
比如V3只是开源了模型权重、模型结构和推理脚本——比如本文前两个部分重点分析的作为推理时实例化模型用的model.py，它的整个文件 中的代码，都只是推理代码

但好歹V3沿用的MoE架构、MLA算法，在对应的前置模型DeepSeekMoE、deepseek V2中实现且把代码对外开源了

本文，便来解读下DeepSeek V2对MLA算法的实现

• 本文的出发点虽然是源码解析「而关于MLA算法的详尽细致的解析，请参见此文《一文通透DeepSeek V2——通俗理解多头潜在注意力MLA：改进MHA，从而压缩KV缓存，提高推理速度》」
  
  但过程中 我会极其注重：图片 公式 代码的一一对应，包括每个矩阵的维度变化全部具体数字体现，且有时同一个公式符号及其在V2中设置的数字 我会用同一个颜色的字体
  一方面，那样会很通透
  二方面，当你真正完全理解一个算法之后，你是可以脱离原稿，手推公式、手绘其图的，而有了公式、流程图的情况下，代码便可快速写出
  如此，我希望帮更广大的读者降低门槛、提高效率，并从技术状态带入到更深入的科研状态——我也是这么经历的
• 且本文的「第二部分 MLA推理层面的改进：通过矩阵吸收十倍提速 MLA算子」围绕V2论文中一嘴带过的
  “Fortunately, due to the associativelaw of matrix multiplication, we can absorb 𝑊𝑈𝐾into 𝑊𝑈𝑄, and 𝑊𝑈𝑉into 𝑊𝑂.”
  
  最终花了大量的篇幅，和本文的第一部分一样，依然通过一系列围绕「图、公式、代码」的三者对比，不厌其烦、足够耐心的说清楚该问题
• 至于DeepSeekMoE对MoE架构的实现「本部分分析的代码来自：deepseek-moe-16b-chat/blob/main/modeling_deepseek.py 」，则后续把该部分移动到了此文《一文速览DeepSeekMoE：从Mixtral 8x7B到DeepSeekMoE(含MoE架构的实现及DS LLM的简介)》中的第4部分

第一部分 DeepSeek V2对MLA算法的实现

注，本部分分析的是deepseek-ai/DeepSeek-V2-Chat/tree/main中的DeepSeek-V2/blob/main/modeling_deepseek.py，这个1907行的modeling_deepseek.py先后实现了如下功能

1. 首先是一个用于处理4D因果注意力掩码的函数 `_prepare_4d_causal_attention_mask`，它被包装成一个FX图中的叶子函数，这意味着该函数不会被追踪，只会作为图中的一个节点出现。接下来是一个日志记录器 `logger` 和一个配置常量 `_CONFIG_FOR_DOC`
2. 然后定义了一个函数 `_get_unpad_data`，该函数从注意力掩码中提取非填充数据。它计算每个批次中的序列长度，找到非零元素的索引，并计算累积序列长度
3. 接下来是 `DeepseekV2RMSNorm` 类的定义，这是一个等效于 T5LayerNorm 的归一化层。它在前向传播过程中计算输入的方差，并使用方差和一个小的常数来归一化输入
4. `DeepseekV2RotaryEmbedding` 类实现了旋转位置嵌入。它在初始化时计算逆频率，并在前向传播过程中根据输入的序列长度设置余弦和正弦缓存
   
   以下的三个类，则从不同的角度对DeepseekV2RotaryEmbedding类 进行了各自的扩展
     `DeepseekV2LinearScalingRotaryEmbedding` 类扩展了 `DeepseekV2RotaryEmbedding`，添加了线性缩放功能。它在 `_set_cos_sin_cache` 方法中对时间步进行缩
     `DeepseekV2DynamicNTKScalingRotaryEmbedding` 类进一步扩展了 `DeepseekV2RotaryEmbedding`，添加了动态 NTK 缩放功能。它根据序列长度动态调整基数和逆频率
     `DeepseekV2YarnRotaryEmbedding` 类是 `DeepseekV2RotaryEmbedding` 的另一个扩展，添加了基于 Yarn 的缩放功能。它使用了一些辅助函数来计算频率掩码和缩放因子
   
   至于`rotate_half` 函数用于旋转输入张量的一半隐藏维度，而 `apply_rotary_pos_emb` 函数则将旋转位置嵌入应用于查询和键张量
5. `DeepseekV2MLP` 类实现了一个多层感知机（MLP），它包含了门控投影、上投影和下投影层，并在前向传播过程中应用激活函数
   `MoEGate` 类实现了一个混合专家门控机制。它计算门控得分，选择前 k 个专家，并在训练过程中计算辅助损失
   `DeepseekV2MoE` 类是一个包含共享专家的混合专家模块。它在前向传播过程中根据门控得分选择专家，并在推理过程中对输入进行排序和分配
6. `DeepseekV2Attention` 类实现了多头注意力机制。它在前向传播过程中计算查询、键和值，并应用旋转位置嵌入
   `DeepseekV2FlashAttention2` 类继承自 `DeepseekV2Attention`，实现了闪存注意力机制。它在前向传播过程中处理填充标记，并调用闪存注意力的公共 API
7. `DeepseekV2DecoderLayer` 类实现了一个解码器层，包含自注意力和 MLP 模块，并在前向传播过程中应用层归一化
   `DeepseekV2Model` 类实现了一个包含多个解码器层的 Transformer 解码器。它在前向传播过程中嵌入输入标记，并通过解码器层计算隐藏状态
8. 最后，`DeepseekV2ForCausalLM` 和 `DeepseekV2ForSequenceClassification` 类分别实现了用于因果语言建模和序列分类的模型。它们在前向传播过程中计算损失和预测结果

1.1 DeepseekV2RMSNorm

1.2 DeepseekV2RotaryEmbedding

1.3 对MoE架构的实现与改进

1.4 DeepseekV2Attention的中的初始化：__init__、_init_rope、_shape

这段代码定义了一个名为 `DeepseekV2Attention` 的类，它基于多头注意力MHA实现了多头潜在注意力MLA

1. 在类的构造函数 `__init__` 中，首先初始化了一些配置参数，如隐藏层大小、注意力头的数量、最大位置嵌入等。如果没有提供层索引 `layer_idx`，会发出警告。然后，初始化了一些线性投影层和归一化层，用于处理查询、键和值的投影
2. `_init_rope` 方法用于初始化旋转位置嵌入（RoPE）。根据配置中的 `rope_scaling` 参数，它可以选择不同的旋转位置嵌入实现，如线性缩放、动态 NTK 缩放和 Yarn 缩放
3. `_shape` 方法用于调整张量的形状，使其适应多头注意力机制的计算需求。
4. 在 `forward` 方法中，该类实现了多头注意力机制的前向传播过程
   首先计算查询、键和值的投影，并应用旋转位置嵌入
   然后，计算查询和键之间的注意力权重，并应用注意力掩码
   接着，对注意力权重进行归一化和丢弃，最后计算注意力输出
5. 如果提供了 `past_key_value`，该方法还会更新键和值的缓存，以支持自回归解码
   最终，方法返回注意力输出、注意力权重和更新后的键值缓存

总的来说，这段代码实现了一个复杂的多头注意力机制，支持多种旋转位置嵌入的缩放方法，并且能够处理自回归解码的缓存更新

1.5 DeepseekV2Attention中的forward实现：MLA核心算法

1.5.1 forward的参数与相关设置

forward接收多个输入参数，包括

• 隐藏状态 `hidden_states`，对应公式中的 ，是一个大小为 [batch_Size, sequence_length, hidden_size] 的矩阵，其中 hidden_size 具体为 5120
• 可选的注意力掩码 `attention_mask`
• 位置 ID `position_ids`
• 过去的键值对缓存 `past_key_value`
• 是否输出注意力权重 `output_attentions`
• 是否使用缓存 `use_cache`

def forward(
        self,
        hidden_states: torch.Tensor,                      # 输入的隐藏状态张量
        attention_mask: Optional[torch.Tensor] = None,    # 可选的注意力掩码张量
        position_ids: Optional[torch.LongTensor] = None,  # 可选的位置ID张量
        past_key_value: Optional[Cache] = None,           # 可选的过去键值缓存
        output_attentions: bool = False,                  # 是否输出注意力权重
        use_cache: bool = False,                          # 是否使用缓存
        **kwargs,  
    ) -> Tuple[torch.Tensor, Optional[torch.Tensor], Optional[Tuple[torch.Tensor]]]:                           # 返回值类型

首先，方法检查是否在 `kwargs` 中传递了 `padding_mask`，并发出警告，提示将来版本中将移除该参数

       # 如果在kwargs中传递了padding_mask
       if "padding_mask" in kwargs:  
            # 发出警告，提示使用attention_mask代替padding_mask
            warnings.warn(
                "Passing `padding_mask` is deprecated and will be removed in v4.37. Please make sure use `attention_mask` instead.`"  

然后，它获取批次大小 `bsz` 和查询长度 `q_len`

        bsz, q_len, _ = hidden_states.size()      # 获取批次大小和查询长度

1.5.2 对Q向量的降维、拆分且升维、合并

接下来，如下图所示，从下往上看，首先是一个input hidden ——对应于代码中的hidden_states向量，该输入相当于[batch_Size, sequence_length, hidden_size] 的矩阵，其中 hidden_size 具体大小为 5120，即

如上图左侧所示，MLA 中对 Q 投影矩阵也做了一个低秩分解，先后涉及 降维矩阵q_a_proj 和 升维矩阵q_b_proj

        # 对隐藏状态进行线性投影和归一化，生成查询张量
        q = self.q_b_proj(self.q_a_layernorm(self.q_a_proj(hidden_states)))  

        # 调整查询张量的形状
        q = q.view(bsz, q_len, self.num_heads, self.q_head_dim).transpose(1, 2)  

首先降Q

方法会先对隐藏状态进行线性投影和归一化，生成潜在查询张量 `q`——

其中，生成潜在查询向量的这个过程属于降维

• 
  此时的维度为
  可以很清楚的看到从到，确实降维了
• 而q_a_proj 对应的就是降维矩阵——据此文的「2.2.1 MLA对Q K V的压缩：先对KV联合压缩后升维，再对Q压缩后升维」节，可知
  其大小为 [hidden_size, q_lora_rank] = [5120, 1536]

其次是拆分、且升维

在拆分角度上，如下图所示，将查询向量拆分为两个部分

• 不包含位置嵌入的部分 `q_nope`——
   
  此时对应的维度为，其中H = 128，属于head数
• 包含位置嵌入的部分 `q_pe`——
   
  此时对应的维度，其中H = 128，属于head数

对应的代码则如下所示

        q_nope, q_pe = torch.split(
            # 将查询张量拆分为不包含位置嵌入的部分和包含位置嵌入的部分
            q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1  
        )

提前提一嘴，将以上这两部分拼接便可得到最终的Q向量

在维度角度上，降维之后，后续会做升维，而q_b_proj 对应的就是

1. 升维矩阵——据此文的「2.2.1 MLA对Q K V的压缩：先对KV联合压缩后升维，再对Q压缩后升维」节，可知 
2. 旋转矩阵——据此文的「2.2.1 MLA对Q K V的压缩：先对KV联合压缩后升维，再对Q压缩后升维」节，可知

合并之后的大矩阵

故q_b_proj 的大小为
[q_lora_rank,         num_heads *       q_head_dim]
= [q_lora_rank,      num_attention_heads * (qk_nope_head_dim + qk_rope_head_dim)]
= [1536,                 128     *  (    128    +    64)]
= [1536,                 24576   ]

可以看到，q_head_dim = qk_nope_head_dim + qk_rope_head_dim

顺带提一下，上面这几个维度的设置 在此文《一文通透DeepSeek V2——通俗理解多头潜在注意力MLA：改进MHA，从而压缩KV缓存，提高推理速度》的「3.1.1 模型超参数」节中提到过

---

对于模型超参数，将Transformer层数设置为60，隐藏维度设置为5120，即——对应上面提到的 hidden_size 具体大小为 5120

在MLA中

• 将注意力头的数量设置为128——对应上面提到的num_attention_heads
• 每头维度设置为128——对应上面提到的qk_nope_head_dim
• KV压缩维度设置为512「可以看出」——这个维度就是下文马上要提到的512维的kv_lora_rank，其实也远远小于
  查询压缩维度设置为1536「对应上面提到的q_lora_rank，其为1536」——依然远小于
  
  对于解耦查询和键，设置每头维度为64——对应上面提到的qk_rope_head_dim，为64

  

1.5.3 对KV张量的降维、分裂K、拆分KV且升维

首先，需要对KV做压缩、降维

方法即对隐藏状态进行线性投影，生成压缩的键值对张量 `compressed_kv`

        # 对隐藏状态进行线性投影，生成压缩的键值对张量
        compressed_kv = self.kv_a_proj_with_mqa(hidden_states)  

第一，在维度角度上，属降维，故才有kv_a_proj_with_mqa 覆盖以下两个维度的矩阵

1. 512维的kv_lora_rank降维矩阵
   据此文的「2.2.1 MLA对Q K V的压缩：先对KV联合压缩后升维，再对Q压缩后升维」节，可知
2. 64维的qk_rope_head_dim旋转矩阵
   据此文的「2.2.1 MLA对Q K V的压缩：先对KV联合压缩后升维，再对Q压缩后升维」节，可知

即kv_a_proj_with_mqa 的大小为
[hidden_size， kv_lora_rank + qk_rope_head_dim]
= [5120, 512 + 64]
= [5120, 576]

本质上来讲，kv_a_proj_with_mqa的维度，相比input hidden 的维度大小5120 还是很低的

第二，分裂K，即对于其中的K向量而言

1. 一部分K：和V一块做联合压缩
2. 一部分K：做RoPE编码

从而演变成两个部分

1. 不包含位置嵌入的部分compressed_kv——
2. 包含位置嵌入的部分 `k_pe`——
   

对应的代码为

        compressed_kv, k_pe = torch.split(
            # 将压缩的键值对张量拆分为不包含位置嵌入的部分和包含位置嵌入的部分
            compressed_kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1  
        )

其次，在潜在压缩空间中完成对KV cache的计算之后，K V拆分且各自升维

一方面，对于不包含位置嵌入的部分，方法继续对压缩的键值对张量进行线性投影和归一化

         # 调整键张量的形状
        k_pe = k_pe.view(bsz, q_len, 1, self.qk_rope_head_dim).transpose(1, 2) 

        # 对压缩的键值对张量进行线性投影和归一化
        kv = (
            self.kv_b_proj(self.kv_a_layernorm(compressed_kv))
            .view(bsz, q_len, self.num_heads, self.qk_nope_head_dim + self.v_head_dim)  # 调整键值对张量的形状
            .transpose(1, 2)  # 转置张量
        )

然后将键和值张量 `kv`，拆分为两个部分

1. 不包含位置嵌入的部分 `k_nope`——
   
2. 和值张量 `value_states`——
   

对应的代码则为

        k_nope, value_states = torch.split(
            # 将键值对张量拆分为不包含位置嵌入的部分和值张量
            kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1  
        )

二方面，在维度上，是升维的，故才有kv_b_proj 的大小为
[kv_lora_rank， num_heads * (q_head_dim - qk_rope_head_dim + v_head_dim)]
= [512, 128*( (128+64)-64 + 128 )]
= [512, 32768]
128、128分别对应分别对应k的升维矩阵  ——据此文的2.2.1节，可知，和v的升维 

其中，由于  只涉及 non rope 的部分，所以维度中把 qk_rope_head_dim——旋转矩阵 去掉了

且从上面的表述，可以看出来

1. q_head_dim的维度与上面的描述是一致的
   q_head_dim = qk_nope_head_dim + qk_rope_head_dim
2. kv_lora_rank/512 是 qk_nope_head_dim/128 的 4 倍且 K 和 V 共享 latent state
   qk_rope_head_dim/64 只有 qk_nope_head_dim/128 的一半

这两个比例关系结合起来 4+1/2=9/2，正是下图中 MLA KVCache per Token 大小的来源

且，即如此文《一文通透DeepSeek V2——通俗理解多头潜在注意力MLA：改进MHA，从而压缩KV缓存，提高推理速度》2.2节最后所说的
最终，单个Token产生的缓存包含了两个部分，即
其中，如上文说过的的有
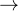
  个头，每个头——比如和向量的头维度为， 表示为transformer的层数表示为GQA中的组数
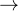
  、分别表示MLA中的KV压缩维度、解耦查询和键的the per-head dimension

在DeepSeek-V2中
被设置为——比如可以分别为512 128
被设置为——比如可以分别为64 128

最后，如果提供了 `past_key_value`，方法会更新键和值的缓存，并计算可用的序列长度 `kv_seq_len`

        kv_seq_len = value_states.shape[-2]     # 获取值张量的序列长度
        if past_key_value is not None:          # 如果提供了过去键值缓存
            if self.layer_idx is None:          # 如果没有提供层索引
                raise ValueError(
                    f"The cache structure has changed since version v4.36. If you are using {self.__class__.__name__} "  # 抛出错误，提示需要提供层索引
                    "for auto-regressive decoding with k/v caching, please make sure to initialize the attention class "
                    "with a layer index."
                )

            kv_seq_len += past_key_value.get_usable_length(kv_seq_len, self.layer_idx)  # 更新序列长度

1.6 MLA收尾：给q_pe, k_pe给加上rope且合并，然后做标准注意力计算

1.6.1 对查询向量、键向量的旋转位置编码且合并

在生成 QKV 向量之后后续的流程就基本上等同于标准的 MHA 计算了，唯一的区别在于只有 q_pe, k_pe 这两个部分给加上了 rope

比如，首先，计算attention score

然后对V做加权求和，得到attention输出

最后，经过矩阵投影，得到MLA的最终输出

具体而言，方法首先应用旋转位置嵌入

1. 将查询和键张量 `q_pe` 和 `k_pe` 进行旋转

           # 计算旋转位置嵌入的余弦和正弦值
           cos, sin = self.rotary_emb(value_states, seq_len=kv_seq_len)  
   
           # 应用旋转位置嵌入
           q_pe, k_pe = apply_rotary_pos_emb(q_pe, k_pe, cos, sin, position_ids)  

2. 接着，方法创建新的查询状态张量 `query_states` ，然后将旋转后的部分和不包含位置嵌入的部分合并便可得到最终的Q向量
   

   

   对应的代码如下

           # 创建新的查询状态张量
           query_states = k_pe.new_empty(bsz, self.num_heads, q_len, self.q_head_dim)
   
           # 将不包含位置嵌入的部分赋值给查询状态张量
           query_states[:, :, :, : self.qk_nope_head_dim] = q_nope
   
           # 将包含位置嵌入的部分赋值给查询状态张量
           query_states[:, :, :, self.qk_nope_head_dim :] = q_pe  
     

3. 创建新的键状态张量 `key_states`，并将旋转后的部分和不包含位置嵌入的部分合并，可得
   
   对应的示意图如下

   

   对应的代码如下

           # 创建新的键状态张量
           key_states = k_pe.new_empty(bsz, self.num_heads, q_len, self.q_head_dim) 
   
           # 将不包含位置嵌入的部分赋值给键状态张量 
           key_states[:, :, :, : self.qk_nope_head_dim] = k_nope  
   
           # 将包含位置嵌入的部分赋值给键状态张量
           key_states[:, :, :, self.qk_nope_head_dim :] = k_pe

   当然了，如果提供了过去键值缓存，则

           if past_key_value is not None:  # 如果提供了过去键值缓存
               cache_kwargs = {"sin": sin, "cos": cos}  # Specific to RoPE models  # 创建缓存参数
               key_states, value_states = past_key_value.update(
                   key_states, value_states, self.layer_idx, cache_kwargs  # 更新键和值状态
               )

1.6.2 最后做标准注意力相关的计算

如上面提到的

1. 首先，计算attention score
   
2. 然后对V做加权求和，得到attention输出
   
3. 最后，经过矩阵投影，得到MLA的最终输出
   

可知

1. 方法计算查询和键之间的注意力权重 `attn_weights`，并检查其大小是否正确

           attn_weights = (
               # 计算查询和键之间的注意力权重
               torch.matmul(query_states, key_states.transpose(2, 3)) * self.softmax_scale  
           )
   
           # 检查注意力权重的大小是否正确
           if attn_weights.size() != (bsz, self.num_heads, q_len, kv_seq_len):  
               raise ValueError(
                   f"Attention weights should be of size {(bsz, self.num_heads, q_len, kv_seq_len)}, but is"
                   f" {attn_weights.size()}"
               )

2. 如果提供了注意力掩码 `attention_mask`，方法会将其添加到注意力权重中

           assert attention_mask is not None   # 确保注意力掩码不为空
           if attention_mask is not None:      # 如果提供了注意力掩码
               if attention_mask.size() != (bsz, 1, q_len, kv_seq_len):  # 检查注意力掩码的大小是否正确
                   raise ValueError(
                       f"Attention mask should be of size {(bsz, 1, q_len, kv_seq_len)}, but is {attention_mask.size()}"
                   )
               attn_weights = attn_weights + attention_mask              # 将注意力掩码添加到注意力权重中

3. 然后，方法对注意力权重进行归一化和丢弃，计算注意力输出 `attn_output`

           ## 将注意力权重转换为fp32
           attn_weights = nn.functional.softmax(
               # 对注意力权重进行归一化，且将注意力权重转换为查询状态的dtype
               attn_weights, dim=-1, dtype=torch.float32           
           ).to(query_states.dtype) 
   
           attn_weights = nn.functional.dropout(
               # 对注意力权重进行丢弃
               attn_weights, p=self.attention_dropout, training=self.training  
           )
   
           # 计算注意力输出
           attn_output = torch.matmul(attn_weights, value_states)

4. 最后，方法对注意力输出进行线性投影，并根据 `output_attentions` 参数决定是否返回注意力权重

           # 转置注意力输出张量
           attn_output = attn_output.transpose(1, 2).contiguous()  
   
           # 调整注意力输出张量的形状
           attn_output = attn_output.reshape(bsz, q_len, self.num_heads * self.v_head_dim)  
       
           # 对注意力输出进行线性投影
           attn_output = self.o_proj(attn_output)  
   
           if not output_attentions:      # 如果不输出注意力权重
               attn_weights = None          # 将注意力权重设置为None

   参数矩阵 o_proj 的大小 [num_heads * v_head_dim, hidden_size] = [128*128， 5120]

   

5. 方法返回注意力输出、注意力权重和更新后的键值缓存

           # 返回注意力输出、注意力权重和更新后的键值缓存
           return attn_output, attn_weights, past_key_value

第二部分 MLA推理层面的改进：通过矩阵吸收十倍提速 MLA 算子

2.1 MLA算法的回顾与MLA提到的矩阵吸收

2.1.1 对MLA算法的图文公式的再次统一回顾

经过上面的分析，我们已经可以把对应的公式和代码全都一一对应起来

37		对q降维 q_a_proj
38 q		对q升维 q_b_proj
39，q_pe apply_rotary_pos_emb 详见上文的「1.6.1 对查询向量、键向量的旋转位置编码」		q_pe, k_pe = apply_rotary_pos_emb(q_pe, k_pe, cos, sin, position_ids)
40 query_states 同见上文的1.6.1节
41 compressed_kv		降维矩阵 kv_a_proj_with_mqa
42		对k的升维矩阵 kv_b_proj
43 k_pe		q_pe, k_pe = apply_rotary_pos_emb(q_pe, k_pe, cos, sin, position_ids)
44 key_states
45 value_states		对v的升维矩阵 kv_b_proj
46
47 attn_output		参数矩阵 o_proj

有朋友ariesjzj 也把上面公式与代码的逐一对应关系 在V2论文的原图上 直接标注出来了，如下所示

上图左侧有个小的细节值得注意下

• 即在DeepSeek-V2原始论文中， 表示MLA中解耦查询和键的头维度——即旋转维度  上图左侧用的表示
• 至于其他的表示 都一致，比如
  KV压缩维度
  查询压缩维度 
  头的维度表示

2.1.2 如何理解V2论文中针对MLA提到的矩阵吸收

然后重点来了，V2原论文中有这么一段话，即如此文所说

• 其中蓝色框中的向量、需要缓存以进行生成。 在推理过程中，the naive formula需要从中恢复和以进行注意力计算
  where the boxed vectors in blue need to be cached for generation. During inference, the naiveformula needs to recover k𝐶𝑡and v𝐶𝑡from c𝐾𝑉𝑡for attention.
  
  
  
• 幸运的是，由于矩阵乘法的结合律，可
  可将吸收到中
   =>  
  并将吸收到中
   =>  
  因此，不需要为每个查询计算键和值。 通过这种优化，避免了在推理过程中重新计算和的计算开销
  Fortunately, due to the associativelaw of matrix multiplication, we can absorb 𝑊𝑈𝐾into 𝑊𝑈𝑄, and 𝑊𝑈𝑉into 𝑊𝑂.
  Therefore, we do not need to compute keys and values out for each query. Through this optimization, we avoidthe computational overhead for recomputing k𝐶𝑡and v𝐶𝑡during inference

看似轻描淡写的一段话，实则暗藏玄机啊，特别是这句

we can absorb 𝑊𝑈𝐾 into 𝑊𝑈𝑄, and 𝑊𝑈𝑉 into 𝑊𝑂

但，如何理解？

2.2 如何理解absorb 𝑊𝑈𝐾 into 𝑊𝑈𝑄

2.2.1 为何可以吸收以及吸收之后的前后对比

可将吸收到中
 =>  

意味着

• 可将对k做升维的公式42中的
  从而原来的公式42 便没有了
• 吸收到对q做升维的公式38中的
  得到新的公式矩阵
  

上面这个新的公式矩阵即如下图(图源)右上角所示的matrix absorption，而下图左中

• 「如上面介绍到的 V2中 设置的128」维度的，随着将融入进 中
• 便变成了「如上面介绍到的 V2中设置的512」维度的，而这个维度大小与KV的压缩Latent 的维度大小一致

然，问题是，为什么可以这样呢？

原因也很简单

1. 一方面，这两个矩阵、的维度类似
   
   
2. 二方面，咱们有
   
   也就是说我们事实上不需要将低维的展开再计算，而是直接将  通过结合律先和左边做乘法
   而先和左边做乘法的 这个决定，不就相当于将融入进 中了么
   
   也就有了上面所得的
   

而经此一举，可以发现的计算效率得到了明显的改善，如下图所示(图源)

1. 嗯，一般的文章能讲到上面那个程度 便不错了，但 然后呢，然后大家看明白了么？
   可能还是有部分读者没看明白
2. 我写博客时 经常写完一段
   我都会反问我自己 如果把我现在的智商降到原来的1/2，我能否看明白我自己所写的？如果降到1/2能、那降到1/3呢？
   正是因为这种反复的自我反问、自我质疑，让我经常把一篇篇博客修订个不停——而这也是我博客十多年来 一年比一年更受欢迎的重要原因之一

---

so，打破砂锅问到底，咱们再来抠下下面这个公式

即它到底为何要调整计算顺序，它调整计算顺序的意义到底是什么？——截止到25年2月中旬，我个人没看到有文章说的足够详细，故我来好好说明下

从到

1. 后者，可以将两个权重矩阵的乘积预先计算并存储，避免在每次计算注意力权重时重复进行矩阵乘法
   加之前者需分别对  和  计算梯度，而后者可以将二者合并为一个中间矩阵，可以减少梯度计算的分支
   且在有的模型结构中，和的参数可能会直接共享
2. 再进一步分析下 前后复杂度的变化
   
   根据上图左侧 可知
   的维度
   的维度为

   

   而升维矩阵的维度[] ——据此文的2.2.1节，可知
   k的升维矩阵 的维度[]——据此文的2.2.1节，可知
   
   对于前者，咱们拆分成三个子项：两次矩阵乘法、一次点击，具体如下
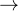
     的矩阵维度是：，复杂度为：
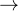
      的矩阵维度是：，复杂度为：
     向量点击的复杂度为：
   故总的复杂度为
   
   其中，实际的主导项为：
   
   同样的，对于后者，咱们也拆分成三个子项：一次矩阵合并 一次矩阵乘法 一次点积，具体如下
     预计算中间矩阵，矩阵维度：，复杂度为：，注意，这个计算仅需一次即可
     计算，向量维度：，复杂度：
     最后乘，向量维度，复杂度：
   
   总复杂度上分为两部分
   首次计算：
   后续每次计算：——一次次复用中间矩阵而已
   
   至此，我再用表格总结一下，可知

   场景	调整前复杂度	调整后复杂度
   单次计算
   第二次到第N次计算（复用）	每次	后续每次

   完美..

2.2.2 对absorb 𝑊𝑈𝐾 into 𝑊𝑈𝑄的coding实现

代码上如何实现呢？为一目了然起见，咱们便来依据下面这个图来一步步coding实现

1. 先对q向量做降维——公式1、然后升维——公式2

           bsz, q_len, _ = hidden_states.size()      # 获取批次大小和查询长度
   
           # 对隐藏状态进行线性投影和归一化，生成查询张量
           q = self.q_b_proj(self.q_a_layernorm(self.q_a_proj(hidden_states)))  
   
           # 调整查询张量的形状
           q = q.view(bsz, q_len, self.num_heads, self.q_head_dim).transpose(1, 2)  

   且过程中涉及到拆解、一部分不带rope：q_nope、一部分带rope：q_pe——公式4

           q_nope, q_pe = torch.split(
               # 将查询张量拆分为不包含位置嵌入的部分和包含位置嵌入的部分
               q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1  
           )

   然后再把kv向量做压缩——公式6、然后切分

           # 对隐藏状态进行线性投影，生成压缩的键值对张量
           compressed_kv = self.kv_a_proj_with_mqa(hidden_states)  
   
           compressed_kv, k_pe = torch.split(
               # 将压缩的键值对张量拆分为不包含位置嵌入的部分和包含位置嵌入的部分
               compressed_kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1  
           )

   这与上面的实现是一致的，不变，相当于降维、切分的过程是不变的，变的是升维，需要从被压缩的空间里 分离出来K、V
2. 所以，据图可知
   
   接下来，清华MadSys Research Group实现了V2原有论文对MLA的这个设计思路：“we can absorb 𝑊𝑈𝐾 into 𝑊𝑈𝑄, and 𝑊𝑈𝑉 into 𝑊𝑂”中的absorb 𝑊𝑈𝐾 into 𝑊𝑈𝑄，有

           # 从 kv_b_proj 中分离的 W^{UK} 和 W^{UV} 两部分，他们要分别在不同的地方吸收
           kv_b_proj = self.kv_b_proj.weight.view(self.num_heads, -1, self.kv_lora_rank)
           q_absorb = kv_b_proj[:, :self.qk_nope_head_dim,:]
           out_absorb = kv_b_proj[:, self.qk_nope_head_dim:, :]

   然后对q_pe单独做rope——对应上图右侧的公式4

           cos, sin = self.rotary_emb(q_pe)
           q_pe = apply_rotary_pos_emb(q_pe, cos, sin, q_position_ids)

3. 接下来，如公式3所述

           # !!! 关键点，W^{UK} 即 q_absorb 被 q_nope 吸收
           q_nope = torch.einsum('hdc,bhqd->bhqc', q_absorb, q_nope) 

   咱们来梳理一下维度变化
   
   如ZHANG Mingxing等人在此文中所说
   q_nope = torch.einsum('hdc,bhqd->bhqc', q_absorb, q_nope) 中
   q_absorb 的维度是 [head_num, q_head_dim, kv_lora_rank]，分别代表着头的个数、头维度、kv_lora_rank的维度
   q_nope 是 [batch_size, head_num, q_len, q_head_dim]，分别代表着batch大小、头的个数、q的长度、头的维度
   
   相当于做了一个将每个 head 的维度从
   q_head_dim ——如上图左中的所示，V2中设置的128维
   投影到 kv_lora_rank ——如下图左中的，V2中设置的512维 所示的 BMM
   
   
   最后则是

           # 吸收后 attn_weights 直接基于 compressed_kv 计算不用展开
           attn_weights = torch.matmul(q_pe, k_pe.transpose(2, 3)) + torch.einsum('bhqc,blc->bhql', q_nope, compressed_kv)
           attn_weights *= self.softmax_scale

   如ZHANG Mingxing等人在此文中所说
   torch.einsum('bhqc,blc->bhql', q_nope, compressed_kv) 中更新后的
   q_nope 的维度是 [batch_size, head_num, q_len, kv_lora_rank]
   compressed_kv 是 [batch_size, past_len, kv_lora_rank]
   
   由于不同 head 的 q_nope 部分 share 了共同的 compressed_kv 部分，实际计算的是 batch_size 个 [head_num * q_len, kv_lora_rank] 和 [past_len, kv_lora_rank] 的矩阵乘法。计算等价于一个 MQA 操作，计算强度正比于 head_num 的也就是 128
   因此相比 MHA，吸收后的 MLA 计算强度要大得多，因此也可以更加充分的利用 GPU 算力

2.3 如何理解𝑊𝑈𝑉 into 𝑊𝑂

2.3.1 为何可以吸收及吸收前后的对比

并将吸收到中
 =>  

意味着

• 将对 v 做升维的公式45中的
  从而原来的公式45 便没有了
• 吸收到公式47中的参数矩阵
  得到新的公式矩阵
  

即如下图右下角所示的matrix absorption，而下图左上角所示的(10,11)便是这个将吸收到中的过程

2.3.2 原始顺序下的注意力计算及coding实现

同样的，经此一举，下述注意力计算过程的第3步

1.  
2. 
3. 

得到了明显的改善，如下图所示(图源)

上图左侧相当于是

先提前说下各个输入张量的维度如下：

• c_t_KV: (batch, seq_len, channel)，即 (b, l, c)，分别代表batch、序列长度、通道数
• W_UV: (num_heads, head_dim, channel)，即 (h, d, c)，分别代表头数、头维度、通道数
• attn_weights: (batch, query_len, num_heads, seq_len)，即 (b, q, h, l)，分别代表batch、查询长度、头数、序列长度
• W_o: (num_heads, head_dim, output_dim)，即 (h, d, D)

1. 第一步，计算值向量(以下两种表达方式，是完全同一个意思)
   
   
   将权重矩阵​ 作用于输入序列 ​，生成每个位置  和头  对应的值向量 ，相当于对每个位置 ，生成每个头 h 对应的值向量（维度 d）
   
   对应的代码为

   v_t = einsum('hdc,blc->blhd', W_UV, c_t_KV)

2. 第二步，计算注意力加权输出
   
   
   通过注意力权重 attn_weightsattn_weights 对值向量 ​ 加权求和，得到每个查询位置  和头  的输出 
   相当于对每个查询位置 ，聚合所有序列位置  的值向量
   
   对应的代码为

   o = einsum('bqhl,blhd->bqhd', attn_weights, v_t)

3. 第三步，线性投影得到最终输出 u
   
   
   将输出  通过权重矩阵 ​ 投影到最终维度 ，并跨所有查询位置  求和，相当于对每个头 h，将多个查询位置 q 的结果聚合到输出维度 D
   
   对应的代码为

   u = einsum('hdD,bhqd->bhD', W_o, o)

将上面的三个步骤合并为一个操作，就是

对应的代码为

u = einsum('hdc,blc,bqhl,hdD->bhD', W_UV, c_t_KV, attn_weights, W_o)

2.3.3 MadSys利用结合律后的注意力计算顺序及coding实现

下图右侧相当于是

1. 第一步，先计算注意力加权上下文 o
   
   先通过注意力权重加权输入序列​，生成上下文表示，相当于对每个头 h 和查询位置 q，生成一个聚合后的上下文表示
   
   对应的代码为

   o_ = einsum('bhql,blc->bhqc', attn_weights, c_t_KV)

2. 第二步：应用值投影矩阵
   
   将上下文表示 通过 ​ 投影到目标维度 ，相当于每个头 h 和查询位置 q 对应一个值向量
   
   对应的代码为

   o = einsum('bhqc,hdc->bhqd', o_, W_UV)

3. 第三步，线性投影得到最终输出 u（与原始第三步相同）
   
   最终投影到 ，跨所有查询位置  求和，相当于对每个头 h，将多个查询位置 q 的结果聚合到输出维度 D
   
   对应的代码为

   u = einsum('hdD,bhqd->bhD', W_o, o)

2.3.4 是否结合乘法结合律的差异对比

我用下面这个表格来说明，为何要通过乘法结合律改变计算顺序

	原始计算顺序	通过乘法结合律调整计算顺序
第一步及其代价	生成值向量 v_t：维度 (b, l, h, d)	先聚合输入序列 c_t_KV：生成中间结果 o_，维度 (b, h, q, c)
	代价是：中间张量 v_t 的维度是 (b, l, h, d)——各个维度分别代表(batch、序列长度、头数、头维度) 如果序列长度 l 很大（例如长文本处理），存储 v_t 会占用大量内存	代价是：新中间结果 o_ 的维度为 (b, h, q, c)——各个维度分别代表(batch、头数、查询长度、通道数) 如果 通道数c < 头维度d 或 查询长度q < 序列长度l（常见于某些注意力模式），则 o_ 的内存占用显著小于 v_t
第二步	注意力加权求和 o：维度 (b, q, h, d)	投影到值空间 o：维度 (b, h, q, d)
第三步	输出投影 u：维度 (b, h, D)	输出投影 u：维度 (b, h, D)

通过上面这个我总结的表格，可以一目了然的看到，前后两种顺序的内存占用对比

步骤	原始方法中间变量维度	优化后中间变量维度
中间结果	v_t: (b, l, h, d)	o_: (b, h, q, c)
内存占用	O(b·l·h·d)	O(b·h·q·c)

从而也就有了：如果 q < l（例如，查询长度小于序列长度）且 c ≈ d(比如可能都设置的64)，优化后的内存占用更低，而这对于处理 长序列（如 l=4096）至关重要，可避免内存溢出OOM

至此，我总算不厌其烦、足够耐心的说清楚这个问题了，至于完整的代码见「七月在线」官网首页的DeepSeek项目实战营..

且目前为止，​我把deepseek的三大算法创新，GRPO、MLA、MTP背后的理论及代码实现——​​我全都写清楚了，grpo代码解析的TRL中的，mla代码解析的v2官方的，mtp的代码 解析的我自己实现的