-正在学习OPENGL阅读了Twinsen编写的技术博客,收益颇多,特此转载
http://blog.csdn.net/popy007/article/details/1797121
透视投影是3D固定流水线的重要组成部分,是将相机空间中的点从视锥体(frustum)变换到规则观察体(Canonical View Volume)中,待裁剪完毕后进行透视除法的行为。在算法中它是通过透视矩阵乘法和透视除法两步完成的。
透视投影变换是令很多刚刚进入3D图形领域的开发人员感到迷惑乃至神秘的一个图形技术。其中的理解困难在于步骤繁琐,对一些基础知识过分依赖,一旦对它们中的任何地方感到陌生,立刻导致理解停止不前。
没错,主流的3D APIs如OpenGL、D3D的确把具体的透视投影细节封装起来,比如
gluPerspective(…)就可以根据输入生成一个透视投影矩阵。而且在大多数情况下不需要了解具体的内幕算法也可以完成任务。但是你不觉得,如果想要成为一个职业的图形程序员或游戏开发者,就应该真正降伏透视投影这个家伙么?我们先从必需的基础知识着手,一步一步深入下去(这些知识在很多地方可以单独找到,但我从来没有在同一个地方全部找到,但是你现在找到了J)。
我们首先介绍两个必须掌握的知识。有了它们,我们才不至于在理解透视投影变换的过程中迷失方向(这里会使用到向量几何、矩阵的部分知识,如果你对此不是很熟悉,可以参考《向量几何在游戏编程中的使用》系列文章)。
齐次坐标表示
透视投影变换是在齐次坐标下进行的,而齐次坐标本身就是一个令人迷惑的概念,这里我们先把它理解清楚。
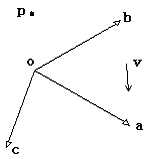
根据《向量几何在游戏编程中的使用6》中关于基的概念。对于一个向量v以及基oabc,
可以找到一组坐标(v1,v2,v3),使得
v = v1 a + v2 b + v3 c (1)
而对于一个点p,则可以找到一组坐标(p1,p2,p3),使得
p – o = p1 a + p2 b + p3 c (2)
从上面对向量和点的表达,我们可以看出为了在坐标系中表示一个点(如p),我们把点的位置看作是对这个基的原点o所进行的一个位移,即一个向量——p – o(有的书中把这样的向量叫做位置向量——起始于坐标原点的特殊向量),我们在表达这个向量的同时用等价的方式表达出了点p:
p = o + p1 a + p2 b + p3 c (3)
(1)(3)是坐标系下表达一个向量和点的不同表达方式。这里可以看出,虽然都是用代数分量的形式表达向量和点,但表达一个点比一个向量需要额外的信息。如果我写出一个代数分量表达(1, 4, 7),谁知道它是个向量还是个点!
我们现在把(1)(3)写成矩阵的形式:
这里(a,b,c,o)是坐标基矩阵,右边的列向量分别是向量v和点p在基下的坐标。这样,向量和点在同一个基下就有了不同的表达:3D向量的第4个代数分量是0,而3D点的第4个代数分量是1。像这种这种用4个代数分量表示3D几何概念的方式是一种齐次坐标表示。
“齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换。”—— F.S. Hill, JR
这样,上面的(1, 4, 7)如果写成(1,4,7,0),它就是个向量;如果是(1,4,7,1),它就是个点。
下面是如何在普通坐标(Ordinary Coordinate)和齐次坐标(Homogeneous Coordinate)之间进行转换:
从普通坐标转换成齐次坐标时,
如果(x,y,z)是个点,则变为(x,y,z,1);
如果(x,y,z)是个向量,则变为(x,y,z,0)
从齐次坐标转换成普通坐标时,
如果是(x,y,z,1),则知道它是个点,变成(x,y,z);
如果是(x,y,z,0),则知道它是个向量,仍然变成(x,y,z)
以上是通过齐次坐标来区分向量和点的方式。从中可以思考得知,对于平移T、旋转R、缩放S这3个最常见的仿射变换,平移变换只对于点才有意义,因为普通向量没有位置概念,只有大小和方向,这可以通过下面的式子清楚地看出:
而旋转和缩放对于向量和点都有意义,你可以用类似上面齐次表示来检测。从中可以看出,齐次坐标用于仿射变换非常方便。
此外,对于一个普通坐标的点P=(Px, Py, Pz),有对应的一族齐次坐标(wPx, wPy, wPz, w),其中w不等于零。比如,P(1, 4, 7)的齐次坐标有(1, 4, 7, 1)、(2, 8, 14, 2)、(-0.1, -0.4, -0.7, -0.1)等等,这个其次坐标表示的仍然是P(1, 4, 7)。因此,如果把一个点从普通坐标变成齐次坐标,给x,y,z乘上同一个非零数w,然后增加第4个分量w;如果把一个齐次坐标转换成普通坐标,把前三个坐标同时除以第4个坐标,然后去掉第4个分量。由此可推测4*4矩阵中最后一个数值,可以使点发生整体比列变化。比如:此值为2,则其余的值和单位矩阵一样,则变化后此点变为P'=(Px, Py, Pz,2),按照齐次坐标的规则P'=(Px/2, Py/2, Pz/2).
由于齐次坐标使用了4个分量来表达3D概念,使得平移变换可以使用矩阵进行,从而如F.S. Hill, JR所说,仿射(线性)变换的进行更加方便。由于图形硬件已经普遍地支持齐次坐标与矩阵乘法,因此更加促进了齐次坐标使用,使得它似乎成为图形学中的一个标准。
简单的线性插值
这是在图形学中普遍使用的基本技巧,我们在很多地方都会用到,比如2D位图的放大、缩小,Tweening变换,以及我们即将看到的透视投影变换等等。基本思想是:给一个x属于[a, b],找到y属于[c, d],使得x与a的距离比上ab长度所得到的比例,等于y与c的距离比上cd长度所得到的比例,用数学表达式描述很容易理解:
这样,从a到b的每一个点都与c到d上的唯一一个点对应。有一个x,就可以求得一个y。
此外,如果x不在[a, b]内,比如x < a或者x > b,则得到的y也是符合y < c或者y > d,比例仍然不变,插值同样适用。
透视投影变换
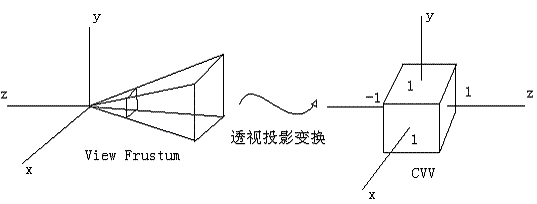
好,有了上面两个理论知识,我们开始分析这次的主角——透视投影变换。这里我们选择OpenGL的透视投影变换进行分析,其他的APIs会存在一些差异,但主体思想是相似的,可以类似地推导。经过相机矩阵的变换,顶点被变换到了相机空间(可以认为此时的顶点坐标(视点矩阵乘以初始顶点坐标生成的新坐标)对应视点坐标系)。这个时候的多边形也许会被视锥体裁剪,但在这个不规则的体中进行裁剪并非那么容易的事情,所以经过图形学前辈们的精心分析,裁剪被安排到规则观察体(Canonical View Volume, CVV)中进行,CVV是一个正方体,x, y, z的范围都是[-1,1],多边形裁剪就是用这个规则体完成的。所以,事实上是透视投影变换由两步组成:
1) 用透视变换矩阵把顶点从视锥体中变换到裁剪空间的CVV中。
2) CVV裁剪完成后进行透视除法(一会进行解释)。
我们一步一步来,我们先从一个方向考察投影关系。
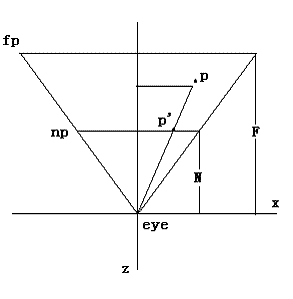
上图是右手坐标系中顶点在相机空间中的情形。设P(x,z)是经过相机变换之后的点,视锥体由eye——眼睛位置,np——近裁剪平面,fp——远裁剪平面组成。N是眼睛到近裁剪平面的距离,F是眼睛到远裁剪平面的距离。投影面可以选择任何平行于近裁剪平面的平面,这里我们选择近裁剪平面作为投影平面。设P’(x’,z’)是投影之后的点,则有z’ = -N。通过相似三角形性质,我们有关系:
同理,有
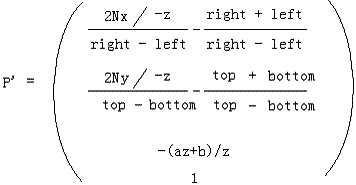
这样,我们便得到了P投影后的点P’
从上面可以看出,投影的结果z’始终等于-N,在投影面上。实际上,z’对于投影后的P’已经没有意义了,这个信息点已经没用了。但对于3D图形管线来说,为了便于进行后面的片元操作,例如z缓冲消隐算法,有必要把投影之前的z保存下来,方便后面使用。因此,我们利用这个没用的信息点存储z,处理成:
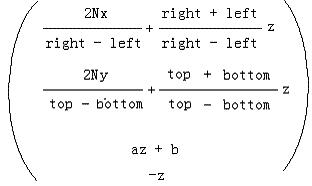
这个形式最大化地使用了3个信息点,达到了最原始的投影变换的目的,但是它太直白了,有一点蛮干的意味,我感觉我们最终的结果不应该是它,你说呢?我们开始结合CVV进行思考,把它写得在数学上更优雅一致,更易于程序处理。假入能够把上面写成这个形式:
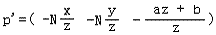
那么我们就可以非常方便的用矩阵以及齐次坐标理论来表达投影变换:
其中
哈,看到了齐次坐标的使用,这对于你来说已经不陌生了吧?这个新的形式不仅达到了上面原始投影变换的目的,而且使用了齐次坐标理论,使得处理更加规范化。注意在把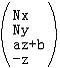
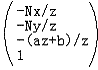
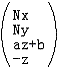
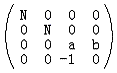
矩阵
就是我们投影矩阵的第一个版本。你一定会问为什么要把z写成
有两个原因:
1) P’的3个代数分量统一地除以分母-z,易于使用齐次坐标变为普通坐标来完成,使得处理更加一致、高效。
2) 后面的CVV是一个x,y,z的范围都为[-1,1]的规则体,便于进行多边形裁剪。而我们可以适当的选择系数a和b,使得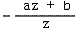
接下来我们就求出a和b:
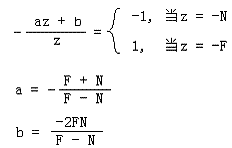
这样我们就得到了透视投影矩阵的第一个版本:
使用这个版本的透视投影矩阵可以从z方向上构建CVV,但是x和y方向仍然没有限制在[-1,1]中,我们的透视投影矩阵的下一个版本就要解决这个问题。
为了能在x和y方向把顶点从Frustum情形变成CVV情形,我们开始对x和y进行处理。先来观察我们目前得到的最终变换结果:
我们知道-Nx / z的有效范围是投影平面的左边界值(记为left)和右边界值(记为right),即[left, right],-Ny / z则为[bottom, top]。而现在我们想把-Nx / z属于[left, right]映射到x属于[-1, 1]中,-Ny / z属于[bottom, top]映射到y属于[-1, 1]中。你想到了什么?哈,就是我们简单的线性插值,你都已经掌握了!我们解决掉它:
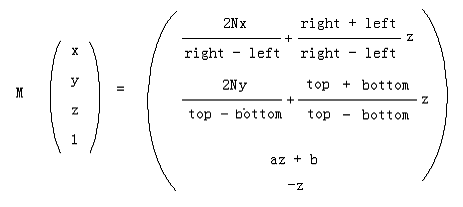
则我们得到了最终的投影点:
下面要做的就是从这个新形式出发反推出下一个版本的透视投影矩阵。注意到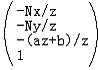
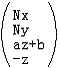
而这个结果又是这么来的:
则我们最终得到:
M就是最终的透视变换矩阵。相机空间中的顶点,如果在视锥体中,则变换后就在CVV中。如果在视锥体外,变换后就在CVV外。而CVV本身的规则性对于多边形的裁剪很有利。OpenGL在构建透视投影矩阵的时候就使用了M的形式。注意到M的最后一行不是(0 0 0 1)而是(0 0 -1 0),因此可以看出透视变换不是一种仿射变换,它是非线性的。另外一点你可能已经想到,对于投影面来说,它的宽和高大多数情况下不同,即宽高比不为1,比如640/480。而CVV的宽高是相同的,即宽高比永远是1。这就造成了多边形的失真现象,比如一个投影面上的正方形在CVV的面上可能变成了一个长方形。解决这个问题的方法就是在对多变形进行透视变换、裁剪、透视除法之后,在归一化的设备坐标(Normalized Device Coordinates)上进行的视口(viewport)变换中进行校正,它会把归一化的顶点之间按照和投影面上相同的比例变换到视口中,从而解除透视投影变换带来的失真现象。进行校正前提就是要使投影平面的宽高比和视口的宽高比相同。
关于失真问题:进行校正前提就是要使投影平面的宽高比和视口的宽高比相同。
是不是只要当一个3D物体的投影完全覆盖了投影平面时才会产生失真问题?
不是这样。图像比例的转换步骤为:
projection plane => CVV => viewport
这里CVV的是恒为1:1的,因此,你只有让projection plane(PP)的比例和viewport(VP)的比例相同,才能保证不失真。比如,一个PP中的物体的宽高是4x3,而PP的宽高是40x30,比例是4:3,则进入CVV之后,物体的宽高变成了1x1,这明显失真了(物体变瘦了)。再从CVV进入VP,如果VP的宽高也是1x1,比例1:1,则物体也会变成1x1(失真)。但如果VP也是4:3,那么从CVV进入VP后又会变回原来的尺寸4x3,这就解除了CVV的失真。
便利的投影矩阵生成函数
3D APIs都提供了诸如gluPerspective(fov, aspect, near, far)或者D3DXMatrixPerspectiveFovLH(pOut, fovY, Aspect, zn, zf)这样的函数为用户提供快捷的透视矩阵生成方法。我们还是用OpenGL的相应方法来分析它是如何运作的。
gluPerspective(fov, aspect, near, far)
fov即视野,是视锥体在xz平面或者yz平面的开角角度,具体哪个平面都可以。OpenGL和D3D都使用yz平面。
aspect即投影平面的宽高比。
near是近裁剪平面的距离
far是远裁剪平面的距离。
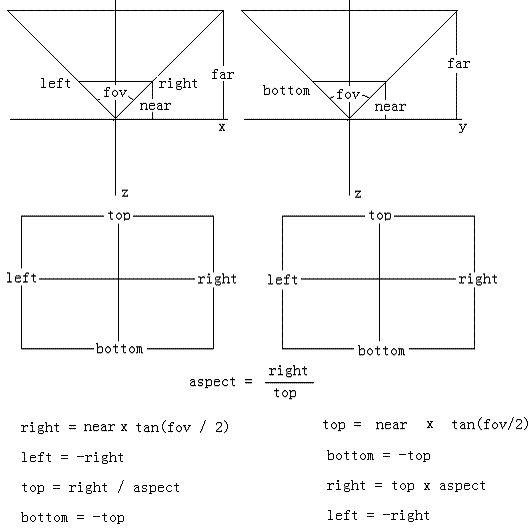
上图中左边是在xz平面计算视锥体,右边是在yz平面计算视锥体。可以看到左边的第3步top = right / aspect使用了除法(图形程序员讨厌的东西),而右边第3步right = top x aspect使用了乘法,这也许就是为什么图形APIs采用yz平面的原因吧!
到目前为止已经完成了对透视投影变换的阐述,我想如果你一直跟着我的思路下来,应该能够对透视投影变换有一个细节层次上的认识。当然,很有可能你已经是一个透视投影变换专家,如果是这样的话,一定给我写信,指出我认识上的不足,我会非常感激J。Bye!
关于上面中的一些疑问:
1. 为什么要把z写成(za+b)/z,你说了两个原因,第一个我了解了,第二个,你说为了方便进行多边形剪裁,怎么方便啦! 为什么是za+b呢?你为什么不写成其它的形式呢?
解答:已知: z (点p在z轴上的值)
目标: z‘ (深度信息 -1~+1)
原始问题就转化为,怎么在已知点p的z坐标的情况下,求得用在深度测试中的z’
透视投影中z‘与z之间为非线性关系 —— z‘z = az +b
(PS:正交投影中z’与z为线性关系—— z’ = az + b)
那你肯定要问: (1) 为什么正交投影中z‘和z为线性关系 (2)为什么透视投影不能和正交投影一样都采用线性关系
如果理解了这两个问题,那么就解决你的疑问了~~~
关于(1): 正交投影的实质就是 将Frustum的中心先平移到eye坐标系原点,然后再缩放至CVV。x,y,z三轴均是如此,而对z平移和缩放不就是 z’ = az + b吗?为线性关系 ^_^解决
关于(2): 透视投影没有这么简单粗暴,x‘和y’不是简单的平移和缩放就能搞定,x‘ = -Nx/z; y'= -Ny/z,即 x’和x,y'和y不是线性关系,均与z有关。但是注意,此时z‘和z仍可以写成线性关系z’ = az+b,因为透视投影跟正交投影不同的地方只是影响x‘,y’的计算,那为什么z‘也要采取z’z = az+b的非线性关系呢?因为,要少数服从多数啊~~~ ^_^
如果现在你还没有清楚,那是正常的,因为还有一个关键的东西需要理解!
重要: 矩阵*向量 只能模拟线性关系的处理 @###@
所以对于 x‘ = -Nx/z; y'= -Ny/z 必须要先用 矩阵*向量 得到线性关系 x‘ = -Nx; y'= -Ny,然后同时除以z才能得到最终结果 x‘ = -Nx/z; y'= -Ny/z。
记住x,y,z三个轴地位等价,所以处理过程肯定是相同的,对z而言,也需要先用 矩阵*向量 得到线性关系 z’ = az+b (公式1),然后再除以z得到最终结果 z‘ = a + b/z, 即得到z‘和z的非线性关系式 z’z = az + b
现在又有问题了,凭什么 公式1 要这样写,线性关系 z‘= az 或者z' = b为什么不行? 当然啦。要保证方程组 z=N时,z'=-1;z=F时,z'=1有解就必须要 z’ = a + b/z。 z‘= az 和z' = b均是无解! ^_^ 解决。其实还有一个重要的原因:也是我后来研究透视纹理映射才得到的结论。那就是,z和z'也非线性关系,和透视纹理映射一样,是z'=a(1/z)+b的关系,也就是说z'和1/z是线性关系。因此就是z'=(az+b)/z的关系。具体的推论可以参考我的透视纹理映射的文章;
2. 透视裁剪是在透视除法之前做的还是之后做的? 如果是在之前做的,裁剪的依据是判断在[-z, z]之内吗?
如果是在之后我们知道是判断[-1,1]。之前和之后有什么差别吗?
以下是网友之间的对话和解答:
Q:因為一般討論轉換矩陣和裁剪的關係著墨實在太少了,直覺上認為轉換矩陣的功能就只在空間變換和投影上,我也不是沒想過在透視除法前做裁剪,但以為要另外做處理,須另外提供裁剪邊界相關訊息,沒想到裁剪平面的訊息就隱藏在矩陣中
A:个人认为为什么在透视除法前做裁剪:
1:透视除法前能做裁剪:做法:
1.1:判定阶段:如果-w<x<w,-w<y<w,-w<z<w。那么这一点就在CVV中。
1.2:计算阶段:如果线段AB需要裁剪,计算新点:
t=-(Xa+Wa)/((Xb+Wb)-(Xa+Wa))(对于-w裁剪)
Xnew=Xa+t(Xb-Xa).
此处应该不是正确的解释,因为即使进入CVV中,[-1, 1]内也可以计算新的点。只不过这个时候做,还有一个解释是因为此时时浮点,小数少,精度会准确。
所以在除法前完全能做。
2:为什么在除法前做:因为除法是很费时的,在除法前剔除一些顶点,对于除法来说能减少不少时间。
综上所述:既然裁剪在除法之前能做,又能节约时间,那为什么不在除法之前做呢???对吧。。
一个3D物体有的点可能z值为0. z为0的点是肯定没有意义的,绝对可以剔除。因为近平面不可能为 z=0,所以z轴坐标为0的点p不可能存在于投影视椎体里。这样进行透视除法时就不会出现问题。
另外的解释:opengl在进行裁剪的时候使用的是未经透视除法的齐次坐标形式,在这个形式的基础上进行裁剪比较方便(主要是可以留住原始的z值,并且在CVV裁剪的时候随时可以用x,y,z除以w得到CVV中的值)。而裁剪完毕之后呢,才会真正的使用透视除法把齐次形式变成普通形式。在外部看来,实际上可以理解为裁剪和透视除法是一步完成的,但具体来看就是我上面所说那样的。
注意:有一次问原文博主,他说:是在透视除法之后做的。否则cvv就没有存在的必要,用cvv裁剪就是因为它规则。所以就有点蒙了,不过无关紧要。
3。 投影矩阵为什么是左乘当前矩阵
没这回事:)对一个点P的变换是:
“P x 模型矩阵 x 视图矩阵 x 投影矩阵” 或者
"投影矩阵 x 视图矩阵 x 模型矩阵 x P"
两种方式分别对应左右两种坐标系。没有其他的顺序。
意义都是一样的,都是点!只不过是一个行向量表示,一个列向量表示。用哪一个完全是习惯问题。
右手坐标系:用列向量表示点;左手坐标系:行向量表示点
对与右手坐标系,之所以投影矩阵放在最前面,是因为投影变换是最后面执行的变换







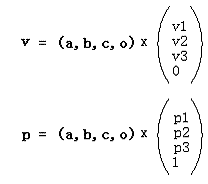
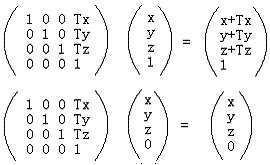
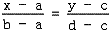
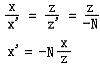
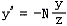
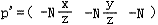
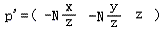
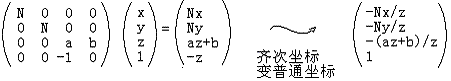
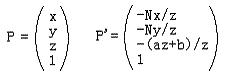
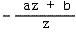
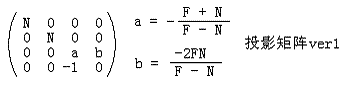
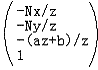

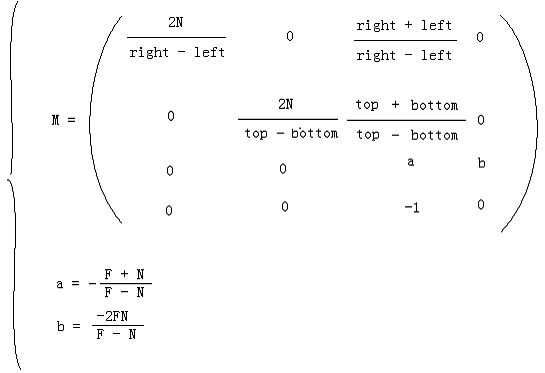














 4981
4981

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








